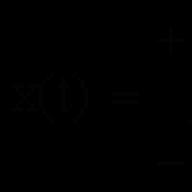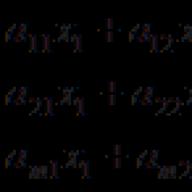di mana ada beberapa angka (beberapa atau bahkan semua angka ini mungkin nol). Ini berarti persamaan berikut ada di antara elemen kolom:

atau , .

Ini mengikuti dari (3.3.1) itu

(3.3.2)

dimana garis nol.

Definisi. Baris matriks A bergantung secara linier jika ada bilangan yang tidak semuanya sama dengan nol pada saat yang sama

(3.3.3)

Jika persamaan (3.3.3) benar jika dan hanya jika, maka baris tersebut disebut bebas linier. Relasi (3.3.2) menunjukkan bahwa jika salah satu baris diekspresikan secara linier dalam hal yang lain, maka baris tersebut bergantung secara linier.

Mudah untuk melihat kebalikannya: jika garis-garis itu bergantung secara linear, maka ada garis yang akan menjadi kombinasi linear dari garis-garis lainnya.

Misalkan, dalam (3.3.3), lalu .

Definisi. Biarkan minor tertentu dibedakan dalam matriks Ar -th order dan biarkan minor (r +1) urutan matriks yang sama seluruhnya berisi minor. Katakanlah dalam kasus ini minor berbatasan dengan minor (atau merupakan perbatasan untuk).

Kami sekarang membuktikan lemma penting.

Kata pengantar singkat tentang membatasi anak di bawah umur. Jika pesanan kecilr dari matriks A \u003d adalah bukan nol, dan semua anak di bawah umur yang berbatasan dengannya sama dengan nol, maka setiap baris (kolom) matriks A adalah kombinasi linier dari baris (kolom) yang menyusunnya.

Bukti. Tanpa kehilangan generalitas penalaran, kita akan berasumsi bahwa minor bukan nolr Urutan ke -th ada di pojok kiri atas matriks A \u003d:

Untuk k pertama dari baris matriks A, pernyataan lemma sudah jelas: cukup memasukkan baris yang sama dengan koefisien yang sama dengan satu dalam kombinasi linier, dan sisanya - dengan koefisien sama dengan nol.

Sekarang, mari kita buktikan bahwa baris-baris matriks A yang tersisa diekspresikan secara linier dalam baris pertamak garis. Untuk melakukan ini, buat minor (r +1) urutan dengan menambahkan minorbaris k () dan lkolom ke ():

Minor yang dihasilkan adalah nol untuk semuak dan l ... Jika, maka sama dengan nol karena mengandung dua kolom identik. Jika, maka minor yang dihasilkan adalah minor yang berbatas untuk dan, oleh karena itu, sama dengan nol menurut hipotesis lemma.

Mari kita kembangkan minor dengan elemen-elemen yang terakhirlkolom ke:

(3.3.4)

di mana aljabar melengkapi elemen-elemennya. Oleh karena itu, komplemen aljabar merupakan matriks minor dari A. Bagi (3.3.4) dengan dan ekspresikan melalui:

(3.3.5)

dimana,.

Dengan asumsi kita mendapatkan:

(3.3.6)

Ekspresi (3.3.6) artinyak baris ke-dari matriks A diekspresikan secara linier dalam baris pertamar garis.

Karena ketika matriks ditransposisikan, nilai minornya tidak berubah (karena sifat determinan), maka semua yang telah dibuktikan juga berlaku untuk kolom. Teorema tersebut terbukti.

Akibat wajar I ... Setiap baris (kolom) dari matriks adalah kombinasi linier dari baris dasarnya (kolom). Memang, basis minor dari matriks adalah bukan nol, dan semua minor yang berbatasan dengannya sama dengan nol.

Akibat wajar II. Determinan n -th order jika dan hanya jika sama dengan nol ketika itu berisi baris (kolom) dependen linier. Kecukupan ketergantungan linier dari baris (kolom) untuk persamaan determinan ke nol telah dibuktikan sebelumnya sebagai properti dari determinan.

Mari kita buktikan kebutuhannya. Biarkan matriks persegi diberikann -th order, satu-satunya minor adalah nol. Oleh karena itu dapat disimpulkan bahwa peringkat matriks ini kurang darin , yaitu setidaknya ada satu baris yang merupakan kombinasi linier dari baris basis matriks ini.

Mari kita buktikan satu teorema lagi tentang pangkat sebuah matriks.

Dalil. Jumlah maksimum baris independen linier dari sebuah matriks sama dengan jumlah maksimum kolom independen liniernya dan sama dengan peringkat matriks ini.

Bukti. Misalkan peringkat matriks A \u003d menjadir. Lalu ada k string dasar bersifat bebas linier, jika tidak basis minor akan menjadi nol. Di sisi lain, apa sajar +1 atau lebih garis bergantung secara linier. Dengan asumsi sebaliknya, kita dapat menemukan pesanan kecil lebih darir berbeda dari nol oleh akibat wajar 2 dari lemma sebelumnya. Yang terakhir ini bertentangan dengan fakta bahwa urutan maksimum dari anak di bawah umur bukan nol adalahr ... Semua yang telah kami buktikan untuk baris juga berlaku untuk kolom.

Sebagai kesimpulan, kami menyajikan satu metode lagi untuk menemukan peringkat matriks. Pangkat matriks dapat ditentukan dengan mencari minor bukan nol dari urutan maksimum.

Pada pandangan pertama, ini membutuhkan penghitungan, meskipun terbatas, tetapi kemungkinan sangat besar jumlah minor dari matriks ini.

Teorema berikut, bagaimanapun, memungkinkan kita untuk membuat penyederhanaan yang signifikan dalam hal ini.

Dalil. Jika minor dari matriks A adalah bukan nol, dan semua minor yang berbatasan dengannya sama dengan nol, maka peringkat matriks tersebut adalahr.

Bukti. Ini cukup untuk menunjukkan bahwa setiap subsistem baris dari matriks untukS\u003e r akan bergantung secara linier di bawah kondisi teorema (ini akan menyiratkan bahwa r adalah jumlah maksimum baris bebas linier dari matriks atau salah satu minornya yang berurutan lebih besar darik sama dengan nol).

Misalkan sebaliknya. Biarkan baris menjadi bebas linier. Menurut lemma tentang anak di bawah umur yang berbatasan, masing-masing akan diekspresikan secara linier dalam bentuk garis di mana ada minor dan yang, karena berbeda dari nol, tidak bergantung secara linier:

(3.3.7)

Pertimbangkan matriks K dari koefisien ekspresi linier (3.3.7):

Baris-baris dari matriks ini dilambangkan dengan ... Mereka akan bergantung secara linier, karena peringkat dari matriks K, yaitu. jumlah maksimum garis bebas liniernya tidak melebihir< S ... Oleh karena itu, ada bilangan, tidak semuanya sama dengan nol, itu

Mari kita lanjutkan ke persamaan komponen

(3.3.8)

Sekarang perhatikan kombinasi linier berikut:

atau

Pertimbangkan matriks mxn A. yang sewenang-wenang, tidak harus persegi.

Peringkat matriks.

Konsep pangkat suatu matriks dikaitkan dengan konsep ketergantungan linier (independensi) baris (kolom) suatu matriks. Mari pertimbangkan konsep string ini. Untuk kolom - sama.

Mari kita tunjukkan sink matriks A:

e 1 \u003d (a 11, a 12, ..., a 1n); е 2 \u003d (а 21, а 22, ..., а 2n); ..., е m \u003d (а m1, а m2, ..., а mn)

e k \u003d e s jika a kj \u003d a sj, j \u003d 1,2,…, n

Operasi aritmatika pada baris matriks (penjumlahan, perkalian dengan bilangan) diperkenalkan sebagai operasi yang dilakukan elemen demi elemen: λе k \u003d (λа k1, λа k2,…, λа kn);

e k + e s \u003d [(a k1 + a s1), (a k2 + a s2),…, (a kn + a sn)].

Baris e dipanggil kombinasi linear baris e 1, e 2, ..., e k, jika sama dengan jumlah produk dari baris ini dengan bilangan real acak:

е \u003d λ 1 е 1 + λ 2 е 2 +… + λ k е k

Baris e 1, e 2, ..., e m disebut bergantung secara linier, jika ada bilangan real λ 1, λ 2,…, λ m, tidak semuanya sama dengan nol, maka kombinasi linier baris-baris ini sama dengan baris nol: λ 1 е 1 + λ 2 е 2 +… + λ m е m \u003d 0 ,Dimana 0 =(0,0,…,0) (1)

Jika kombinasi linier sama dengan nol jika dan hanya jika semua koefisien λ i sama dengan nol (λ 1 \u003d λ 2 \u003d… \u003d λ m \u003d 0), maka baris e 1, e 2, ..., e m disebut independen linier.

Teorema 1... Untuk garis e 1, e 2,…, e m menjadi dependen linier, itu perlu dan cukup bahwa salah satu dari baris ini menjadi kombinasi linier dari baris yang tersisa.

Bukti. Perlu... Misalkan baris e 1, e 2,…, e m bergantung secara linier. Biarkan, untuk kepastian, masuk (1) λ m ≠ 0, lalu

Begitu string e m adalah kombinasi linier dari string lainnya. Ch.d.

Kecukupan... Misalkan salah satu garis, misalnya e m, menjadi kombinasi linier dari sisa garis. Lalu ada angka yang dipegang persamaan, yang dapat ditulis ulang sebagai,

di mana setidaknya 1 dari koefisien, (-1), bukan nol. Itu. string bergantung secara linier. Ch.d.

Definisi. Kecil dari urutan ke-k dari matriks A dengan ukuran mxn disebut determinan orde k dengan elemen yang terletak di perpotongan setiap k baris dan k kolom apa pun dari matriks A. (k≤min (m, n)). ...

Contoh., anak di bawah umur dari urutan pertama: \u003d, \u003d;

urutan ke-2 di bawah umur :, urutan ke-3

Matriks urutan ke-3 memiliki 9 anak urutan ke-1, 9 anak di bawah umur urutan ke-2, dan 1 anak urutan ke-3 (penentu matriks ini).

Definisi. Peringkat matriks A adalah urutan tertinggi dari anak di bawah umur bukan nol dari matriks ini. Sebutannya adalah rg A atau r (A).

Properti peringkat matriks.

1) pangkat matriks A nxm tidak melebihi yang lebih kecil dimensinya, yaitu

r (A) ≤min (m, n).

2) r (A) \u003d 0 jika semua elemen matriks sama dengan 0, yaitu A \u003d 0.

3) Untuk matriks bujursangkar А orde ke-n r (A) \u003d n, jika А tidak berdegenerasi.

(Pangkat matriks diagonal sama dengan jumlah elemen diagonal bukan nolnya).

4) Jika rank matriks adalah r, maka matriks tersebut memiliki minimal satu minor orde r, tidak sama dengan nol, dan semua minor orde besar sama dengan nol.

Relasi berikut ini valid untuk peringkat matriks:

2) r (A + B) ≤r (A) + r (B); 3) r (AB) ≤min (r (A), r (B));

3) r (A + B) ≥│r (A) -r (B) │; 4) r (A T A) \u003d r (A);

5) r (AB) \u003d r (A) jika B adalah matriks bujursangkar non-degenerasi.

6) r (AB) ≥r (A) + r (B) -n, dimana n adalah banyaknya kolom dari matriks A atau baris matriks B.

Definisi. Sebuah minor bukan nol dari orde r (A) dipanggil dasar minor... (Matriks A dapat memiliki beberapa anak di bawah umur dasar). Baris dan kolom di persimpangan yang memiliki minor dasar diberi nama sesuai garis dasar dan kolom dasar.

Teorema 2 (tentang minor dasar).Baris dasar (kolom) tidak bergantung linier. Setiap baris (kolom apa saja) dari matriks A adalah kombinasi linier dari baris dasar (kolom).

Bukti... (Untuk string). Jika string dasar bergantung secara linier, maka menurut teorema (1) salah satu string ini akan menjadi kombinasi linier dari string dasar lainnya, maka, tanpa mengubah nilai minor dasar, seseorang dapat mengurangi kombinasi linier yang ditentukan dari string ini dan mendapatkan string nol, dan ini bertentangan. fakta bahwa base minor adalah bukan nol. Begitu garis dasar tidak bergantung secara linier.

Mari kita buktikan bahwa setiap baris dari matriks A adalah kombinasi linier dari baris-baris dasar. Karena dengan perubahan sembarang baris (kolom) determinan mempertahankan properti menjadi sama dengan nol, maka, tanpa kehilangan keumuman, kita dapat berasumsi bahwa minor dasar berada di sudut kiri atas matriks

A \u003d,itu. terletak pada r baris pertama dan r kolom pertama. Misalkan 1 £ j £ n, 1 £ i £ m. Mari kita tunjukkan bahwa determinan orde (r + 1)

Jika j £ r atau i £ r, maka determinan ini sama dengan nol, karena itu akan memiliki dua kolom identik atau dua baris identik.

Jika j\u003e r dan i\u003e r, maka determinan ini adalah minor dari orde ke-(r + 1) matriks A. peringkat matriksnya adalah r, jadi setiap minor yang berorde tinggi sama dengan 0.

Memperluasnya sesuai dengan elemen kolom terakhir (ditambahkan), kita dapatkan

a 1j A 1j + a 2j A 2j +… + a rj A rj + a ij A ij \u003d 0, di mana komplemen aljabar terakhir A ij bertepatan dengan minor dasar M r dan oleh karena itu A ij \u003d M r ≠ 0.

Membagi persamaan terakhir dengan A ij, kita dapat menyatakan elemen a ij sebagai kombinasi linier :, dimana.

Mari kita perbaiki nilai i (i\u003e r) dan dapatkan bahwa untuk setiap j (j \u003d 1,2, ..., n) elemen dari baris ke-i ei diekspresikan secara linier dalam elemen-elemen baris e 1, e 2, ..., e r, yaitu e. Garis ke-i adalah kombinasi linier dari garis alas :. Ch.d.

Teorema 3. (kondisi yang diperlukan dan cukup untuk lenyapnya determinan).Untuk determinan orde-n D menjadi nol, itu perlu dan cukup bahwa baris-barisnya (kolom) bergantung secara linier.

Bukti (h. 40). Perlu... Jika determinan orde ke-n D adalah nol, maka basis minor matriksnya berorde r

Jadi, satu garis adalah kombinasi linier dari yang lainnya. Kemudian, dengan Teorema 1, baris determinan bergantung secara linier.

Kecukupan... Jika baris-baris D bergantung secara linier, maka menurut Teorema 1 satu baris A i adalah kombinasi linier dari baris-baris yang tersisa. Dengan mengurangi kombinasi linier yang ditentukan dari garis A i tanpa mengubah nilai D, kita mendapatkan garis nol. Oleh karena itu, dengan sifat-sifat determinannya, D \u003d 0. h.t.d.

Teorema 4.Transformasi dasar tidak mengubah pangkat matriks.

Bukti... Seperti yang ditunjukkan saat mempertimbangkan properti determinan, saat mengubah matriks kuadrat, determinannya tidak berubah, atau dikalikan dengan angka bukan nol, atau tanda berubah. Dalam kasus ini, urutan tertinggi dari nol anak di bawah umur dari matriks asli dipertahankan, yaitu peringkat matriks tidak berubah. Ch.d.

Jika r (A) \u003d r (B), maka A dan B - setara: A ~ B.

Teorema 5.Dengan menggunakan transformasi elementer, matriks dapat direduksi menjadi tampilan bertahap.Matriks disebut langkah, jika berbentuk:

А \u003d, di mana a ii ≠ 0, i \u003d 1,2,…, r; r≤k.

Kondisi r≤k selalu dapat dicapai dengan transposisi.

Teorema 6.Pangkat dari matriks berundak sama dengan jumlah baris bukan nolnya .

Itu. Pangkat dari matriks berundak adalah r, karena ada minor bukan nol dari orde r:

Matriks invers, suatu algoritma untuk menghitung matriks invers.

Sistem persamaan aljabar linier, sifat dasar slough, homogenitas dan ketidakhomogenan, kesesuaian dan inkonsistensi, ketegasan slough, notasi bentuk matriks untuk slough dan solusinya

Sistem persegi, metode Cramer

Transformasi lapisan dasar. Metode Gauss untuk penelitian slough.

Kriteria kesesuaian slough, teorema Kronecker-Capelli, interpretasi geometri pada contoh 2 persamaan dengan 2 tidak diketahui.

Pengelupasan seragam. Properti solusi, fsr, teorema solusi umum untuk sistem homogen. Kriteria keberadaan solusi nontrivial.

Slough yang tidak homogen. Teorema tentang struktur larutan untuk slough yang tidak homogen. Algoritma untuk memecahkan slough yang tidak homogen.

Definisi ruang linier (vektor). Contoh lp.

Sistem vektor yang bergantung secara linier dan tidak bergantung secara linier. Kriteria ketergantungan linier.

Kondisi yang cukup untuk ketergantungan linier dan kebebasan linier sistem vektor лп. Contoh sistem bebas linier dalam ruang baris, polinomial, matriks.

Isomorfisme лп. Kriteria untuk isomorfisme ln.

Subruang лп dan lambung linier dari sistem vektor. Dimensi cangkang linier.

Teorema penyelesaian dasar

Persimpangan dan jumlah subruang, jumlah langsung subruang. Teorema tentang dimensi jumlah subruang.

Subruang solusi dari slough yang homogen, dimensi dan dasarnya. Ekspresi solusi umum dari slough homogen dalam istilah fsr.

Matriks transisi dari satu basis ke basis lainnya beserta propertinya. Transformasi koordinat vektor saat menuju ke basis lain.

Pengertian dan contoh operator linier, peta linier dan transformasi linier

Matriks operator linier, mencari koordinat gambar vektor

Tindakan dengan operator linier. Ruang linier lo

Teorema tentang isomorfisme himpunan transformasi linier ke himpunan matriks kuadrat

Matriks hasil transformasi linier. Contoh menemukan matriks operator.

Definisi dan properti dari operator invers, matriksnya.

Kriteria untuk pembalikan operator linier. Contoh operator yang dapat dibalik dan tidak dapat diubah.

Transformasi matriks dari operator linier saat meneruskan ke basis lain.

Polinomial determinan dan karakteristik dari operator linier, invariannya sehubungan dengan transformasi basis.

Kernel dan citra operator linier. Teorema penjumlahan dimensi kernel dan citra. Menemukan kernel dan jangkauan operator linier secara tetap. Peringkat dan cacat operator linier.

Teorema tentang invariansi kernel dan citra a lo a sehubungan dengan perulangan yang bepergian dengannya

Multiplisitas aljabar dan geometris dari nilai eigen dan hubungannya.

Kriteria untuk kemampuan diagonalisasi matriks operator linier, kondisi yang memadai untuk kemampuan diagonalisasi operator linier.

Teorema Hamilton-Cayley

Aljabar linier

Teori slough

Matriks, operasi dengan matriks, matriks invers. Persamaan matriks dan solusinya.

Matriks- tabel persegi panjang dari bilangan arbitrer yang disusun dalam urutan tertentu, ukuran m * n (baris demi kolom). Elemen matriks dilambangkan, di mana i adalah nomor baris dan j adalah nomor kolom.

Penambahan (pengurangan) matriks ditentukan hanya untuk matriks satu dimensi. Jumlah (selisih) matriks adalah matriks yang unsur-unsurnya merupakan penjumlahan (selisih) dari unsur-unsur matriks asal.

Perkalian (pembagian)dengan nomornya- perkalian (pembagian) setiap elemen matriks dengan nomor ini.

Perkalian matriks didefinisikan hanya untuk matriks yang jumlah kolomnya pertama sama dengan jumlah baris yang kedua.

Perkalian matriks- matriks yang elemennya diberikan oleh rumus:

Transpos matriks- seperti matriks B, baris (kolom) di antaranya adalah kolom (baris) dalam matriks A. Dilambangkan

matriks terbalik

Persamaan Matriks- persamaan bentuk A * X \u003d B adalah hasil kali matriks, jawaban persamaan ini adalah matriks X, yang ditemukan menggunakan aturan:

Ketergantungan linier dan independensi kolom (baris) dari matriks. Kriteria ketergantungan linier, kondisi yang cukup untuk ketergantungan linier dari kolom (baris) dari matriks.

Sistem baris (kolom) disebut independen linierjika kombinasi liniernya sepele (persamaan hanya berlaku untuk a1… n \u003d 0), di mana A1… n adalah kolom (baris), dan a1… n adalah koefisien muai.

Kriteria: agar sistem vektor bergantung secara linier, perlu dan cukup bahwa setidaknya satu dari vektor sistem diekspresikan secara linier dalam bentuk vektor lain dari sistem.

Kondisi yang cukup:

Determinan matriks dan propertinya

Determinan dari matriks (determinan)- angka sedemikian rupa sehingga untuk matriks persegi A dapat dihitung dari elemen-elemen matriks dengan rumus:

, di mana minor tambahan dari elemen tersebut

Properti:

Matriks invers, suatu algoritma untuk menghitung matriks invers.

matriks terbalik- matriks bujursangkar X, yang bersama-sama dengan matriks bujursangkar A dengan urutan yang sama, memenuhi ketentuan:, di mana E adalah matriks identitas dengan urutan yang sama dengan A. Setiap matriks persegi dengan determinan yang tidak sama dengan nol memiliki 1 invers. Itu ditemukan menggunakan metode transformasi dasar dan menggunakan rumus:

Konsep peringkat matriks. Teorema minor dasar. Kriteria persamaan determinan matriks. Transformasi matriks elementer. Menghitung peringkat dengan metode transformasi dasar. Perhitungan matriks invers dengan metode transformasi elementer.

Peringkat dari matriks tersebut adalahpesanan minor dasar (rg A)

Dasar minor -minor orde r tidak sama dengan nol, sehingga semua minor orde r + 1 dan lebih tinggi sama dengan nol atau tidak ada.

Teorema Minor Dasar -Dalam matriks A sembarang, setiap kolom (baris) adalah kombinasi linier dari kolom (baris) tempat basis minor berada.

Bukti:Biarkan basis minor dalam matriks m * n A ditempatkan di r baris pertama dan r kolom pertama. Pertimbangkan determinan, yang diperoleh dengan menetapkan elemen yang sesuai dari baris ke-st dan kolom ke-k ke minor dasar matriks A.

Perhatikan bahwa untuk setiap dan, determinan ini adalah nol. Jika atau, maka determinan D berisi dua baris identik atau dua kolom identik. Jika dan, maka determinan D sama dengan nol, karena merupakan minor orde (r + λ) -ro. Memperluas determinan di sepanjang baris terakhir, kita mendapatkan :, di mana pelengkap aljabar dari elemen-elemen baris terakhir. Perhatikan bahwa karena ini adalah minor basis. Oleh karena itu dimana Menuliskan persamaan terakhir untuk, kami peroleh , yaitu Kolom ke-k (untuk apa saja) adalah kombinasi linier dari kolom-kolom minor dasar, sesuai kebutuhan.

Kriteria detA \u003d 0- Determinan sama dengan nol jika dan hanya jika barisnya (kolom) bergantung secara linier.

Transformasi dasar:

1) mengalikan string dengan angka selain nol;

2) menambahkan elemen baris lain ke elemen satu baris;

3) permutasi garis;

4) menghapus salah satu baris (kolom) yang sama;

5) transposisi;

Menghitung peringkat -Ini mengikuti dari teorema minor dasar bahwa peringkat matriks A sama dengan jumlah maksimum baris bebas linier (kolom dalam matriks), maka masalah transformasi elementer adalah untuk menemukan semua baris (kolom) bebas linier.

Menghitung matriks invers- Transformasi dapat dilakukan dengan mengalikan beberapa matriks T dengan matriks A, yang merupakan hasil perkalian matriks elementer yang sesuai: TA \u003d E.

Persamaan ini berarti matriks transformasi T adalah kebalikan dari matriks tersebut. Kemudian dan, oleh karena itu,

Perhatikan bahwa baris dan kolom dari matriks dapat dilihat sebagai vektor ukuran aritmatika m dan n, masing-masing. Dengan demikian, matriks ukuran dapat diartikan sebagai kumpulan m n-dimensi atau n mvektor aritmatika -dimensi. Dengan analogi dengan vektor geometris, kami memperkenalkan konsep ketergantungan linier dan kebebasan linier baris dan kolom dari sebuah matriks.

4.8.1. Definisi. Garis
dipanggil kombinasi linier dari string dengan koefisien
jika kesetaraan benar untuk semua elemen baris ini:

,
.

4.8.2. Definisi.

String
disebut bergantung secara linierjika ada kombinasi linier nontrivial yang sama dengan baris nol, yaitu tidak semua bilangan tersebut sama dengan nol

,
.

4.8.3. Definisi.

String
disebut independen linierjika hanya kombinasi linier sepele mereka sama dengan string nol, yaitu

4.8.4. Dalil. (Kriteria untuk ketergantungan linier baris matriks)

Untuk string menjadi dependen linier, itu perlu dan cukup bahwa setidaknya satu dari mereka menjadi kombinasi linier dari yang lain.

Bukti:

Perlu. Biarkan garisnya
bergantung secara linier, maka ada kombinasi linier nontrivial dari keduanya yang sama dengan string nol:

Tanpa kehilangan keumuman, kami mengasumsikan bahwa koefisien pertama dari kombinasi linier adalah bukan nol (jika tidak baris dapat dinomori ulang). Membagi rasio ini dengan , kita mendapatkan

artinya, baris pertama adalah kombinasi linier dari yang lainnya.

Kecukupan. Biarkan salah satu baris, misalnya, , adalah kombinasi linier dari yang lainnya

yaitu, ada kombinasi string linier nontrivial
sama dengan string nol:

yang artinya garis
bergantung secara linier, sesuai kebutuhan.

Komentar.

Definisi dan pernyataan serupa dapat dirumuskan untuk kolom-kolom matriks.

§4.9. Peringkat matriks.

4.9.1. Definisi. Minor memesan matriks ukuran
disebut penentu urutan dengan elemen yang terletak di persimpangan beberapa nya garis dan kolom.

4.9.2. Definisi. Pesanan kecil bukan nol matriks ukuran
dipanggil dasar minorjika semua anak di bawah umur dari matriks pesanan
sama dengan nol.

Komentar. Matriks dapat memiliki beberapa minor dasar. Jelas, mereka semua akan berada dalam urutan yang sama. Kasus ini juga dimungkinkan ketika matriks ukuran
pesanan kecil bukan nol, dan anak di bawah umur
tidak ada, itu
.

4.9.3. Definisi. Baris (kolom) yang membentuk base minor disebut dasar baris (kolom).

4.9.4. Definisi. Berdasarkan peringkatdari sebuah matriks disebut dengan urutan minor dasarnya. Peringkat matriks dilambangkan
atau
.

Komentar.

Perhatikan bahwa karena persamaan baris dan kolom determinan, peringkat matriks tidak berubah saat dialihkan.

4.9.5. Dalil. (Varians dari peringkat matriks di bawah transformasi dasar)

Peringkat matriks tidak berubah di bawah transformasi elementernya.

Tidak ada bukti.

4.9.6. Dalil. (Tentang minor dasar).

Baris dasar (kolom) tidak bergantung linier. Setiap baris (kolom) dari matriks dapat direpresentasikan sebagai kombinasi linier dari baris dasarnya (kolom).

Bukti:

Mari kita lakukan pembuktian string. Pembuktian pernyataan untuk kolom dapat dilakukan dengan analogi.

Biarkan peringkat matriks ukuran
adalah sama , dan
- minor dasar. Tanpa kehilangan keumuman, kami berasumsi bahwa basis minor terletak di sudut kiri atas (jika tidak, Anda dapat membawa matriks ke bentuk ini menggunakan transformasi dasar):

Mari kita buktikan terlebih dahulu kemerdekaan linier dari baris dasar. Kami melakukan pembuktian dengan kontradiksi. Misalkan garis dasar bergantung secara linier. Kemudian, menurut Teorema 4.8.4, salah satu baris dapat direpresentasikan sebagai kombinasi linier dari baris dasar yang tersisa. Oleh karena itu, jika kita mengurangi kombinasi linier yang ditentukan dari string ini, maka kita mendapatkan string nol, yang berarti minor
sama dengan nol, yang bertentangan dengan definisi anak di bawah umur. Jadi, kami telah memperoleh kontradiksi; oleh karena itu, independensi linier dari baris alas terbukti.

Sekarang, mari kita buktikan bahwa setiap baris matriks dapat direpresentasikan sebagai kombinasi linier dari baris dasar. Jika jumlah baris yang dimaksud dari 1 hingga r, maka, jelas, ini dapat direpresentasikan sebagai kombinasi linier dengan koefisien yang sama dengan 1 untuk baris tersebut dan koefisien nol untuk sisa baris. Mari kita sekarang tunjukkan jika nomor baris dari
sebelum
, dapat direpresentasikan sebagai kombinasi linier dari garis dasar. Pertimbangkan matriks minor
berasal dari minor dasar
menambahkan garis dan kolom sewenang-wenang
:

Mari kita tunjukkan minor ini
dari
sebelum
dan untuk nomor kolom apa pun dari 1 hingga .

Memang kalau kolom nomor dari 1 hingga r, maka kita memiliki determinan dengan dua kolom identik, yang jelas sama dengan nol. Jika kolom nomor dari r+1 untuk dan nomor baris dari
sebelum
kemudian
adalah matriks minor dari matriks orisinal yang berurutan lebih tinggi dari minor dasar, yang artinya sama dengan nol dari definisi minor dasar. Dengan demikian, terbukti bahwa di bawah umur
adalah nol untuk nomor baris mana pun dari
sebelum
dan untuk nomor kolom apa pun dari 1 hingga ... Memperluasnya dengan kolom terakhir, kita mendapatkan:

Sini
- pelengkap aljabar yang sesuai. perhatikan itu
, karena, oleh karena itu,
adalah minor dasar. Karenanya elemen baris k dapat direpresentasikan sebagai kombinasi linier dari elemen yang sesuai dari baris dasar dengan koefisien yang tidak bergantung pada nomor kolom :

Jadi, kami telah membuktikan bahwa baris arbitrer dari matriks dapat direpresentasikan sebagai kombinasi linier dari baris dasarnya. Teorema tersebut terbukti.

Kuliah 13

4.9.7. Dalil. (Di peringkat matriks persegi non-degenerasi)

Agar matriks bujursangkar tidak berdegenerasi, pangkat matriks harus sama dengan ukuran matriks ini.

Bukti:

Perlu. Biarkan matriks persegi ukuran n adalah non-regenerasi, lalu
Oleh karena itu, determinan dari matriks tersebut adalah minor dasar, yaitu

Kecukupan. Biarlah
maka urutan minor dasar sama dengan besar kecilnya matriks, oleh karena itu minor dasar adalah determinan dari matriks tersebut , yaitu
menurut definisi anak di bawah umur dasar.

Konsekuensi.

Agar matriks persegi menjadi non-berdegenerasi, baris-barisnya harus bebas linear dan perlu dan cukup.

Bukti:

Perlu.Karena matriks bujursangkar tidak berdegenerasi, pangkatnya sama dengan ukuran matriks
artinya, determinan dari matriks tersebut adalah basis minor. Oleh karena itu, menurut Teorema 4.9.6 tentang minor dasar, baris-baris matriks tersebut bebas linear.

Kecukupan.Karena semua baris matriks tidak bergantung linier, peringkatnya tidak kurang dari ukuran matriks, dan oleh karena itu,
oleh karena itu, dengan Teorema 4.9.7 sebelumnya, matriks tidak merosot.

4.9.8. Metode membatasi anak di bawah umur untuk menemukan pangkat matriks.

Perhatikan bahwa metode ini telah dijelaskan sebagian secara implisit dalam bukti teorema minor dasar.

4.9.8.1. Definisi. Minor
dipanggil berbatasan dalam kaitannya dengan minor
jika diturunkan dari minor
menambahkan satu baris baru dan satu kolom baru dari matriks asli.

4.9.8.2. Prosedur mencari rank matriks menggunakan metode bordering minors.

Temukan matriks minor saat ini selain nol.

Kami menghitung semua anak di bawah umur yang berbatasan dengannya.

Jika semuanya sama dengan nol, maka minor saat ini adalah dasar, dan peringkat matriksnya sama dengan urutan minor saat ini.

Jika setidaknya satu bukan nol ditemukan di antara anak di bawah umur yang berbatasan, maka itu dianggap terkini dan prosedur berlanjut.

Menggunakan metode membatasi anak di bawah umur, kami menemukan peringkat matriks

Sangat mudah untuk menunjukkan minor orde dua bukan nol saat ini, misalnya,

Kami menghitung anak di bawah umur yang berbatasan dengannya:

Oleh karena itu, karena semua anak di bawah umur yang berbatasan dari urutan ketiga sama dengan nol, maka minor
adalah dasar, yaitu

Komentar. Dari contoh yang dipertimbangkan, dapat dilihat bahwa metode ini cukup melelahkan. Oleh karena itu, dalam praktiknya, metode transformasi elementer jauh lebih sering digunakan, yang akan dibahas di bawah ini.

4.9.9. Mencari rank matriks dengan metode transformasi elementer.

Berdasarkan Teorema 4.9.5, dapat dikatakan bahwa peringkat matriks tidak berubah dalam transformasi dasar (yaitu, peringkat matriks ekivalen adalah sama). Oleh karena itu, peringkat matriks sama dengan peringkat matriks berundak yang diperoleh dari yang asli dengan transformasi elementer. Pangkat dari matriks berundak jelas sama dengan jumlah baris bukan nolnya.

Kami menentukan peringkat matriks

dengan metode transformasi dasar.

Kami memberikan matriks ke tampilan bertahap:

Jumlah baris bukan nol dari matriks bertingkat yang dihasilkan adalah tiga, oleh karena itu,

4.9.10. Pangkat suatu sistem vektor dalam ruang linier.

Pertimbangkan sistem vektor
beberapa ruang linier ... Jika bergantung secara linier, maka subsistem bebas linier dapat dibedakan di dalamnya.

4.9.10.1. Definisi. Pangkat dari sistem vektor
ruang linier adalah jumlah maksimum vektor bebas linier dari sistem ini. Peringkat dari sistem vektor
dilambangkan sebagai
.

Komentar. Jika suatu sistem vektor tidak bergantung secara linier, maka pangkatnya sama dengan jumlah vektor dalam sistem.

Mari kita merumuskan teorema yang menunjukkan hubungan antara konsep pangkat sistem vektor dalam ruang linier dan pangkat matriks.

4.9.10.2. Dalil. (Di peringkat sistem vektor dalam ruang linier)

Pangkat sistem vektor dalam ruang linier sama dengan peringkat matriks yang kolom atau barisnya adalah koordinat vektor di beberapa basis ruang linier.

Tidak ada bukti.

Konsekuensi.

Agar sistem vektor dalam ruang linier menjadi bebas linier, perlu dan cukup bahwa peringkat matriks, kolom atau baris yang merupakan koordinat vektor dalam beberapa basis, sama dengan jumlah vektor sistem.

Buktinya jelas.

4.9.10.3. Teorema (Pada dimensi selubung linier).

Dimensi amplop linier vektor
ruang linier sama dengan pangkat sistem vektor ini:

Tidak ada bukti.

Misalkan k baris dan k kolom (k ≤ min (m; n)) dipilih secara sewenang-wenang dalam matriks ukuran A (m; n). Elemen-elemen matriks pada perpotongan baris dan kolom yang dipilih membentuk matriks bujursangkar berorde k, yang determinannya disebut M kk minor orde k y atau orde k ke minor dari matriks A.

Pangkat matriks adalah urutan maksimum r dari anak di bawah umur bukan nol dari matriks A, dan setiap minor yang berorde r selain nol adalah minor dasar. Penunjukan: berdering A \u003d r. Jika rang A \u003d rang B dan ukuran matriks A dan B sama, maka matriks A dan B disebut ekivalen. Penunjukan: A ~ B.

Metode utama untuk menghitung peringkat matriks adalah metode anak di bawah umur yang berbatasan dan.

Metode Perbatasan Anak di Bawah Umur

Inti dari metode anak di bawah umur yang berbatasan adalah sebagai berikut. Misalkan minor bukan nol dari orde k telah ditemukan dalam matriks. Kemudian, berikut ini, kami menganggap hanya anak di bawah umur berorde k + 1 yang mengandung (yaitu, batas) minor dari orde k, berbeda dari nol. Jika semuanya sama dengan nol, maka pangkat matriks sama dengan k, jika tidak, di antara anak-anak yang berbatasan dengan orde (k + 1), ada yang bukan nol dan seluruh prosedur diulang.

Independensi linier dari baris (kolom) dari sebuah matriks

Konsep pangkat suatu matriks berkaitan erat dengan konsep independensi linier dari baris-barisnya (kolom).

Baris matriks:

disebut dependen linier jika ada bilangan λ 1, λ 2, λ k sehingga persamaannya berlaku:

Baris matriks A disebut bebas linier jika persamaan di atas hanya dimungkinkan jika semua bilangan λ 1 \u003d λ 2 \u003d… \u003d λ k \u003d 0

Ketergantungan linier dan independensi kolom dari matriks A ditentukan dengan cara yang sama.

Jika ada baris (a l) dari matriks A (di mana (a l) \u003d (a l1, a l2, ..., a ln)) dapat direpresentasikan sebagai

Konsep kombinasi linier kolom didefinisikan dengan cara yang serupa. Teorema minor dasar berikut ini benar.

Garis dasar dan kolom alas tidak bergantung linier. Setiap baris (atau kolom) dari matriks A adalah kombinasi linier dari baris dasar (kolom), yaitu baris (kolom) yang memotong minor dasar. Dengan demikian, peringkat matriks A: peringkat A \u003d k sama dengan jumlah maksimum baris (kolom) yang independen linier dari matriks A.

Itu. pangkat matriks adalah dimensi dari matriks bujur sangkar terbesar di dalam matriks yang Anda perlukan untuk menentukan peringkat yang determinannya bukan nol. Jika matriks asli bukan persegi, atau jika berbentuk persegi, tetapi determinannya nol, maka untuk matriks kuadrat orde bawah, baris dan kolom dipilih secara sewenang-wenang.

Selain menggunakan determinan, rank suatu matriks dapat dihitung dengan jumlah baris atau kolom matriks yang bebas linear. Ini sama dengan jumlah baris atau kolom yang tidak bergantung linier, mana saja yang lebih kecil. Misalnya, jika matriks memiliki 3 baris bebas linier dan 5 kolom bebas linier, maka peringkatnya adalah tiga.

Contoh mencari rank matriks

Dengan menggunakan metode membatasi anak di bawah umur, temukan peringkat matriks

Keputusan. Kecil dari urutan kedua

m 2 minor yang berbatasan juga bukan nol. Namun, kedua anak di bawah umur dari urutan keempat berbatasan dengan M 3.

sama dengan nol. Oleh karena itu, rank matriks A adalah 3, dan minor dasar, misalnya, minor di atas M 3.

Metode transformasi elementer didasarkan pada fakta bahwa transformasi elementer dari sebuah matriks tidak mengubah rangkingnya. Dengan menggunakan transformasi ini, dimungkinkan untuk membawa matriks ke bentuk ketika semua elemennya, kecuali untuk a 11, a 22,…, a rr (r ≤min (m, n)), sama dengan nol. Ini jelas berarti bahwa berdering A \u003d r. Perhatikan bahwa jika matriks orde ke-n berbentuk matriks segitiga atas, yaitu matriks yang semua elemen di bawah diagonal utama sama dengan nol, maka definisinya sama dengan hasil kali elemen-elemen pada diagonal utama. Properti ini dapat digunakan saat menghitung peringkat matriks dengan metode transformasi elementer: Anda perlu menggunakannya untuk mereduksi matriks menjadi segitiga, dan kemudian, setelah memilih determinan yang sesuai, kami menemukan bahwa peringkat matriks sama dengan jumlah elemen bukan nol dari diagonal utama.

Dengan menggunakan metode transformasi elementer, tentukan rank matriksnya