Semuanya dimulai dengan fakta bahwa teman dari teman dari teman saya membutuhkan bantuan untuk filter ini. Melalui cara Jedi, rumor tentang ini sampai ke saya, saya berhenti berlangganan di komentar ke posting di tautan. Tampaknya telah membantu. Baiklah, saya harap.
Kisah ini membangkitkan ingatan saya tentang tahun ketiga saya, atau sesuatu, ketika saya lulus DSP sendiri, dan mengilhami saya untuk menulis artikel untuk semua orang yang tertarik dengan cara kerja filter digital, tetapi yang secara alami takut dengan formula sombong dan gambar psikedelik di (saya sudah Saya tidak berbicara tentang buku teks).
Secara umum, menurut pengalaman saya, situasi dengan buku teks dijelaskan oleh ungkapan terkenal tentang fakta bahwa Anda tidak dapat melihat hutan di balik pepohonan. Dan dengan kata lain, ketika mereka mulai menakut-nakuti Anda dengan rumus transformasi-Z dan pembagian polinomial, yang seringkali lebih panjang dari dua papan, minat pada topik mengering dengan sangat cepat. Kita akan mulai dengan yang sederhana, karena sama sekali tidak perlu melukis ekspresi kompleks yang panjang untuk memahami apa yang sedang terjadi.
Jadi, sebagai permulaan, beberapa konsep dasar sederhana.
1. Respon impuls.
Katakanlah kita memiliki kotak dengan empat pin. Kami tidak tahu apa isinya, tetapi kami tahu pasti bahwa dua pin kiri adalah pintu masuk, dan dua pin kanan adalah pintu keluar. Mari kita coba menerapkan pulsa yang sangat pendek dengan amplitudo yang sangat besar dan melihat apa yang terjadi pada keluarannya. Nah, mengapa, itu semua sama di dalam empat kutub ini - tidak jelas, karena bagaimana menjelaskannya tidak jelas, dan setidaknya kita akan melihat sesuatu.
Di sini harus dikatakan bahwa pulsa pendek (secara umum, pendek tak terhingga) dengan amplitudo besar (secara umum, tak terhingga) disebut fungsi delta dalam teori. Ngomong-ngomong, lucunya adalah bagian integral dari ini tak ada habisnya fungsinya sama dengan satu. Begitulah normalisasi.
Jadi, apa yang kita lihat pada output dari jaringan empat port dengan menerapkan fungsi delta ke input disebut respon impuls empat kutub ini. Sejauh ini, bagaimanapun, tidak jelas bagaimana ini akan membantu kita, tapi sekarang mari kita ingat hasilnya dan beralih ke konsep menarik berikutnya.
2. Konvolusi.
Singkatnya, konvolusi adalah operasi matematika yang direduksi menjadi pengintegrasian produk dari fungsi:
![]()
Ini ditunjukkan, seperti yang Anda lihat, dengan tanda bintang. Anda juga dapat melihat bahwa selama konvolusi, satu fungsi diambil dalam urutan "langsung", dan kami meneruskan "kembali ke depan" yang kedua. Tentu saja, dalam kasus diskrit, yang lebih berharga bagi umat manusia, konvolusi, seperti integral lainnya, berlanjut ke penjumlahan:

Ini akan tampak seperti abstraksi matematika yang membosankan. Namun, pada kenyataannya, konvolusi mungkin merupakan fenomena paling ajaib di dunia ini, yang mengejutkan nomor dua setelah kelahiran seseorang ke dunia, dengan satu-satunya perbedaan bahwa dari mana anak-anak itu berasal, kebanyakan orang belajar paling sedikit pada usia delapan belas tahun, sementara tentang itu, betapa berbelit-belit itu dan betapa hal itu berguna dan menakjubkan, sebagian besar penduduk bumi sama sekali tidak tahu sepanjang hidupnya.
Jadi, kekuatan dari operasi ini terletak pada fakta bahwa jika f adalah sinyal masukan sembarang, dan g adalah respons impuls dari jaringan empat port, maka hasil dari konvolusi kedua fungsi ini akan serupa dengan yang akan kita dapatkan jika kita melewatkan sinyal f melalui jaringan empat port ini.
Artinya, respons impuls adalah pemeran lengkap dari semua properti quadrupole dalam kaitannya dengan aksi input, dan konvolusi sinyal input dengannya memungkinkan Anda mengembalikan sinyal output yang sesuai. Bagi saya, ini luar biasa!
3. Filter.
Anda dapat melakukan banyak hal dengan respons impuls dan konvolusi. Misalnya, jika sinyalnya berbunyi, Anda dapat mengatur reverb, echo, chorus, flanger, dan banyak lagi; dapat dibedakan dan diintegrasikan ... Secara umum, Anda dapat membuat apa saja. Yang paling penting bagi kami sekarang adalah, tentu saja, dengan menggunakan konvolusi, filter dapat diperoleh dengan mudah.
Filter digital itu sendiri adalah konvolusi sinyal input dengan respons impuls yang sesuai dengan filter yang diinginkan.
Tetapi, tentu saja, respons impuls harus diperoleh. Kami, tentu saja, telah menemukan cara mengukurnya di atas, tetapi ada sedikit pengertian dalam tugas seperti itu - jika kami telah memasang filter, mengapa lagi kami harus mengukur sesuatu, Anda dapat menggunakannya sebagaimana adanya. Dan selain itu, nilai terpenting dari filter digital adalah bahwa mereka dapat memiliki karakteristik yang tidak dapat dicapai (atau sangat sulit dicapai) pada kenyataannya - misalnya, fase linier. Jadi tidak ada cara mengukur sama sekali, Anda hanya perlu menghitung.
4. Mendapatkan respons impuls.
Pada titik ini, di sebagian besar publikasi tentang topik tersebut, penulis mulai membuang tumpukan transformasi Z dan pecahan dari polinomial kepada pembaca, membuatnya bingung sepenuhnya. Saya tidak akan melakukan ini, saya hanya akan menjelaskan secara singkat untuk apa semua ini dan mengapa dalam praktiknya itu tidak terlalu diperlukan untuk publik yang progresif.
Misalkan kita menemukan apa yang kita inginkan dari filter dan membuat persamaan yang mendeskripsikannya. Selanjutnya, untuk mencari respons impuls, Anda dapat mengganti fungsi delta ke persamaan turunan dan mendapatkan persamaan yang diinginkan. Satu-satunya masalah adalah bagaimana melakukannya, karena fungsi delta dalam waktu tentangarea ini diatur oleh sistem yang licik, dan secara umum ada segala macam ketidakterbatasan. Jadi pada tahap ini, semuanya ternyata sangat sulit.
Di sini, itu terjadi, dan mereka ingat bahwa ada yang namanya transformasi Laplace. Dengan sendirinya, ini bukanlah satu pon kismis. Satu-satunya alasan yang ditoleransi dalam rekayasa radio justru fakta bahwa dalam ruang argumen, transisi ke mana transformasi ini, beberapa hal benar-benar menjadi lebih sederhana. Secara khusus, fungsi delta yang memberi kita begitu banyak masalah dalam domain waktu sangat mudah diungkapkan - itu hanya satu unit!
Transformasi-Z (alias transformasi Laurent) adalah versi diskrit dari transformasi Laplace.
Artinya, menerapkan transformasi Laplace (atau Z-transform, jika perlu) ke fungsi yang menjelaskan filter yang diinginkan, menggantikannya menjadi filter yang dihasilkan dan mengubahnya kembali, kita mendapatkan respons impuls. Kedengarannya mudah, siapapun bisa mencobanya. Saya tidak akan ambil risiko, karena seperti yang sudah disebutkan, transformasi Laplace itu keras, apalagi sebaliknya. Biarkan saja sebagai pilihan terakhir, dan kita sendiri akan mencari beberapa cara yang lebih sederhana untuk mendapatkan apa yang kita cari. Ada beberapa di antaranya.
Pertama, kita dapat mengingat fakta alam yang menakjubkan lainnya - karakteristik frekuensi amplitudo dan impuls dihubungkan satu sama lain melalui transformasi Fourier yang baik dan familiar. Ini berarti bahwa kita dapat menarik respons frekuensi apa pun sesuai selera kita, mengambil dari transformasi Fourier terbalik (meskipun kontinu, bahkan diskrit) dan mendapatkan respons impuls dari sistem yang mengimplementasikannya. Itu luar biasa!
Di sini, bagaimanapun, tidak akan dilakukan tanpa masalah. Pertama, tanggapan impuls yang kita dapatkan kemungkinan besar tidak terbatas (saya tidak akan menjelaskan mengapa; inilah cara dunia bekerja), jadi kita harus memotongnya di beberapa titik (dengan menetapkannya sama dengan nol di luar titik ini) dengan keputusan yang disengaja. Tetapi ini tidak akan berfungsi begitu saja - sebagai akibatnya, seperti yang Anda harapkan, akan ada distorsi dalam respons frekuensi filter yang dihitung - itu akan menjadi bergelombang, dan pemotongan frekuensi akan kabur.
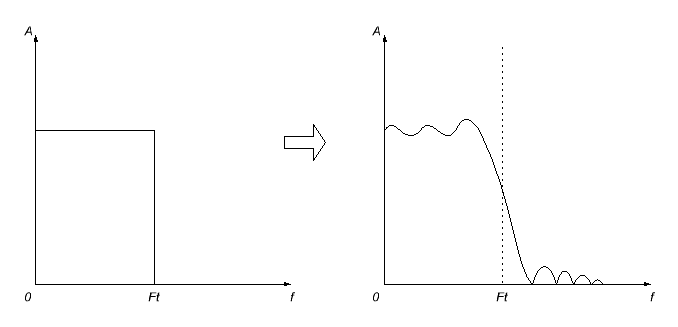
Untuk meminimalkan efek ini, berbagai fungsi perataan jendela diterapkan ke respons impuls yang dipersingkat. Akibatnya, respons frekuensi biasanya semakin kabur, tetapi osilasi yang tidak menyenangkan (terutama di jalur akses) menghilang. 
Sebenarnya, setelah pemrosesan seperti itu, kita mendapatkan respons impuls operasi dan dapat membangun filter digital.
Metode penghitungan kedua bahkan lebih sederhana - respons impuls dari filter paling populer telah lama diekspresikan dalam bentuk analitis untuk kami. Tetap hanya untuk mengganti nilai Anda dan menerapkan fungsi jendela ke hasilnya sesuai keinginan Anda. Jadi, Anda bahkan tidak perlu menghitung transformasi apa pun.
Dan, tentu saja, jika tujuannya adalah untuk meniru perilaku rangkaian tertentu, Anda bisa mendapatkan respons impulsnya di simulator:

Di sini saya menerapkan pulsa dengan tegangan 100500 volt (ya, 100,5 kV) dengan durasi 1 μs ke input rangkaian RC dan mendapatkan respons impulsnya. Jelas bahwa pada kenyataannya ini tidak dapat dilakukan, tetapi dalam simulator, metode ini, seperti yang Anda lihat, berfungsi dengan baik.
5. Catatan.
Hal tersebut di atas tentang pemendekan respons impuls, tentu saja, mengacu pada apa yang disebut. filter respons impuls hingga (filter FIR / FIR). Mereka memiliki banyak properti berharga, termasuk fase linier (dalam kondisi respons impuls tertentu), yang tidak memberikan distorsi sinyal selama penyaringan, serta stabilitas absolut. Ada juga filter dengan respons impuls tak terbatas (filter IIR / IIR). Mereka kurang intensif sumber daya dalam hal perhitungan, tetapi mereka tidak lagi memiliki keunggulan yang terdaftar.
Pada artikel berikutnya, saya berharap dapat menunjukkan kepada Anda contoh sederhana dari penerapan praktis filter digital.
Kuliah nomor 10
Filter Digital Respon Impuls Hingga
Fungsi transfer filter respons impuls hingga digital yang dapat direalisasikan secara fisik (filter FIR) dapat direpresentasikan sebagai
(10.1).
Saat mengganti dalam ekspresi (10.1), kami memperoleh respons frekuensi dari filter FIR dalam bentuk
![]() (10.2),
(10.2),
dimana ![]() - karakteristik frekuensi amplitudo (AFC) Saring,
- karakteristik frekuensi amplitudo (AFC) Saring,
![]() - karakteristik frekuensi fase (PFC) Saring.
- karakteristik frekuensi fase (PFC) Saring.
Penundaan fase Filter didefinisikan sebagai
![]() (10.3).
(10.3).
Penundaan grup Filter didefinisikan sebagai
![]() (10.4).
(10.4).
Fitur khas dari filter FIR adalah kemampuan untuk menerapkan fase konstan dan penundaan grup di dalamnya, mis. respon fase linier
(10.5),
dimana adalah sebuah konstanta. Jika kondisi ini terpenuhi, sinyal yang melewati filter tidak merusak bentuknya.
Untuk mendapatkan kondisi yang memberikan respons fase linier, kami menulis respons frekuensi filter FIR dengan mempertimbangkan (10.5)
![]() (10.6).
(10.6).
Menyamakan bagian nyata dan imajiner dari persamaan ini, kita dapatkan
 (10.7).
(10.7).
Membagi persamaan kedua dengan yang pertama, kita dapatkan
 (10.8).
(10.8).
Akhirnya, Anda bisa menulis
 (10.9).
(10.9).
Persamaan ini memiliki dua solusi. Yang pertama disebuah \u003d 0 sesuai dengan persamaan
 (10.10).
(10.10).
Persamaan ini memiliki solusi unik yang sesuai dengan sembarangh (0) (sin (0) \u003d 0), dan h (n) \u003d 0 untuk n \u003e 0. Solusi ini sesuai dengan filter yang respons impulsnya memiliki hitungan bukan nol tunggal pada waktu awal. Filter semacam itu tidak menarik secara praktis.
Mari cari solusi lain untuk. Dalam hal ini, mengalikan pembilang dan penyebut dalam (10.8), kita dapatkan
(10.11).
Oleh karena itu kami punya
![]() (10.12).
(10.12).
Karena persamaan ini berbentuk deret Fourier, solusinya, jika ada, adalah unik.
Sangat mudah untuk melihat bahwa solusi dari persamaan ini harus memenuhi persyaratan
(10.13),
(10.14).
Ini mengikuti dari kondisi (10.13) bahwa untuk setiap urutan filterN hanya ada satu penundaan fasesebuah , di mana linearitas yang ketat dari respons fase dapat dicapai. Dari kondisi (10.14) dapat disimpulkan bahwa respon impuls filter harus simetris tentang titik ganjil.N , dan relatif terhadap titik tengah interval (Gambar 10.1).
 |
Respon frekuensi dari filter semacam itu (untuk yang ganjilN ) dapat ditulis sebagai
(10.15).
Membuat substitusi dalam jumlah keduam \u003d N -1- n, kita dapatkan
(10.16).
Karena h (n) \u003d h (N -1- n ), lalu kedua jumlah tersebut dapat digabungkan
 (10.17).
(10.17).
Mengganti, kami dapatkan
(10.18).
Jika kami menunjukkan
 (10.19),
(10.19),
lalu kita akhirnya bisa menulis
 (10.20).
(10.20).
Jadi, untuk filter dengan respons fase linier, kami punya
 (10.21).
(10.21).
Untuk kasus genapN demikian pula yang akan kita miliki
 (10.22).
(10.22).
Membuat substitusi dalam jumlah kedua, kita dapatkan
 (10.23).
(10.23).
Membuat pengganti, kita dapatkan
(10.24).
Dengan menunjuk
![]() (10.25),
(10.25),
akhirnya akan memiliki
 (10.26).
(10.26).
Jadi, untuk filter FIR dengan respons fase linier dan urutan genapN bisa ditulis
 (10.27).
(10.27).
Berikut ini, untuk kesederhanaan, kami hanya akan mempertimbangkan filter dengan urutan ganjil.
Saat mensintesis fungsi transfer filter, parameter awal biasanya adalah persyaratan untuk respons frekuensi. Ada banyak teknik untuk mensintesis filter FIR. Mari kita pertimbangkan beberapa di antaranya.
Karena respons frekuensi dari setiap filter digital adalah fungsi frekuensi periodik, ini dapat direpresentasikan sebagai seri Fourier
![]() (10.28),
(10.28),
di mana koefisien deret Fourier berada
 (10.29).
(10.29).
Terlihat bahwa koefisien deret Fourierh (n ) bertepatan dengan koefisien respons impuls filter. Oleh karena itu, jika deskripsi analitis dari respons frekuensi yang diperlukan dari filter diketahui, maka dari situ dimungkinkan untuk dengan mudah menentukan koefisien respons impuls, dan darinya - fungsi transfer filter. Namun, dalam praktiknya hal ini tidak dapat dilakukan, karena respons impuls dari filter semacam itu memiliki panjang yang tak terbatas. Selain itu, filter seperti itu tidak dapat disadari secara fisik karena respons impuls dimulai pada -¥ , dan tidak ada penundaan terbatas yang akan membuat filter ini dapat diketahui secara fisik.
Salah satu metode yang mungkin untuk mendapatkan filter FIR yang mendekati respons frekuensi yang diberikan adalah memotong deret Fourier tak hingga dan respons impuls filter, dengan asumsi bahwah (n) \u003d 0 untuk. Kemudian
 (10.30).
(10.30).
Kelayakan fisik dari fungsi transferH (z ) dapat dicapai dengan mengalikanH (z) hidup.
 (10.31),
(10.31),
dimana
(10.32).
Dengan modifikasi fungsi transfer ini, karakteristik amplitudo filter tidak berubah, dan penundaan grup meningkat dengan nilai konstan.
Sebagai contoh, mari kita hitung filter FIR low-pass dengan respons frekuensi dalam bentuk
 (10.33).
(10.33).
Sesuai dengan (10.29), koefisien respons impuls filter dijelaskan oleh ekspresi
 (10.34).
(10.34).
Sekarang dari (10.31) seseorang dapat memperoleh ekspresi untuk fungsi transfer
 (10.35),
(10.35),
dimana
(10.36).
Karakteristik amplitudo dari filter yang dihitung untuk berbagaiN disajikan pada Gambar 10.2.

Gambar 10.2
Riak pada passband dan stopbands terjadi karena konvergensi yang lambat dari deret Fourier, yang, pada gilirannya, disebabkan oleh adanya diskontinuitas dalam fungsi pada frekuensi cutoff dari passband. Riak ini dikenal sebagai riak Gibbs.
Gambar 10.2 menunjukkan bahwa dengan peningkatanN frekuensi riak meningkat, dan amplitudo menurun pada frekuensi yang lebih rendah dan lebih tinggi. Namun, amplitudo riak terakhir di pita sandi dan riak pertama di pita penghenti hampir tidak berubah. Dalam prakteknya, efek seperti itu seringkali tidak diinginkan, yang membutuhkan pencarian cara untuk mengurangi denyut Gibbs.
Respon impuls terpotongh (n ) dapat direpresentasikan sebagai produk dari respons impuls tak terbatas yang diperlukan dan beberapa fungsi jendela w (n) dengan panjang n (Gambar 10.3).
![]() (10.37).
(10.37).
 |
Dalam kasus pemotongan sederhana dari deret Fourier, kami menggunakan jendela persegi panjang
 (10.38).
(10.38).
Dalam hal ini, respons frekuensi filter dapat direpresentasikan sebagai konvolusi kompleks
 (10.39).
(10.39).
Artinya, ini akan menjadi versi "buram" dari karakteristik yang diperlukan.
Masalahnya dikurangi untuk menemukan fungsi jendela yang memungkinkan untuk mengurangi denyut Gibbs dengan selektivitas filter yang sama. Untuk melakukan ini, Anda harus terlebih dahulu mempelajari properti dari fungsi jendela menggunakan contoh jendela persegi panjang.
Spektrum fungsi jendela persegi panjang dapat ditulis sebagai
 (10.40).
(10.40).
Spektrum fungsi jendela persegi panjang ditunjukkan pada Gambar 10.4.

Gambar 10.4
Karena pada, lebar lobus utama spektrum ternyata.
Kehadiran lobus samping dalam spektrum fungsi jendela menyebabkan peningkatan riak Gibbs dalam respons frekuensi filter. Untuk mendapatkan riak kecil di passband dan atenuasi besar di stopband, area yang dibatasi oleh lobus samping adalah sebagian kecil dari area yang dibatasi oleh lobus utama.
Selanjutnya, lebar lobus utama menentukan lebar zona transisi filter yang dihasilkan. Untuk selektivitas filter yang tinggi, lebar lobus utama harus sekecil mungkin. Seperti yang terlihat di atas, lebar lobus utama berkurang dengan bertambahnya urutan filter.
Dengan demikian, properti fungsi jendela yang sesuai dapat dirumuskan sebagai berikut:
- fungsi jendela harus dibatasi waktu;
- spektrum fungsi jendela sebaiknya mendekati fungsi terbatas frekuensi, yaitu. memiliki energi minimum di luar lobus utama;
- lebar lobus utama spektrum fungsi jendela harus sekecil mungkin.
Fungsi jendela yang paling umum digunakan adalah:
1. Jendela persegi panjang. Dipertimbangkan di atas.
2. Jendela Hamming.
 (10.41),
(10.41),
dimana.
Ketika jendela ini disebut jendela Henn (hanning).
3. Jendela Blackman.
 (10.42).
(10.42).
4. Jendela bartlett.
 (10.43).
(10.43).
Indikator filter yang dibuat menggunakan fungsi jendela yang ditunjukkan dirangkum dalam Tabel 10.1.
|
Jendela |
Lebar lobus utama |
Faktor riak,% |
||
N \u003d 11 |
N \u003d 21 |
N \u003d 31 |
||
|
Persegi panjang |
22.34 |
21.89 |
21.80 |
|
|
Hanning |
2.62 |
2.67 |
2.67 |
|
|
Hamming |
1.47 |
0.93 |
0.82 |
|
|
Pria kulit hitam |
0.08 |
0.12 |
0.12 |
|
Faktor riak didefinisikan sebagai rasio amplitudo lobus samping maksimum terhadap amplitudo lobus utama dalam spektrum fungsi jendela.
Untuk memilih urutan filter yang diperlukan dan fungsi jendela yang paling sesuai saat menghitung filter sebenarnya, Anda dapat menggunakan data pada Tabel 10.2.
|
transisi |
Ketidakrataan transmisi (dB) |
Atenuasi masuk hambatan (dB) |
|
|
Persegi panjang |
|||
|
Hanning |
|||
|
Hamming |
|||
|
Pria kulit hitam |
Seperti dapat dilihat dari Tabel 10.1, ada hubungan yang pasti antara faktor riak dan lebar lobus utama dalam spektrum fungsi jendela. Semakin rendah koefisien riak, semakin lebar lebar lobus utama, dan karenanya zona transisi dalam respons frekuensi filter. Untuk memastikan riak rendah pada pita akses, perlu untuk memilih jendela dengan koefisien riak yang sesuai, dan untuk menyediakan lebar zona transisi yang diperlukan dengan urutan filter N.
Masalah ini dapat diatasi dengan bantuan jendela yang disarankan oleh Kaiser. Fungsi jendela Kaiser memiliki bentuk
 (10.44),
(10.44),
dengan a adalah parameter independen, ![]() , I 0 adalah fungsi Bessel orde-nol dari jenis pertama, yang ditentukan oleh ekspresi
, I 0 adalah fungsi Bessel orde-nol dari jenis pertama, yang ditentukan oleh ekspresi
 (10.45).
(10.45).
Properti yang menarik dari jendela Kaiser adalah kemampuan untuk mengubah koefisien riak dengan mulus dari nilai kecil ke nilai besar jika hanya satu parameter a yang diubah. Dalam hal ini, untuk fungsi jendela lainnya, lebar lobus utama dapat disesuaikan dengan urutan filter N.
Parameter utama yang ditetapkan saat mengembangkan filter nyata adalah:
Bandwidth - w p;
Strip rintangan - w a;
Riak maksimum yang diijinkan pada passband - A p;
Atenuasi minimum di stopband - A a;
-frekuensi sampling -w s.
Parameter ini diilustrasikan pada Gambar 10.5. Dalam kasus ini, riak maksimum di pita sandi didefinisikan sebagai
![]() (10.46),
(10.46),
dan atenuasi minimum di stopband sebagai
Prosedur yang relatif sederhana untuk menghitung filter dengan jendela Kaiser mencakup langkah-langkah berikut:
1. Respon impuls dari filter h (n) ditentukan pada kondisi dimana respon frekuensi ideal
 (10.48),
(10.48),
dimana (10.49).
2. Parameter d dipilih sebagai
![]() (10.50),
(10.50),
dimana  (10.51).
(10.51).
3. Nilai sebenarnya dari A a dan A p dihitung dengan rumus (10.46), (10.47).
4. Pilih parameter a sebagai
 (10.52).
(10.52).
5. Pilih parameter D sebagai
 (10.53).
(10.53).
6. Nilai ganjil terkecil dari urutan filter dipilih dari kondisi
![]() (10.54),
(10.54),
 (10.57)
(10.57)
ikuti itu
Karena sampel respons impuls filter adalah koefisien dari fungsi transfernya, kondisi (10.59) berarti bahwa kode semua koefisien filter hanya berisi bagian pecahan dan bit tanda dan tidak mengandung bagian bilangan bulat.
Jumlah bit dari bagian pecahan koefisien filter ditentukan dari kondisi pemenuhan fungsi transfer filter dengan koefisien terkuantisasi, persyaratan yang ditentukan untuk perkiraan fungsi transfer referensi dengan nilai koefisien yang tepat.
Nilai absolut dari sampel sinyal input filter biasanya dinormalisasi sehingga
Jika analisis dilakukan untuk filter FIR dengan respon fasa linier, maka algoritma untuk menghitung sinyal keluarannya dapat sebagai berikut
di mana koefisien filter dibulatkan menjadi s k.
Algoritma ini sesuai dengan diagram blok dari filter yang ditunjukkan pada Gambar 10.5.
 |
Ada dua cara untuk mengimplementasikan algoritma ini. Dalam kasus pertama, semua operasi perkalian dilakukan dengan tepat dan tidak ada pembulatan hasil kali. Dalam hal ini, panjang kata produk sama dengan s in + s k, di mana s in adalah lebar sinyal input, dan s k adalah lebar koefisien filter. Dalam hal ini, diagram blok filter yang ditunjukkan pada Gambar 10.5 sama persis dengan filter yang sebenarnya.
Cara kedua dalam mengimplementasikan algoritma (10.61), setiap hasil operasi perkalian dibulatkan, yaitu. produk dihitung dengan beberapa kesalahan. Dalam hal ini, perlu untuk mengubah algoritma (10.61) untuk memperhitungkan kesalahan yang disebabkan oleh pembulatan produk
Jika nilai sampel sinyal keluaran filter dihitung sesuai dengan metode pertama (dengan nilai produk yang tepat), maka varians dari gangguan keluaran ditentukan sebagai
![]() (10.66),
(10.66),
itu. tergantung pada varians dari noise pembulatan sinyal input dan nilai koefisien filter. Dari sini Anda dapat menemukan jumlah bit yang diperlukan dari sinyal input sebagai
 (10.67).
(10.67).
Dari nilai s in dan s k yang diketahui, seseorang dapat menentukan jumlah bit yang dibutuhkan untuk bagian pecahan dari kode sinyal keluaran sebagai
Jika nilai sampel sinyal keluaran dihitung sesuai dengan metode kedua, ketika setiap produk dibulatkan menjadi s d bit, maka varians dari kebisingan pembulatan yang dihasilkan oleh masing-masing pengali dapat dinyatakan dalam lebar produk sebagai
DR masuk dan rasio signal-to-noise pada output filter SNR out. Nilai rentang dinamis dari sinyal input dalam desibel didefinisikan sebagai
![]() (10.74),
(10.74),
dengan A max dan A min adalah amplitudo maksimum dan minimum dari sinyal input filter.
Rasio signal-to-noise pada keluaran filter, dinyatakan dalam desibel, didefinisikan sebagai
![]() (10.75),
(10.75),
menentukan nilai root-mean-square dari kekuatan sinyal sinusoidal keluaran dari filter dengan amplitudo A min, dan
(10.77)
menentukan daya noise pada keluaran filter. Dari (10.75) dan (10.76) dengan A max \u003d 1 kita mendapatkan ekspresi varians dari noise output filter
![]() (10.78).
(10.78).
Nilai varians dari noise output filter ini dapat digunakan untuk menghitung lebar sinyal input dan output filter.
Mari pertimbangkan filter digital paling sederhana - filter dengan parameter konstan.
Sinyal input diumpankan ke input filter digital dalam bentuk urutan nilai numerik yang diikuti dengan interval (Gbr. 4.1, a). Ketika setiap nilai sinyal berikutnya diterima di filter digital, nilai berikutnya dari sinyal keluaran dihitung Algoritma kalkulasi bisa sangat beragam; selama kalkulasi, selain nilai terakhir dari sinyal input,
nilai sebelumnya dari sinyal input dan output: Sinyal pada output filter digital juga merupakan urutan nilai numerik, diikuti dengan interval. Interval ini sama untuk seluruh perangkat pemrosesan sinyal digital.

Angka: 4.1. Sinyal pada input dan output filter digital
Oleh karena itu, jika sinyal paling sederhana dalam bentuk pulsa tunggal diterapkan ke input filter digital (Gbr. 4.2, a)
![]()
kemudian pada output kita mendapatkan sinyal berupa urutan diskrit nilai numerik, diikuti dengan interval
Dengan analogi dengan rangkaian analog konvensional, kita menyebut sinyal respon ini respon impuls filter (Gbr. 4.2, b). Berbeda dengan respon impuls dari rangkaian analog, fungsinya tidak berdimensi.

Angka: 4.2. Impuls tunggal dan respons impuls filter digital
Mari terapkan sinyal diskrit sewenang-wenang ke masukan filter. Gambar. 4.1, a), yang merupakan sekumpulan nilai diskrit
Di bawah aksi elemen pertama, urutan dibentuk pada output filter, dikalikan dengan urutan dikalikan dan digeser ke kanan dengan nilai, dll. Sebagai hasilnya, pada output, kita mendapatkan urutan dengan

Dengan demikian, sinyal keluaran didefinisikan sebagai konvolusi diskrit dari sinyal masukan dan respons impuls. Dalam hal ini, filter digital mirip dengan rangkaian konvensional, di mana keluarannya adalah konvolusi dari masukan dan respons impuls.
Formula (4.1) adalah algoritma penyaringan digital. Jika respons impuls filter dijelaskan oleh urutan dengan jumlah anggota terbatas, maka filter dapat diimplementasikan sebagai rangkaian yang ditunjukkan pada Gambar. 4.3. Di sini huruf tersebut menunjukkan elemen penundaan sinyal untuk suatu waktu (untuk satu sel); -elemen yang mengalikan sinyal dengan faktor yang sesuai.
Sirkuit yang ditunjukkan pada Gambar. 4.3 bukan diagram pengkabelan filter digital; diagram ini adalah representasi grafis dari algoritma penyaringan digital dan menunjukkan urutan operasi aritmatika yang dilakukan selama pemrosesan sinyal.

Angka: 4.3. Sirkuit filter digital non-rekursif
Untuk filter digital yang memproses sinyal dalam bentuk urutan numerik abstrak, konsep "waktu tunda" tidak sepenuhnya benar. Oleh karena itu, elemen yang menunda sinyal dengan satu sel biasanya ditandai pada rangkaian filter digital dengan simbol yang menunjukkan penundaan sinyal dalam bahasa transformasi. Berikut ini, kami akan mematuhi sebutan ini.
Mari kembali ke rangkaian filter digital yang ditunjukkan pada Gambar. 4.3 Filter yang hanya menggunakan nilai sinyal input untuk kalkulasi disebut sederhana atau non-rekursif.
Algoritme filter non-rekursif mudah ditulis jika respons impuls filter diketahui. Untuk implementasi praktis dari algoritme, respons impuls perlu berisi sejumlah istilah yang terbatas. Jika respons impuls berisi istilah dalam jumlah tak terbatas, tetapi jumlahnya berkurang dengan cepat, maka kita dapat membatasi diri pada sejumlah istilah terbatas, membuang suku yang nilainya kecil. Jika elemen dari respon impuls tidak berkurang besarnya, algoritma filter non-rekursif ternyata tidak dapat direalisasikan.

Angka: 4.4. -rantai
Sebagai contoh, pertimbangkan filter digital paling sederhana yang mirip dengan -chain (Gbr. 4.4). Respons impuls dari -chain memiliki bentuk
![]()
Untuk menulis respons impuls dari filter digital yang sesuai, ekspresi harus diganti dengan Namun, respons impuls dari -chain tidak berdimensi dan respons impuls filter digital harus tanpa dimensi. Oleh karena itu, kami menghilangkan faktor dalam ekspresi (4.2) dan menulis respons impuls filter digital dalam bentuk
![]()
Respons impuls semacam itu mengandung banyak istilah yang tak terhingga, tetapi nilainya menurun secara eksponensial, dan Anda dapat membatasi diri pada istilah, memilih sedemikian rupa sehingga
Sekarang Anda dapat menulis ekspresi untuk sinyal pada keluaran filter
Ekspresi ini juga merupakan algoritma filter digital. Diagram filter ini ditunjukkan pada Gambar. 4.5.
Pendekatan kedua untuk analisis proses dalam filter digital mirip dengan metode operator menganalisis rangkaian analog konvensional, hanya alih-alih transformasi Laplace, -transform digunakan.

Angka: 4.5. Diagram filter digital non-rekursif yang mirip dengan -chain
Mari kita tentukan parameter filter digital, mirip dengan fungsi transfer rangkaian listrik. Untuk melakukan ini, terapkan -conversion ke respons impuls filter digital:

Fungsi tersebut disebut fungsi filter sistem.
Sesuai dengan ekspresi (4.1), sinyal pada keluaran filter digital sama dengan konvolusi diskrit dari sinyal masukan dan respons impuls filter. Menerapkan teorema konvolusi-transform pada ekspresi ini, kita mendapatkan bahwa -transformasi sinyal keluaran sama dengan -transformasi sinyal input dikalikan dengan fungsi filter sistem:
![]()
Jadi, fungsi sistem berperan sebagai fungsi transfer filter digital.
Sebagai contoh, mari kita temukan fungsi sistem dari filter digital urutan pertama yang mirip dengan -chain:

Metode ketiga untuk menganalisis perjalanan sinyal melalui filter digital mirip dengan metode klasik persamaan diferensial. Mari pertimbangkan metode ini menggunakan contoh rantai pesanan.
Rangkaian analog paling sederhana dari urutan pertama adalah rantai-a (lihat Gambar 4.4), lintasan sinyal yang dilaluinya dijelaskan oleh persamaan diferensial
![]()
Untuk rangkaian diskrit, alih-alih persamaan diferensial (4.8), persamaan perbedaan harus dituliskan, di mana sinyal input dan output ditentukan untuk momen waktu diskrit dan perbedaan nilai sinyal yang berdekatan akan muncul, bukan turunannya. Untuk rantai diskrit orde-1, persamaan perbedaan dapat dituliskan dalam bentuk yang agak umum
Kami menerapkan ke persamaan -transformation
dari mana kami menemukan fungsi filter sistem
![]()
Rumus (4.10) adalah ekspresi yang cukup umum untuk fungsi sistem filter digital urutan pertama. Ketika, ini bertepatan dengan ekspresi yang diperoleh sebelumnya (4.7) untuk fungsi sistem dari filter digital yang setara dengan -chain.
Mari kita temukan algoritma pemfilteran digital yang sesuai dengan fungsi sistem (4.10). Untuk ini, kita menyelesaikan persamaan (4.9) dengan memperhatikan
Sirkuit ekuivalen dari algoritma ini ditunjukkan pada Gambar. 4.6. Dibandingkan dengan filter non-rekursif (lihat Gambar 4.5), semacam "loop umpan balik" telah ditambahkan di sini, yang berarti bahwa nilai sinyal keluaran digunakan pada

Angka: 4.6. Skema filter digital rekursif mirip dengan -chain
perhitungan. Filter jenis ini disebut rekursif.
Algoritma (4.11) sesuai dengan filter yang sepenuhnya setara dengan filter non-rekursif yang sebelumnya dianggap. Tetapi untuk menentukan satu nilai sinyal keluaran menggunakan algoritma filter non-rekursif (4.4), diperlukan operasi, dan saat menggunakan algoritma filter rekursif (4.11), hanya diperlukan dua operasi. Ini adalah keuntungan utama dari filter rekursif. Selain itu, filter rekursif memungkinkan pemrosesan sinyal dengan presisi yang lebih tinggi, karena filter ini memungkinkan implementasi respons impuls yang lebih tepat tanpa membuang "ekor" -nya. Filter rekursif memungkinkan Anda menerapkan algoritme yang umumnya tidak mungkin dilakukan dengan filter non-rekursif. Misalnya, dengan filter yang beroperasi sesuai dengan skema pada Gambar. 4.6, pada dasarnya adalah akumulator-integrator yang ideal dan memiliki respon impuls dalam bentuk Filter dengan karakteristik seperti itu tidak dapat diimplementasikan dalam rangkaian non-rekursif.
Contoh yang dipertimbangkan menunjukkan bahwa tidak masuk akal untuk menerapkan algoritme non-rekursif untuk membuat filter digital dengan respons impuls yang panjang. Dalam kasus ini, lebih masuk akal untuk menggunakan filter rekursif.
Bidang penerapan algoritma non-rekursif adalah implementasi filter digital dengan sejumlah kecil istilah respon impuls. Contohnya adalah diferensiator sederhana yang sinyal keluarannya sama dengan kenaikan sinyal masukan:
Diagram filter digital seperti itu ditunjukkan pada Gambar. 4.7.

Angka: 4.7. Diagram pembeda digital paling sederhana
Pertimbangkan sekarang filter digital umum, yang dijelaskan oleh persamaan
Persamaan ini dapat dianggap sebagai persamaan perbedaan urutan dan sebagai algoritma penyaringan digital, jika kita menulis ulang secara berbeda, yaitu

Angka: 4.8. Sirkuit filter urutan digital rekursif
Algoritma (4.13) sesuai dengan skema yang ditunjukkan pada Gambar. 4.8. Mari kita temukan fungsi sistem dari filter semacam itu. Untuk melakukan ini, terapkan ke persamaan -transformation:
Ekspresi (4.14) memungkinkan untuk membuat sambungan antara osilasi elemen rangkaian filter dan fungsi sistem. Koefisien dalam pembilang fungsi sistem menentukan nilai koefisien pada
(di bagian non-rekursif filter), dan koefisien di penyebut menentukan bagian rekursif filter.
48 Filter digital dengan respons impuls terbatas. Perhitungan filter isyarat.
Filter Respon Impuls Hingga (Filter non-rekursif, Filter FIR) atau FIR-filter (singkatan FIR untuk respons impuls hingga) - salah satu jenis filter digital linier, fitur karakteristiknya adalah waktu respons impulsnya terbatas (dari beberapa titik waktu menjadi tepat nol). Filter semacam itu juga disebut non-rekursif karena kurangnya umpan balik. Penyebut fungsi transfer filter semacam itu adalah konstanta tertentu.
Persamaan perbedaan yang menggambarkan hubungan antara sinyal input dan output filter: dimana P.- urutan filter, x(n) - sinyal input, y(n) adalah sinyal keluaran, dan b saya - koefisien filter. Dengan kata lain, nilai dari setiap sampel sinyal keluaran ditentukan oleh jumlah nilai yang diskalakan P.sampel sebelumnya. Dapat dikatakan berbeda: nilai output filter setiap saat adalah nilai respons terhadap nilai input sesaat dan jumlah semua respons yang secara bertahap membusuk P.sampel sinyal sebelumnya yang masih mempengaruhi keluaran (setelah P.-hitung, fungsi transien impuls menjadi sama dengan nol, seperti yang telah disebutkan, oleh karena itu semua suku setelahnya P.th juga menjadi sama dengan nol). Mari tulis persamaan sebelumnya dalam bentuk yang lebih luas:

Untuk menemukan kernel filter, letakkan
x(n) = δ( n)
dimana δ ( n) adalah fungsi delta. Kemudian respons impuls dari filter FIR dapat ditulis sebagai:

Transformasi-Z dari respons impuls memberi kita fungsi transfer filter FIR:

] Properti
Filter FIR memiliki sejumlah properti berguna yang membuatnya terkadang lebih disukai untuk digunakan daripada filter IIR. Ini beberapa di antaranya:
Filter FIR kuat.
Filter FIR tidak membutuhkan umpan balik saat diterapkan.
Fase filter FIR bisa dibuat linier
Filter FIR Bentuk Langsung
Filter FIR dapat diimplementasikan menggunakan tiga elemen: multiplier, adder, dan delay unit. Varian yang ditampilkan pada gambar adalah implementasi langsung dari filter FIR Tipe 1.

Penerapan Filter FIR Formulir Langsung
Program sampel
Berikut ini adalah contoh program filter FIR yang ditulis di C:
/ * Filter FIR untuk 128 ketukan * /
float fir_filter (masukan float)
sampel float statis;
acc \u003d 0.0f; /* Baterai */
/ * Perkalian dan akumulasi * /
untuk (i \u003d 0; i< 128; i++) {
acc + \u003d (h [i] * sampel [i]);
/ * Keluaran * /
/ * Offset sinyal yang tertunda * /
untuk (i \u003d 127; i\u003e 0; i--)
sampel [i] \u003d sampel;
49 Pemulusan data. Pindah rata-rata.
50 Pemulusan data. Menghaluskan dengan parabola.
51 Pemulusan data. Menghaluskan spencer.
52 Pemulusan data. Pemfilteran median.
Bergerak rata-rata, dihaluskan oleh kelinci, penghalusan Spencer, penyaringan median
Saat mengembangkan metode untuk menentukan parameter proses fisik yang secara perlahan berubah dalam waktu, tugas penting adalah menghilangkan pengaruh efek kebisingan atau interferensi acak yang ditumpangkan pada sinyal yang diproses yang diterima pada output dari konverter utama.
Untuk menghilangkan efek ini, Anda dapat menerapkan penghalusan data. Salah satu cara termudah untuk melakukannya adalah aritmatika rata-rata. Saat diterapkan, setiap nilai fungsi diskrit (larik data yang diproses) dihitung sesuai dengan ekspresi:
dimana adalah jumlah poin untuk aritmatika averaging (integer ganjil);
Nilai fungsi berlalu sebelum diproses;
Ada juga metode penghalusan lain yang cukup efektif, misalnya, dengan parabola tingkat kedua pada lima, tujuh, sembilan, dan sebelas poin sesuai dengan ungkapan:
atau parabola tingkat empat di tujuh, sembilan, sebelas dan tiga belas poin:
Dalam aplikasi praktis, metode efektif lainnya memberikan hasil yang baik, misalnya smoothing Spencer 15 poin:
Mengganti eksponen kompleks dalam ekspresi ini, di mana, Anda dapat menentukan fungsi transfer dari transformasi terkait.
Untuk aritmatika averaging
Ekspresi dalam tanda kurung adalah perkembangan geometris dengan penyebut, oleh karena itu, ekspresi ini dapat direpresentasikan sebagai:
 .
.
Rumus ini merepresentasikan karakteristik transfer low-pass filter dan dapat dilihat bahwa semakin banyak term yang terlibat dalam rata-rata, semakin besar penekanan komponen noise frekuensi tinggi dalam sinyal (lihat Gambar 6.1).
Namun, konsep frekuensi saat memproses tren waktu berbeda dengan konsep analog saat memproses sinyal. Hal ini disebabkan oleh fakta bahwa ketika mempelajari tren waktu, yang menarik bukanlah komposisi frekuensinya, tetapi jenis perubahannya (kenaikan, penurunan, keteguhan, siklus, dll.).
Penggunaan yang disebut algoritma heuristik juga cukup efektif untuk penghalusan data.
Salah satunya adalah median filtering. Dalam pelaksanaannya dalam jendela waktu geser dimensi, di mana bilangan bulat adalah bilangan ganjil, elemen pusat digantikan oleh elemen tengah dari urutan, yang diurutkan, dalam urutan nilai menaik, elemen dari larik data dari sinyal yang dihaluskan yang termasuk dalam jendela waktu. Keuntungan dari median filtering adalah kemampuan untuk menghilangkan gangguan impuls, yang durasinya tidak melebihi, secara praktis tanpa merusak sinyal yang berubah dengan mulus. Metode peredam bising ini tidak memiliki pembenaran matematis yang ketat, tetapi kesederhanaan penghitungan dan efisiensi hasil yang diperoleh telah menyebabkan penggunaannya secara luas.

Gambar 6.1 - Grafik karakteristik transfer
operasi rata-rata aritmatika untuk m \u003d 5, 7, 9, 11
Algoritma smoothing menarik lainnya adalah rata-rata median. Esensinya adalah sebagai berikut. Dalam jendela waktu geser, dimensi (- bilangan bulat ganjil), elemen array data diurutkan dalam urutan menaik, lalu elemen pertama dan terakhir dihapus dari urutan yang diurutkan (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Metode ini memungkinkan Anda untuk menekan gangguan impuls dan frekuensi radio, serta mencapai perataan sinyal yang baik.
| " |