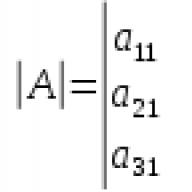მინორები და ალგებრული ავსები. როგორ გამოვთვალოთ მატრიცის განმსაზღვრელი? მცირე და ალგებრული კომპლიმენტი მეორე რიგის მატრიცის ალგებრული დანამატის გამოთვლა

განმსაზღვრელი მწკრივის ან სვეტის ელემენტებით

შემდგომი თვისებები დაკავშირებულია მცირე და ალგებრული კომპლიმენტის ცნებებთან

განმარტება. მცირეწლოვანი ელემენტს ეწოდება განმსაზღვრელი, რომელიც შედგება გადაკვეთის შემდეგ დარჩენილი ელემენტებისაგანმე-ე სანიაღვრე დაჯე სვეტი, რომლის კვეთაზე მდებარეობს ეს ელემენტი.დეტერმინანტის ელემენტის მინორი ნ- რიგითს აქვს წესრიგი ( ნ- 1). ჩვენ აღვნიშნავთ მას.

მაგალითი 1.დაე , მაშინ .

ეს მინორი მიიღება A-დან მეორე რიგისა და მესამე სვეტის გადაკვეთით.

განმარტება. ალგებრული დანამატი ელემენტს ეწოდება შესაბამისი მინორი, გამრავლებული ნატ.ე , სადმე- ხაზის ნომერი დაჯ-სვეტები, რომელთა კვეთაზე მდებარეობს ეს ელემენტი.

ვІІІ. (დეტერმინანტის დაშლა გარკვეული სტრიქონის ელემენტებად). განმსაზღვრელი უდრის გარკვეული მწკრივის ელემენტებისა და მათი შესაბამისი ალგებრული კომპლიმენტების ნამრავლების ჯამს.

.

მაგალითი 2.დაე მერე იყოს

.

მაგალითი 3.ვიპოვოთ მატრიცის განმსაზღვრელი პირველი რიგის ელემენტებში გაფართოებით.

ფორმალურად, ეს თეორემა და დეტერმინანტების სხვა თვისებები გამოიყენება მხოლოდ მესამე რიგის მატრიცების დეტერმინანტებისთვის, რადგან ჩვენ არ განვიხილავთ სხვა დეტერმინანტებს. შემდეგი განმარტება საშუალებას მოგვცემს გავაფართოვოთ ეს თვისებები ნებისმიერი რიგის დეტერმინანტებზე.

განმარტება. განმსაზღვრელი მატრიცებია n-ე რიგი არის რიცხვი, რომელიც გამოითვლება გაფართოების თეორემისა და დეტერმინანტების სხვა თვისებების თანმიმდევრული გამოყენებით..

შეგიძლიათ შეამოწმოთ, რომ გამოთვლების შედეგი არ არის დამოკიდებული ზემოაღნიშნული თვისებების გამოყენების თანმიმდევრობაზე და რომელ რიგებსა და სვეტებზე. ამ განმარტების გამოყენებით, განმსაზღვრელი ცალსახად არის ნაპოვნი.

მიუხედავად იმისა, რომ ეს განმარტება არ შეიცავს დეტერმინანტის პოვნის მკაფიო ფორმულას, ის საშუალებას აძლევს ადამიანს იპოვოთ იგი ქვედა რიგის მატრიცების დეტერმინანტებზე შემცირებით. ასეთ განმარტებებს ე.წ განმეორებადი.

მაგალითი 4.გამოთვალეთ დეტერმინანტი: .

მიუხედავად იმისა, რომ ფაქტორიზაციის თეორემა შეიძლება გამოვიყენოთ მოცემული მატრიცის ნებისმიერ მწკრივზე ან სვეტზე, ნაკლები გამოთვლები მიიღება იმ სვეტის გაყოლებით, რომელიც შეიცავს რაც შეიძლება მეტ ნულს.

ვინაიდან მატრიცას არ აქვს ნულოვანი ელემენტები, მათ ვიღებთ 7 თვისებით). გაამრავლეთ პირველი სტრიქონი თანმიმდევრულად (–5), (–3) და (–2) რიცხვებზე და დაამატეთ ის მე–2, მე–3 და მე–4 სტრიქონებს და მიიღეთ:

მოდით გავაფართოვოთ მიღებული განმსაზღვრელი პირველი სვეტის გასწვრივ და მივიღოთ:

(ვიღებთ (–4) 1-ლი სტრიქონიდან, (–2) მე-2 სტრიქონიდან, (–1) მე-3 სტრიქონიდან 4 თვისების მიხედვით)

(რადგან განმსაზღვრელი შეიცავს ორ პროპორციულ სვეტს).

§ 1.3. მატრიცების ზოგიერთი ტიპი და მათი განმსაზღვრელი

განმარტება.მოედანი მ მატრიცა ნულოვანი ელემენტებით მთავარი დიაგონალის ქვემოთ ან ზემოთ(=0 საათზე მე ჯ, ან =0 საათზე მე ჯ) დაურეკასამკუთხა .

შესაბამისად მათი სქემატური სტრუქტურა ასე გამოიყურება: ან .

აქ 0 ნიშნავს ნულ ელემენტებს და ნიშნავს თვითნებურ ელემენტებს.

თეორემა. კვადრატული სამკუთხა მატრიცის განმსაზღვრელი უდრის მთავარ დიაგონალზე მდებარე მისი ელემენტების ნამრავლს, ე.ი.

.

Მაგალითად:

.

განმარტება. კვადრატული მატრიცა ნულოვანი ელემენტებით მთავარი დიაგონალის გარეთ ეწოდებადიაგონალი .

მისი სქემატური ხედი:

დიაგონალურ მატრიცას მთავარ დიაგონალზე მხოლოდ ერთეული ელემენტებით ეწოდება მარტოხელა მატრიცა. იგი აღინიშნება:

იდენტურობის მატრიცის განმსაზღვრელი არის 1, ე.ი. E=1.

მატრიცის ტრანსფორმაციის გარეშე, განმსაზღვრელი ადვილად გამოსათვლელია მხოლოდ 2x2 და 3x3 ზომის მატრიცებისთვის. ეს კეთდება ფორმულების მიხედვით:

მატრიცისთვის

განმსაზღვრელი უდრის:

მატრიცისთვის

განმსაზღვრელი უდრის:

a11*(a22*a33-a23*a32)-a12*(a21*a33-a23*a31)+a13*(a21*a32-a22*a31)

4x4 და მეტი ზომის მატრიცების გამოთვლები რთულია, ამიტომ ისინი უნდა გარდაიქმნას დეტერმინანტის თვისებების შესაბამისად. ჩვენ უნდა ვეცადოთ მივიღოთ მატრიცა, რომელშიც ყველა მნიშვნელობა, გარდა რომელიმე სვეტისა ან მწკრივისა, ნულის ტოლია. ასეთი მატრიცის მაგალითი:

მისთვის, განმსაზღვრელი უდრის:

A12*(a21*(a33*a44-a34*a43)-a23*(a31*a44-a34*a41)+a24*(a31*a43-a33*a41))

გაითვალისწინე

a21*(a33*a44-a34*a43)-a23*(a31*a44-a34*a41)+a24*(a31*a43-a33*a41)

ეს არის მწკრივისა და სვეტის გამოკლებით მიღებული მატრიცის განმსაზღვრელი გამოთვლა, რომელთა გადაკვეთაზე არის მწკრივის/სვეტის ერთადერთი არანულოვანი რიცხვი, რომლის მიხედვითაც ვაშლით მატრიცას:

და ჩვენ ვამრავლებთ მიღებულ მნიშვნელობას იმავე რიცხვზე "ნულოვანი" სვეტიდან/სტრიქონიდან, ხოლო რიცხვი შეიძლება გავამრავლოთ -1-ზე (ყველა დეტალი ქვემოთ).

თუ მატრიცას სამკუთხა ფორმამდე შევამცირებთ, მაშინ მისი განმსაზღვრელი გამოითვლება, როგორც დიაგონალის გასწვრივ არსებული ციფრების ნამრავლი. მაგალითად, მატრიცისთვის

განმსაზღვრელი უდრის:

იგივე უნდა გაკეთდეს მატრიცებით 5x5, 6x6 და სხვა დიდი ზომები.

მატრიცული გარდაქმნები უნდა განხორციელდეს დეტერმინანტის თვისებების შესაბამისად. მაგრამ სანამ 4x4 მატრიცებისთვის დეტერმინანტის გამოთვლაზე გადავიდოდეთ, დავუბრუნდეთ 3x3 მატრიცებს და უფრო ახლოს დავაკვირდეთ, როგორ გამოითვლება მათთვის დეტერმინანტი.

მცირეწლოვანი

მატრიცის განმსაზღვრელი არც ისე ადვილი გასაგებია, რადგან მის კონცეფციაში რეკურსიაა: მატრიცის განმსაზღვრელი შედგება რამდენიმე ელემენტისგან, მათ შორის (სხვა) მატრიცების განმსაზღვრელი.

აქ ჩარჩენის თავიდან ასაცილებლად, მოდით (დროებით) ახლავე დავუშვათ, რომ მატრიცის განმსაზღვრელი არის

გამოითვლება ასე:

მოდით ასევე გავიგოთ კონვენციები და ცნებები, როგორიცაა მცირეწლოვანიდა ალგებრული დანამატი.

ასო i აღნიშნავს სტრიქონის რიგით რიცხვს, ხოლო ასო j აღნიშნავს სვეტის რიგით რიცხვს.

ij ნიშნავს მატრიცის ელემენტს (ციფრს) i მწკრივისა და j სვეტის გადაკვეთაზე.

წარმოვიდგინოთ მატრიცა, რომელიც მიიღება საწყისიდან i მწკრივის და j სვეტის ამოღებით. ახალი მატრიცის განმსაზღვრელს, რომელიც მიიღება საწყისიდან i მწკრივისა და j სვეტის ამოღებით, ეწოდება a ij ელემენტის მინორი M ij.

მოდით ილუსტრაციულად ვაჩვენოთ ნათქვამი. დავუშვათ მოცემული მატრიცა

შემდეგ, a 11 ელემენტის უმნიშვნელო M 11-ის დასადგენად, ჩვენ უნდა შევქმნათ ახალი მატრიცა, რომელიც მიიღება ორიგინალიდან პირველი მწკრივისა და პირველი სვეტის ამოღებით:

და გამოთვალეთ მისთვის განმსაზღვრელი: 2*1 – (-4)*0 = 2

a 22 ელემენტის მცირე M 22-ის დასადგენად, ჩვენ უნდა შევქმნათ ახალი მატრიცა, რომელიც მიიღება ორიგინალიდან მეორე რიგისა და მეორე სვეტის ამოღებით:

და გამოთვალეთ მისთვის განმსაზღვრელი: 1*1 -3*3 = -8

ალგებრული დანამატი

ალგებრული დანამატი A ij ელემენტისთვის a ij არის ამ ელემენტის მცირე M ij, აღებული "+" ნიშნით, თუ მწკრივისა და სვეტის ინდექსების ჯამი (i + j), რომლის გადაკვეთაზეც დგას ეს ელემენტი, არის. ლუწი და „-“ ნიშნით, თუ ინდექსების ჯამი კენტია.

ამრიგად,

წინა მაგალითის მატრიცისთვის

A 11 = (-1) (1+1) * (2*1 – (-4)*0) = 2

A 22 = (-1) (2+2) * (1*1 -3*3) = -8

მატრიცებისთვის დეტერმინანტის გამოთვლა

A მატრიცის შესაბამისი n რიგის განმსაზღვრელი არის რიცხვი, რომელიც აღინიშნება det A-ით და გამოითვლება ფორმულით:

ამ ფორმულაში ყველაფერი ჩვენთვის უკვე ნაცნობია, ახლა გამოვთვალოთ მატრიცის განმსაზღვრელი

როგორიც არ უნდა იყოს რიგის რიცხვი i = 1,2,..., n ან სვეტი j = 1, 2,..., n, n-ე რიგის განმსაზღვრელი უდრის ამ მწკრივის ელემენტების ნამრავლების ჯამს. სვეტი მათი ალგებრული დანამატებით, ე.ი.

იმათ. განმსაზღვრელი შეიძლება გამოითვალოს ნებისმიერი სვეტიდან ან ნებისმიერი მწკრივიდან.

ამის დასადასტურებლად, მოდით გამოვთვალოთ მატრიცის განმსაზღვრელი ბოლო მაგალითიდან მეორე სვეტის გამოყენებით

როგორც ხედავთ, შედეგი იდენტურია და ამ მატრიცისთვის განმსაზღვრელი ყოველთვის იქნება -52, მიუხედავად იმისა, რომელი მწკრივიდან ან სვეტიდან ვიანგარიშებთ მას.

მატრიცის დეტერმინანტის თვისებები

1. განმსაზღვრელი რიგები და სვეტები ტოლია, ანუ განმსაზღვრელი მნიშვნელობა არ შეიცვლება, თუ მისი რიგები და სვეტები შეიცვლება მათი წესრიგის შენარჩუნებისას. ამ ოპერაციას ეწოდება დეტერმინანტის ტრანსპონირება. ფორმულირებული თვისების შესაბამისად det A = det AT.
2. როდესაც ორი მწკრივი (ან ორი სვეტი) იცვლება, განმსაზღვრელი ინარჩუნებს თავის აბსოლუტურ მნიშვნელობას, მაგრამ ცვლის ნიშანს საპირისპიროდ.
3. ორი იდენტური მწკრივის (ან სვეტის) მქონე განმსაზღვრელი ნულის ტოლია.
4. დეტერმინანტის გარკვეული მწკრივის (ან რომელიმე სვეტის) ყველა ელემენტის გამრავლება λ რიცხვზე უდრის დეტერმინანტის λ რიცხვზე გამრავლებას.
5. თუ დეტერმინანტის რომელიმე მწკრივის (ან რომელიმე სვეტის) ყველა ელემენტი ნულის ტოლია, მაშინ თავად დეტერმინანტი ნულის ტოლია.
6. თუ დეტერმინანტის ორი მწკრივის (ან ორი სვეტის) ელემენტები პროპორციულია, მაშინ განმსაზღვრელი ნულის ტოლია.
7. თუ განმსაზღვრელი გარკვეული მწკრივის (ან რომელიმე სვეტის) ელემენტებს დავუმატებთ სხვა რიგის (სხვა სვეტის) შესაბამის ელემენტებს, გამრავლებულ თვითნებურ კოეფიციენტზე λ, მაშინ დეტერმინანტის მნიშვნელობა არ შეიცვლება.
8. დეტერმინანტის ნებისმიერი მწკრივის (ნებისმიერი სვეტის) ელემენტების ნამრავლების ჯამი ნებისმიერი სხვა მწკრივის (ნებისმიერი სხვა სვეტის) ელემენტების შესაბამისი ალგებრული დანამატებით ნულის ტოლია.
9. თუ დეტერმინანტის i-ე რიგის ყველა ელემენტი წარმოდგენილია ორი წევრის ჯამის სახით a ij = b j + c j, მაშინ განმსაზღვრელი უდრის ორი განმსაზღვრელთა ჯამს, რომელთა ყველა მწკრივი, გარდა i-ის, ერთნაირია. როგორც მოცემულ განმსაზღვრელში, i-ე მწკრივი ერთ-ერთ ტერმინში შედგება b j ელემენტებისაგან, ხოლო მეორეში - c j ელემენტებისაგან. მსგავსი თვისება მართალია განმსაზღვრელი სვეტებისთვის.
10. ორი კვადრატული მატრიცის ნამრავლის განმსაზღვრელი ტოლია მათი დეტერმინანტების ნამრავლის: det (A * B) = det A * det B.

ნებისმიერი რიგის დეტერმინანტის გამოსათვლელად შეგიძლიათ გამოიყენოთ განმსაზღვრელი რიგის თანმიმდევრული შემცირების მეთოდი. ამისათვის გამოიყენეთ დეტერმინანტის მწკრივის ან სვეტის ელემენტებად დაშლის წესი. დეტერმინანტების გამოთვლის კიდევ ერთი გზაა ელემენტარული გარდაქმნების გამოყენება მწკრივებით (ან სვეტებით), უპირველეს ყოვლისა, 4 და 7 დეტერმინანტების თვისებების შესაბამისად, რათა დაიყვანოთ დეტერმინანტი იმ ფორმამდე, როდესაც დეტერმინანტის მთავარ დიაგონალზეა (ასევე განსაზღვრულია. რაც შეეხება კვადრატულ მატრიცებს) ყველა ელემენტი ნულის ტოლია. მაშინ განმსაზღვრელი უდრის მთავარ დიაგონალზე მდებარე ელემენტების ნამრავლს.

დეტერმინანტის გაანგარიშებისას გამოთვლითი სამუშაოს რაოდენობის შემცირების ბრძანების თანმიმდევრული შემცირებით, მიზანშეწონილია გამოიყენოთ 7 განმსაზღვრელი თვისება, რათა მივაღწიოთ დეტერმინანტის რომელიმე მწკრივის ან სვეტის ელემენტების ნაწილის ნულიზაციას, რაც შეამცირებს რაოდენობას. გამოთვლილი ალგებრული დამატებები.

მატრიცის დაყვანა სამკუთხა ფორმამდე, მატრიცის გარდაქმნა დეტერმინანტის გამოთვლაში გასაადვილებლად

ქვემოთ ნაჩვენები მეთოდები არ არის პრაქტიკული 3x3 მატრიცებისთვის, მაგრამ მე გთავაზობთ მარტივი მაგალითის გამოყენებით შევხედოთ მეთოდების არსს. მოდით გამოვიყენოთ მატრიცა, რომლისთვისაც უკვე გამოვთვალეთ განმსაზღვრელი - გაგვიადვილდება გამოთვლების სისწორის შემოწმება:

დეტერმინანტის მე-7 თვისების გამოყენებით მეორე სტრიქონს გამოაკელი მესამე, გამრავლებული 2-ზე:

მესამე სტრიქონს გამოვაკლებთ დეტერმინანტის პირველი ხაზის შესაბამის ელემენტებს, გამრავლებული 3-ზე:

ვინაიდან მისი ძირითადი დიაგონალის ქვეშ მდებარე განმსაზღვრელი ელემენტები უდრის 0-ს, ამიტომ განსაზღვრა უდრის მთავარ დიაგონალზე მდებარე ელემენტების ნამრავლს:

1*2*(-26) = -52.

როგორც ხედავთ, პასუხი დაემთხვა ადრე მიღებულ პასუხებს.

გავიხსენოთ მატრიცის განმსაზღვრელი ფორმულა:

განმსაზღვრელი არის ალგებრული დანამატების ჯამი, გამრავლებული ერთ-ერთი მწკრივის ან ერთ-ერთი სვეტის ტერმინებზე.

თუ გარდაქმნების შედეგად ვაკეთებთ ისე, რომ ერთ-ერთი მწკრივი (ან სვეტი) მთლიანად შედგებოდეს ნულებისაგან, გარდა ერთი პოზიციისა, მაშინ არ დაგვჭირდება ყველა ალგებრული დამატებების დათვლა, რადგან ისინი აუცილებლად ნულის ტოლი იქნება. . წინა მეთოდის მსგავსად, ეს მიზანშეწონილია გამოიყენოთ დიდი მატრიცებისთვის.

მოდით აჩვენოთ მაგალითი იმავე მატრიცაზე:

ჩვენ ვამჩნევთ, რომ განმსაზღვრელი მეორე სვეტი უკვე შეიცავს ერთ ნულოვან ელემენტს. მეორე ხაზის ელემენტებს ვამატებთ პირველი ხაზის ელემენტებს, გამრავლებული -1-ზე. ჩვენ ვიღებთ:

გამოვთვალოთ განმსაზღვრელი მეორე სვეტიდან. ჩვენ უნდა გამოვთვალოთ მხოლოდ ერთი ალგებრული დამატება, რადგან დანარჩენი აშკარად ნულამდე მცირდება:

დეტერმინანტის გაანგარიშება მატრიცებისთვის 4x4, 5x5 და უფრო მაღალი ზომებისთვის

დიდი მატრიცებისთვის ძალიან ბევრი გამოთვლების თავიდან ასაცილებლად, თქვენ უნდა გააკეთოთ ზემოთ აღწერილი გარდაქმნები. მოდით მოვიყვანოთ რამდენიმე მაგალითი.

გადაწყვეტილების მატრიცების გამოთვლა

ამოხსნა.განმსაზღვრელი მე-7 თვისების გამოყენებით მეორე სტრიქონს გამოვაკლებთ მესამეს, ხოლო მეოთხე სტრიქონს განმსაზღვრელი პირველი სტრიქონის შესაბამის ელემენტებს გამრავლებული შესაბამისად 3, 4, 5. ამ მოქმედებებს შევამოკლებთ. შემდეგნაირად: (2) - (13; (3) - (1) * 4; (4) - (1) * 5. ვიღებთ:

განვახორციელოთ მოქმედებები

განმარტება.თუ n-ე რიგის განმსაზღვრელში თვითნებურად ვირჩევთ k სტრიქონებს და k სვეტებს, მაშინ ამ მწკრივებისა და სვეტების გადაკვეთაზე არსებული ელემენტები ქმნიან k რიგის კვადრატულ მატრიცას. ასეთი კვადრატული მატრიცის განმსაზღვრელი ეწოდება kth რიგის მინორი .

აღინიშნება მკ. თუ k=1, მაშინ პირველი რიგის მინორი არის დეტერმინანტის ელემენტი.

დარჩენილი (n-k) რიგებისა და (n-k) სვეტების გადაკვეთაზე არსებული ელემენტები ქმნიან რიგის კვადრატულ მატრიცას (n-k). ასეთი მატრიცის განმსაზღვრელს მინორი ეწოდება, დამატებითიარასრულწლოვან მ კ-ს. აღინიშნება Mn-k-ით.

მცირე მ კ-ის ალგებრული დანამატიჩვენ მას დავარქმევთ დამატებით მინორს, აღებული „+“ ან „-“ ნიშნით, იმისდა მიხედვით, არის თუ არა ლუწი ან კენტი ყველა მწკრივისა და სვეტის რიცხვების ჯამი, რომლებშიც მდებარეობს მცირე M k.

თუ k=1, მაშინ ელემენტის ალგებრული ავსება იკგამოითვლება ფორმულით

ა ik =(-1) i+kმ ვიცი,სადაც მ ვიცი- მცირე (n-1) შეკვეთა.

თეორემა. kth რიგის მინორისა და მისი ალგებრული დანამატის ნამრავლი უდრის D n დეტერმინანტის წევრთა გარკვეული რაოდენობის ჯამს.

მტკიცებულება

1. განვიხილოთ განსაკუთრებული შემთხვევა. მინორი M k დაიკავოს დეტერმინანტის ზედა მარცხენა კუთხეში, ანუ მდებარეობს 1, 2, ..., k ხაზებში, მაშინ უმნიშვნელო M n-k დაიკავებს k+1, k+2, ... ხაზებს. , ნ.

გამოვთვალოთ მცირე M k-ის ალგებრული დანამატი. ა-პრიორიტეტი,

ა n-k =(-1) sმ ნ-კ, სადაც s=(1+2+...+k) +(1+2+...+k)= 2(1+2+...+k), მაშინ

(-1)s=1 და ა n-k =მ ნ-კ. ვიღებთ

მ კა n-k =მ კმ ნ-კ. (*)

ვიღებთ თვითნებურ ტერმინს მცირე მ კ

სადაც s არის ჩანაცვლების ინვერსიების რაოდენობა

და თვითნებური მცირე ტერმინი მ ნ-კ

სადაც s * არის ჩანაცვლების ინვერსიების რაოდენობა

გამრავლებით (1) და (3) მივიღებთ

ნამრავლი შედგება n ელემენტისგან, რომლებიც განლაგებულია განმსაზღვრელი D-ის სხვადასხვა მწკრივებში და სვეტებში. შესაბამისად, ეს პროდუქტი არის D განმსაზღვრელი წევრი. პროდუქტის ნიშანი (5) განისაზღვრება ჩანაცვლებების (2) და ინვერსიების ჯამით. (4) და მსგავსი პროდუქტის ნიშანი D განმსაზღვრელში განისაზღვრება ინვერსიების რაოდენობა s k ჩანაცვლებაში

აშკარაა, რომ s k =s+s * .

ამრიგად, ტოლობის (*) დაბრუნებით მივიღებთ, რომ ნამრავლი M კა ნ-კშედგება მხოლოდ განმსაზღვრელი ტერმინებისგან.

2. არასრულწლოვანი მ კმდებარეობს რიგებში რიცხვებით მე 1, მე 2, ..., მე კდა სვეტებში რიცხვებით j 1, j 2, ..., j k,და მე 1< i 2 < ...< i k და j 1< j 2 < ...< j k .

დეტერმინანტების თვისებების გამოყენებით, ტრანსპოზიციების გამოყენებით ჩვენ გადავიტანთ მინორს ზედა მარცხენა კუთხეში. ჩვენ ვიღებთ დეტერმინანტს D ¢, რომელშიც მინორი M კიკავებს ზედა მარცხენა კუთხეს და დამატებით მცირე M¢ ნ-კარის ქვედა მარჯვენა კუთხე, მაშინ, იმის მიხედვით, რაც დადასტურდა 1 პუნქტში, ვიღებთ, რომ პროდუქტი M კ M¢ ნ-კარის D ¢ განმსაზღვრელი ელემენტების გარკვეული რაოდენობის ჯამი, აღებული საკუთარი ნიშნით. მაგრამ D¢ მიიღება D-დან გამოყენებით ( i 1 -1)+(i 2 -2)+ ...+(i k -k)=(i 1 + i 2 + ...+ i k)-(1+2+...+k)სიმებიანი ტრანსპოზიციები და ( j 1 -1)+(j 2 -2)+ ...+(j k -k)=(j 1 + j 2 + ...+ j k)- (1+2+...+k)სვეტის ტრანსპოზიციები. ანუ ყველაფერი გაკეთდა

(i 1 + i 2 + ...+ i k)-(1+2+...+k)+ (j 1 + j 2 + ...+ j k)- (1+2+...+k) )= (i 1 + i 2 + ...+ i k)+ (j 1 + j 2 + ...+ j k)- 2(1+2+...+k)=s-2(1+2 +...+კ).მაშასადამე, D და D ¢ დეტერმინანტების ტერმინები განსხვავდება (-1) s-2(1+2+...+k) =(-1) s ნიშნით, შესაბამისად, ნამრავლი (-1) s M. კ M¢ ნ-კშედგება D დეტერმინანტის ტერმინების გარკვეული რაოდენობისგან, აღებული იგივე ნიშნებით, რაც მათ აქვთ ამ განმსაზღვრელში.

ლაპლასის თეორემა. თუ n-ე რიგის განმსაზღვრელში ჩვენ თვითნებურად ვირჩევთ k მწკრივებს (ან k სვეტებს) 1£k£n-1, მაშინ არჩეულ მწკრივებში და მათ ალგებრულ კომპლიმენტებში შემავალი ყველა kth რიგის მცირეწლოვანთა ნამრავლების ჯამი უდრის D განმსაზღვრელს. .

მტკიცებულება

მოდით ავირჩიოთ შემთხვევითი ხაზები მე 1, მე 2, ..., მე კდა ჩვენ ამას დავამტკიცებთ

ადრე დადასტურდა, რომ ყველა ელემენტი ტოლობის მარცხენა მხარეს შეიცავს ტერმინებად D განმსაზღვრელში. მოდით ვაჩვენოთ, რომ თითოეული წევრი განმსაზღვრელი D ხვდება მხოლოდ ერთ წევრში. მართლაც, არაფერი ცროგორც ჩანს t s =. თუ ამ პროდუქტში აღვნიშნავთ იმ ფაქტორებს, რომელთა პირველი ინდექსები მე 1, მე 2, ..., მე კდა შეადგინეთ მათი პროდუქტი, მაშინ შეამჩნევთ, რომ მიღებული პროდუქტი ეკუთვნის kth რიგის მინორს. შესაბამისად, დარჩენილი ტერმინები, აღებული დარჩენილი n-k სტრიქონებიდან და n-k სვეტებიდან, ქმნიან ელემენტს, რომელიც მიეკუთვნება დამატებით მცირეს და, ნიშნის გათვალისწინებით, ალგებრულ დანამატს, შესაბამისად, ნებისმიერი. ცხვდება მხოლოდ ერთ პროდუქტში, რომელიც ადასტურებს თეორემას.

შედეგი(თეორემა ზედიზედ განმსაზღვრელი გაფართოების შესახებ) . დეტერმინანტის გარკვეული მწკრივის ელემენტებისა და შესაბამისი ალგებრული კომპლიმენტების ნამრავლების ჯამი უდრის განმსაზღვრელს.

(მტკიცებულება, როგორც სავარჯიშო.)

თეორემა. დეტერმინანტის i-ე რიგის ელემენტების ნამრავლების ჯამი j-ე რიგის ელემენტების შესაბამისი ალგებრული დანამატებით (i¹j) უდრის 0-ს.

კომენტარი. მოსახერხებელია გამოვიყენოთ ლაპლასის თეორემის დასკვნა თვისებების გამოყენებით გარდაქმნილ დეტერმინანტზე ისე, რომ ერთ მწკრივში (ან ერთ სვეტში) ყველა ელემენტი ერთის გარდა 0-ის ტოლია.

მაგალითი.გამოთვალეთ განმსაზღვრელი

12 -14 +35 -147 -20 -2= -160.

მატრიცის არასრულწლოვნები

მიეცით კვადრატი მატრიცა A, n - რიგით. მცირეწლოვანიზოგიერთ ელემენტს aij, n-ე რიგის მატრიცის განმსაზღვრელი ეწოდება განმსაზღვრელი(n - 1) - მე-ე რიგი, მიღებული ორიგინალიდან იმ მწკრივისა და სვეტის გადაკვეთით, რომელთა გადაკვეთაზე მდებარეობს შერჩეული ელემენტი aij. აღნიშნავენ მიჯ.

მოდით შევხედოთ მაგალითს მატრიცის განმსაზღვრელი 3 - მისი რიგი:
მინორები და ალგებრული კომპლიმენტები, მატრიცის 3-ის განმსაზღვრელი არის მისი რიგი, შემდეგ განმარტების მიხედვით მცირე, მცირე M12, რომელიც შეესაბამება a12 ელემენტს, იქნება განმსაზღვრელი:ამავდროულად, დახმარებით არასრულწლოვანთაშეუძლია გააადვილოს გაანგარიშების დავალება მატრიცის განმსაზღვრელი. ჩვენ უნდა გავავრცელოთ იგი მატრიცის განმსაზღვრელირაღაც ხაზით და მერე განმსაზღვრელიტოლი იქნება ამ ხაზის ყველა ელემენტის ჯამის მათი მცირერიცხოვანი. დაშლა მატრიცის განმსაზღვრელი 3 - მისი თანმიმდევრობა ასე გამოიყურება:

, პროდუქტის წინ ნიშანი არის (-1) n, სადაც n = i + j.

ალგებრული დამატებები:

ალგებრული დანამატიელემენტს aij ეწოდება მისი მცირეწლოვანი, აღებულია „+“ ნიშნით, თუ ჯამი (i + j) ლუწი რიცხვია და „-“ ნიშნით, თუ ეს ჯამი კენტი რიცხვია. აღინიშნება აიჯ.
Аij = (-1)i+j × Мij.

შემდეგ ჩვენ შეგვიძლია გადავაფორმოთ ზემოთ ჩამოთვლილი ქონება. მატრიცის განმსაზღვრელიუდრის გარკვეული მწკრივის (მწკრივის ან სვეტის) ელემენტების ნამრავლის ჯამს. მატრიცებიმათ შესაბამისს ალგებრული დამატებები. მაგალითი.

ალგებრული დანამატი- მატრიცული ალგებრის კონცეფცია; კვადრატული მატრიცის aij ელემენტთან მიმართებაში A წარმოიქმნება aij ელემენტის მინორის (1)i+j-ზე გამრავლებით; აღინიშნება Аij-ით: Aij=(1)i+jMij, სადაც Mij არის A= მატრიცის aij ელემენტის მინორი, ე.ი. განმსაზღვრელი........ ეკონომიკური და მათემატიკური ლექსიკონი

ალგებრული დანამატი- მატრიცული ალგებრის ცნება; კვადრატული მატრიცის aij ელემენტთან მიმართებაში A წარმოიქმნება aij ელემენტის მინორის (1)i+j-ზე გამრავლებით; აღინიშნება Аij-ით: Aij=(1)i+jMij, სადაც Mij არის A= მატრიცის aij ელემენტის მინორი, ე.ი. მატრიცის განმსაზღვრელი, ... ... ტექნიკური მთარგმნელის გზამკვლევი

იხილეთ ხელოვნება. განმსაზღვრელი... დიდი საბჭოთა ენციკლოპედია

მცირე M-ისთვის, რიცხვი, რომლის ტოლია, სადაც M არის k რიგის მინორი, რომელიც მდებარეობს n რიგის A კვადრატული მატრიცის მქონე რიგებში რიცხვებითა და სვეტებით; A მატრიციდან მიღებული n k რიგის მატრიცის განმსაზღვრელი მცირე M-ის მწკრივების და სვეტების წაშლით;... ... მათემატიკური ენციკლოპედია

ვიკიპედიას აქვს ჩანაწერი "დამატებით" დამატება შეიძლება ნიშნავდეს... ვიკიპედიას

ოპერაცია მოცემული X სიმრავლის ქვესიმრავლეს აყენებს სხვა ქვესიმრავლესთან შესაბამისობაში ისე, რომ თუ ცნობილია Mi N, მაშინ X სიმრავლე შეიძლება ამა თუ იმ გზით აღდგეს. იმისდა მიხედვით, თუ რა სტრუქტურით არის დაჯილდოებული X სიმრავლე,... ... მათემატიკური ენციკლოპედია

ან განმსაზღვრელი, მათემატიკაში რიცხვების ჩანაწერი კვადრატული ცხრილის სახით, რომელთანაც შესაბამისობაში მოთავსებულია სხვა რიცხვი (დეტერმინანტის მნიშვნელობა). ძალიან ხშირად, დეტერმინანტის ცნება ნიშნავს როგორც დეტერმინანტის მნიშვნელობას, ასევე მისი ჩაწერის ფორმას.…… კოლიერის ენციკლოპედია

თეორემა ალბათობის თეორიიდან იხილეთ სტატია მოივრე-ლაპლასის ლოკალური თეორემა. ლაპლასის თეორემა წრფივი ალგებრის ერთ-ერთი თეორემაა. დაარქვეს ფრანგი მათემატიკოსის პიერ სიმონ ლაპლასის (1749 1827) პატივსაცემად, რომელსაც მიეწერება ... ... ვიკიპედია

- (ლაპლასიური მატრიცა) გრაფიკის ერთ-ერთი გამოსახულება მატრიცის გამოყენებით. კირჩჰოფის მატრიცა გამოიყენება მოცემული გრაფის მოცულობითი ხეების დასათვლელად (მატრიცის ხის თეორემა) და ასევე გამოიყენება სპექტრალური გრაფიკის თეორიაში. სარჩევი 1... ...ვიკიპედია

განტოლება არის მათემატიკური ურთიერთობა, რომელიც გამოხატავს ორი ალგებრული გამონათქვამის თანასწორობას. თუ თანასწორობა ჭეშმარიტია მასში შემავალი უცნობის ნებისმიერი დასაშვები მნიშვნელობისთვის, მაშინ მას იდენტობა ეწოდება; მაგალითად, ფორმის თანაფარდობა... ... კოლიერის ენციკლოპედია

წიგნები

• დისკრეტული მათემატიკა, A.V. Chashkin. 352 გვ. სახელმძღვანელო შედგება 17 თავისგან დისკრეტული მათემატიკის ძირითად განყოფილებებზე: კომბინატორული ანალიზი, გრაფიკის თეორია, ლოგიკური ფუნქციები, გამოთვლითი სირთულე და კოდირების თეორია. შეიცავს...