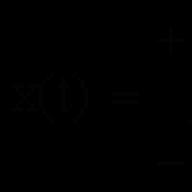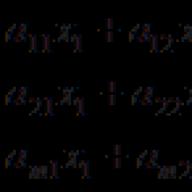unde sunt unele numere (unele sau chiar toate aceste numere pot fi zero). Aceasta înseamnă că există următoarele egalități între elementele coloanei:

sau,.

Rezultă din (3.3.1) că

(3.3.2)

unde este linia zero.

Definiție. Rândurile matricei A sunt liniar dependente dacă există numere nu toate egale cu zero în același timp

(3.3.3)

Dacă egalitatea (3.3.3) este adevărată dacă și numai dacă când, atunci rândurile sunt numite liniar independente. Relația (3.3.2) arată că, dacă unul dintre rânduri este exprimat liniar în termeni de celelalte, atunci rândurile sunt liniar dependente.

Este ușor de văzut opusul: dacă liniile sunt liniar dependente, atunci există o linie care va fi o combinație liniară a restului de linii.

Să, de exemplu, în (3.3.3), atunci .

Definiție. Să se distingă un anumit minor în matricea Ar -al ordinul și lăsați minorul (r +1) ordinea a aceleiași matrice conține în totalitate un minor. Să spunem că în acest caz minorul se învecinează cu minorul (sau este granița pentru).

Acum dovedim o lemă importantă.

Lemă despre minori limitrofi. Dacă ordinul minorr a matricei A \u003d este zero, iar toți minorii care o învecinează sunt egali cu zero, atunci orice rând (coloană) al matricei A este o combinație liniară a rândurilor (coloanelor) sale care alcătuiesc.

Dovezi. Fără a pierde generalitatea raționamentului, vom presupune că un minor diferit de zeror -ordinea a se află în colțul din stânga sus al matricei A \u003d:

Pentru primul k de rânduri ale matricei A, afirmația lemei este evidentă: este suficient să se includă același rând cu coeficientul egal cu unul în combinația liniară, iar restul - cu coeficienții egali cu zero.

Să dovedim acum că rândurile rămase ale matricei A sunt exprimate liniar în termeni de primulk linii. Pentru a face acest lucru, construiți un minor (r +1) al treilea ordin prin adăugarea minoruluilinia k () și la coloana ():

Minorul rezultat este zero pentru toțik și l ... Dacă, atunci este egal cu zero ca conținând două coloane identice. Dacă, atunci minorul rezultat este un minor mărginit pentru și, prin urmare, este egal cu zero de condiția lemmei.

Să extindem minorul prin elementele acestuia din urmăla coloană:

(3.3.4)

unde sunt complementele algebrice ale elementelor. Complementul algebric este, prin urmare, un minor al matricei A. Împărțiți (3.3.4) cu și exprimați prin:

(3.3.5)

unde,.

Presupunând că obținem:

(3.3.6)

Expresia (3.3.6) înseamnă căk -al rândul matricei A este exprimat liniar în termeni de primulr linii.

Deoarece transpunerea matricei nu modifică valorile minorilor săi (datorită proprietăților determinanților), atunci tot ceea ce a fost dovedit este valabil și pentru coloane. Teorema este dovedită.

Corolar I ... Orice rând (coloană) al unei matrice este o combinație liniară a rândurilor sale de bază (coloane). Într-adevăr, minorul de bază al matricei este diferit de zero și toți minorii care o învecinează sunt egali cu zero.

Corolar II. Determinant n - ordinul al treilea dacă și numai dacă este egal cu zero atunci când conține rânduri (coloane) liniar dependente. Suficiența dependenței liniare a rândurilor (coloanelor) pentru egalitatea determinantului la zero a fost dovedită mai devreme ca o proprietate a determinanților.

Să dovedim necesitatea. Să se dea o matrice pătratăn - ordinul al treilea, dintre care singurul minor este zero. Prin urmare, rezultă că rangul acestei matrice este mai mic decâtn , adică există cel puțin un rând care este o combinație liniară a rândurilor de bază ale acestei matrice.

Să dovedim încă o teoremă pe rangul unei matrice.

Teorema. Numărul maxim de rânduri liniar independente ale unei matrice este egal cu numărul maxim al coloanelor sale liniar independente și este egal cu rangul acestei matrice.

Dovezi. Fie rangul matricei А \u003d să fier. Apoi orice k șirurile de bază sunt liniar independente, altfel baza minoră ar fi zero. Pe de altă parte, oricer +1 sau mai multe linii sunt liniar dependente. Presupunând opusul, am putea găsi un minor de ordine mai mult decâtr diferit de zero de Corolarul 2 al lemmei anterioare. Acesta din urmă contrazice faptul că ordinea maximă a minorilor care nu sunt zero ester ... Tot ceea ce am dovedit pentru rânduri este valabil și pentru coloane.

În concluzie, prezentăm încă o metodă pentru găsirea rangului unei matrice. Rangul unei matrice poate fi determinat prin găsirea unui minor diferit de zero de ordin maxim.

La prima vedere, acest lucru necesită calcularea, deși un număr finit, dar posibil foarte mare de minori din această matrice.

Cu toate acestea, următoarea teoremă ne permite să facem simplificări semnificative în acest sens.

Teorema. Dacă minorul matricei A este diferit de zero și toți minorii care o învecinează sunt egali cu zero, atunci rangul matricei ester.

Dovezi. Este suficient să arătăm că orice subsistem de rânduri al matricei pentruS\u003e r va fi dependent liniar în condițiile teoremei (acest lucru va implica faptul că r este numărul maxim de rânduri liniar independente ale matricei sau oricare dintre minorii ei de ordin mai mare decâtk sunt egale cu zero).

Să presupunem contrariul. Lăsați rândurile să fie liniar independente. Prin lema minorilor învecinați, fiecare dintre aceștia va fi exprimată liniar în termeni de linii care conțin un minor și care, deoarece sunt diferite de zero, sunt liniar independenți:

(3.3.7)

Se consideră matricea K a coeficienților expresiilor liniare (3.3.7):

Rândurile acestei matrice sunt notate cu ... Ele vor fi liniar dependente, deoarece rangul matricei K, adică numărul maxim al liniilor sale liniar independente nu depășeșter< S ... Prin urmare, există numere, nu toate sunt egale cu zero, că

Să trecem la egalitatea componentelor

(3.3.8)

Acum ia în considerare următoarea combinație liniară:

Luați în considerare o matrice mxn arbitrară, nu neapărat pătrată.

Rangul matricei.

Conceptul de rang al unei matrice este asociat cu conceptul de dependență liniară (independență) a rândurilor (coloanelor) unei matrice. Să luăm în considerare acest concept pentru corzi. Pentru coloane - la fel.

Să denotăm chiuvetele matricei A:

e 1 \u003d (a 11, a 12, ..., a 1n); е 2 \u003d (а 21, а 22, ..., а 2n); ..., е m \u003d (а m1, а m2, ..., а mn)

e k \u003d e s dacă a kj \u003d a sj, j \u003d 1,2, ..., n

Operațiile aritmetice pe rândurile unei matrici (adunare, multiplicare cu un număr) sunt introduse ca operații efectuate element cu element: λе k \u003d (λа k1, λа k2, ..., λа kn);

e k + e s \u003d [(a k1 + a s1), (a k2 + a s2),…, (a kn + a sn)].

Linia e se numește combinație liniară liniile e 1, e 2, ..., e k, dacă este egală cu suma produselor acestor linii prin numere reale arbitrare:

е \u003d λ 1 е 1 + λ 2 е 2 + ... + λ k е k

Liniile e 1, e 2, ..., e m se numesc liniar dependent, dacă există numere reale λ 1, λ 2,…, λ m, nu toate egale cu zero, că combinația liniară a acestor rânduri este egală cu rândul zero: λ 1 е 1 + λ 2 е 2 + ... + λ m е m \u003d 0 ,Unde 0 =(0,0,…,0) (1)

Dacă combinația liniară este egală cu zero dacă și numai dacă toți coeficienții λ i sunt egali cu zero (λ 1 \u003d λ 2 \u003d… \u003d λ m \u003d 0), atunci rândurile e 1, e 2, ..., e m se numesc liniar independent.

Teorema 1... Pentru ca liniile e 1, e 2, ..., e m să fie liniar dependente, este necesar și suficient ca una dintre aceste linii să fie o combinație liniară a liniilor rămase.

Dovezi. Nevoie... Fie rândurile e 1, e 2,…, e m dependente liniar. Să, pentru claritate, în (1) λ m ≠ 0, apoi

Asa de șirul e m este o combinație liniară a restului șirurilor. Ch.d.

Adecvare... Fie una dintre linii, de exemplu e m, să fie o combinație liniară a restului de linii. Apoi, există numere astfel încât se menține egalitatea, care pot fi rescrise ca,

unde cel puțin 1 dintre coeficienți, (-1), nu este zero. Acestea. șirurile sunt liniar dependente. Ch.d.

Definiție. Minor de ordinul k a unei matrice A de dimensiunea mxn se numește un determinant al ordinului k cu elemente situate la intersecția oricărui k rând și a oricărui k coloană a matricei A. (k≤min (m, n)). ...

Exemplu., minori de ordinul 1: \u003d, \u003d;

minori de ordinul doi :, ordinul III

Matricea de ordinul 3 are 9 minori de ordinul 1, 9 minori de ordinul 2 și 1 minor de ordinul 3 (determinantul acestei matrice).

Definiție. Rangul matricei A este cea mai înaltă ordine a minorilor diferiți de zero din această matrice. Denumirea este rg A sau r (A).

Proprietăți de rang matricial.

1) rangul matricei A nxm nu depășește cea mai mică dintre dimensiunile sale, adică

r (A) ≤min (m, n).

2) r (A) \u003d 0 când toate elementele matricei sunt egale cu 0, adică A \u003d 0.

3) Pentru o matrice pătrată А de ordinul n-r (A) \u003d n, când А este nedegenerată.

(Rangul unei matrice diagonale este egal cu numărul elementelor sale diagonale diferite de zero).

4) Dacă rangul matricei este r, atunci matricea are cel puțin un minor de ordinul r, care nu este egal cu zero și toți minorii de ordine superioare sunt egali cu zero.

Următoarele relații sunt valabile pentru rândurile matricei:

2) r (A + B) ≤r (A) + r (B); 3) r (AB) ≤min (r (A), r (B));

3) r (A + B) ≥│r (A) -r (B) │; 4) r (A T A) \u003d r (A);

5) r (AB) \u003d r (A) dacă B este o matrice pătrată nedegenerată.

6) r (AB) ≥r (A) + r (B) -n, unde n este numărul de coloane ale matricei A sau rânduri ale matricei B.

Definiție. Se numește un minor nenul de ordinul r (A) bază minoră... (Matricea A poate avea mai mulți minori de bază). Rândurile și coloanele la intersecția cărora există un minor minor sunt denumite în consecință liniile de bază și coloane de bază.

Teorema 2 (asupra minorului de bază).Rândurile de bază (coloanele) sunt liniar independente. Orice rând (orice coloană) din matricea A este o combinație liniară de rânduri de bază (coloane).

Dovezi... (Pentru corzi). Dacă șirurile de bază erau liniar dependente, atunci conform teoremei (1) una dintre aceste șiruri ar fi o combinație liniară de alte șiruri de bază, atunci, fără a modifica valoarea minorului de bază, puteți scădea combinația liniară specificată din acest șir și obțineți un șir zero, iar acest lucru contrazice faptul că minorul de bază este diferit de zero. Asa de liniile de bază sunt liniar independente.

Să dovedim că orice rând al matricei A este o combinație liniară de rânduri de bază. pentru că cu modificări arbitrare de rânduri (coloane) determinantul păstrează proprietatea de a fi egal cu zero, apoi, fără pierderea generalității, putem presupune că minorul de bază se află în colțul din stânga sus al matricei

A \u003d,acestea. situat pe primele r rânduri și primele r coloane. Fie 1 £ j £ n, 1 £ i £ m. Să arătăm că determinantul ordinului (r + 1)

Dacă j £ r sau i £ r, atunci acest determinant este egal cu zero, deoarece va avea două coloane identice sau două rânduri identice.

Dacă j\u003e r și i\u003e r, atunci acest determinant este un minor de ordinul (r + 1) al matricei A. rangul matricei este r, ceea ce înseamnă că orice minor de ordin superior este egal cu 0.

Extindându-l în funcție de elementele ultimei coloane (adăugate), obținem

a 1j A 1j + a 2j A 2j + ... + a rj A rj + a ij A ij \u003d 0, unde ultimul complement algebric A ij coincide cu minorul de bază M r și deci A ij \u003d M r ≠ 0.

Împărțind ultima egalitate cu A ij, putem exprima elementul a ij ca o combinație liniară :, unde.

Să fixăm valoarea i (i\u003e r) și să obținem că pentru orice j (j \u003d 1,2, ..., n) elementele rândului i ei sunt exprimate liniar prin elementele rândurilor e 1, e 2, ..., e r, adică e. Linia a i-a este o combinație liniară de linii de bază :. Ch.d.

Teorema 3. (o condiție necesară și suficientă pentru dispariția determinantului).Pentru ca determinantul de ordinul al D-lea să fie egal cu zero, este necesar și suficient ca rândurile (coloanele) acestuia să fie liniar dependente.

Dovadă (p. 40). Nevoie... Dacă determinantul de ordinul al D-lea este zero, atunci baza minoră a matricei sale este de ordinul r

Astfel, o linie este o combinație liniară a celorlalte. Apoi, prin Teorema 1, rândurile determinantului sunt liniar dependente.

Adecvare... Dacă rândurile lui D sunt liniar dependente, atunci, conform teoremei 1, un rând A i este o combinație liniară a rândurilor rămase. Scăzând combinația liniară specificată din linia A i fără a modifica valoarea lui D, obținem linia zero. Prin urmare, prin proprietățile determinanților, D \u003d 0. h.t.d.

Teorema 4.Transformările elementare nu modifică rangul matricei.

Dovezi... Așa cum s-a arătat la luarea în considerare a proprietăților determinanților, la transformarea matricilor pătrate, determinanții lor fie nu se modifică, fie sunt înmulțiți cu un număr diferit de zero, fie semnul de schimbare. În acest caz, se păstrează cea mai înaltă ordine a minorilor diferiți de zero din matricea originală, adică rangul matricei nu se schimbă. Ch.d.

Dacă r (A) \u003d r (B), atunci A și B - echivalent: A ~ B.

Teorema 5.Folosind transformări elementare, matricea poate fi redusă la vedere în trepte.Matricea se numește pas, dacă are forma:

А \u003d, unde a ii ≠ 0, i \u003d 1,2, ..., r; r≤k.

Condiția r≤k poate fi întotdeauna atinsă prin transpunere.

Teorema 6.Rangul unei matrici în trepte este egal cu numărul rândurilor sale diferite de zero .

Acestea. Rangul matricei în trepte este r, deoarece există un minor diferit de zero de ordinul r:

Matricea inversă, un algoritm pentru calcularea matricei inverse.

Sistem de ecuații algebrice liniare, proprietăți de bază ale sloughului, omogenitate și neomogenitate, compatibilitate și inconsistență, definitivitatea sloughului, formă matricială de notație pentru slough și soluțiile sale

Sisteme pătrate, metoda lui Cramer

Transformări elementare slough. Metoda Gauss pentru cercetarea slough.

Criteriul de compatibilitate slough, teorema Kronecker-Capelli, interpretarea geometrică pe exemplul a 2 ecuații cu 2 necunoscute.

Slough omogen. Proprietatea soluției, fsr, teorema soluției generale pentru un sistem omogen. Un criteriu pentru existența unei soluții netriviale.

Slough neomogene. O teoremă asupra structurii unei soluții la un slough neomogen. Algoritm pentru rezolvarea slough neomogen.

Definiția spațiului liniar (vectorial). Exemple de lp.

Sisteme de vectori liniar dependente și liniar independente. Criteriul de dependență liniară.

Condiții suficiente pentru dependența liniară și independența liniară a sistemelor de vectori лп. Exemple de sisteme liniar independente în spațiile rândurilor, polinoamelor, matricilor.

Izomorfism лп. Un criteriu pentru izomorfismul lui ln.

Subspatiu лп și corpuri liniare ale sistemelor vectoriale. Dimensiunea unei cochilii liniare.

Teorema de completare a bazei

Intersecția și suma subspaiilor, suma directă a subspaiilor. Teorema asupra dimensiunii sumei subspatiilor.

Subspațiul soluțiilor unui slough omogen, dimensiunea și baza sa. Exprimarea soluției generale a unui slough omogen în termeni de fsr.

Matricea de tranziție de la o bază ln la alta și proprietățile sale. Transformarea coordonatelor unui vector la trecerea la o altă bază.

Definiție și exemple de operatori liniari, mapări liniare și transformări liniare

Matricea operatorului liniar, găsirea coordonatelor imaginii vectoriale

Acțiuni cu operatori liniari. Spațiu liniar lo

O teoremă a izomorfismului setului de transformări liniare la setul de matrice pătrate

Matricea produsului de transformare liniară. Exemple de găsire a matricilor operatorilor.

Definiția și proprietățile operatorului invers, matricea acestuia.

Un criteriu pentru inversibilitatea unui operator liniar. Exemple de operatori reversibili și ireversibili.

Transformarea matricei unui operator liniar la trecerea la o altă bază.

Polinomul determinant și caracteristic al unui operator liniar, invarianța lor față de transformările bazei.

Kernel și imaginea unui operator liniar. Teorema privind suma dimensiunilor nucleului și a imaginii. Găsirea nucleului și a gamei unui operator liniar într-o bază fixă. Rang și defect al unui operator liniar.

O teoremă despre invarianța nucleului și imaginea unui lo în raport cu o buclă care face naveta cu acesta

Multiplicitatea algebrică și geometrică a valorilor proprii și relația lor.

Un criteriu pentru diagonalizarea matricei unui operator liniar, condiții suficiente pentru diagonalizarea unui operator liniar.

Teorema Hamilton-Cayley

Algebră liniară

Teoria Slough

Matrici, operații cu matrici, matrice inversă. Ecuațiile matricei și soluțiile lor.

Matricea- un tabel dreptunghiular cu numere arbitrare dispuse într-o anumită ordine, dimensiunea m * n (rânduri după coloane). Elementele matricei sunt desemnate, unde i este numărul rândului și j este numărul coloanei.

Adăugare (scădere) matricile sunt definite numai pentru matricile unidimensionale. Suma (diferența) matricelor - o matrice ale cărei elemente sunt respectiv suma (diferența) elementelor matricilor originale.

Multiplicare (divizare)după număr- înmulțirea (împărțirea) fiecărui element al matricei cu acest număr.

Înmulțirea matricei este definită numai pentru matrici, numărul de coloane din prima dintre care este egal cu numărul de rânduri din a doua.

Înmulțirea matricei- o matrice ale cărei elemente sunt date de formule:

Transpunerea matricei- o astfel de matrice B, ale cărei rânduri (coloane) sunt coloanele (rândurile) din matricea originală A. Notat

matrice inversă

Ecuații matriciale- ecuațiile formei A * X \u003d B este produsul matricilor, răspunsul la această ecuație este matricea X, care se găsește folosind regulile:

Dependența liniară și independența coloanelor (rândurilor) matricei. Criteriul dependenței liniare, condiții suficiente pentru dependența liniară a coloanelor (rândurilor) matricei.

Se numește sistemul de rânduri (coloane) liniar independentdacă combinația liniară este banală (egalitatea se menține doar pentru a1 ... n \u003d 0), unde A1 ... n sunt coloane (rânduri) și aa1 ... n sunt coeficienții de expansiune.

Criteriu: pentru ca sistemul de vectori să fie dependent liniar, este necesar și suficient ca cel puțin unul dintre vectorii sistemului să fie exprimat liniar în termeni de ceilalți vectori ai sistemului.

Stare suficientă:

Determinanți matriciali și proprietățile acestora

Determinantul matricei (determinant)- un astfel de număr care pentru o matrice pătrată A poate fi calculat din elementele matricei prin formula:

, unde este minorul suplimentar al elementului

Proprietăți:

Matricea inversă, un algoritm pentru calcularea matricei inverse.

matrice inversă- o matrice pătrată X, care, împreună cu o matrice pătrată A de același ordin, îndeplinește condiția :, unde E este matricea identitară de același ordin ca A. Orice matrice pătrată cu determinant care nu este egal cu zero are 1 invers. Se găsește folosind metoda transformărilor elementare și folosind formula:

Conceptul de rang matricial. Teorema minoră de bază. Un criteriu pentru egalitatea determinantului matricei. Transformări ale matricei elementare. Calculul rangului prin metoda transformărilor elementare. Calculul matricei inverse prin metoda transformărilor elementare.

Rangul matricei estecomandă minoră de bază (rg A)

Minor de bază -un minor de ordinul r care nu este egal cu zero, astfel încât toți minorii de ordinul r + 1 și mai mare sunt egali cu zero sau nu există.

Teorema Minorului de Bază -Într-o matrice arbitrară A, fiecare coloană (rând) este o combinație liniară a coloanelor (rândurilor) în care se află minorul de bază.

Dovezi:Fie ca baza minoră din matricea m * n A să fie localizată în primele r rânduri și primele r coloane. Luați în considerare determinantul obținut prin atribuirea elementelor corespunzătoare din al doilea rând și coloana k minorei de bază a matricei A.

Rețineți că pentru orice și acest determinant este zero. Dacă sau, atunci determinantul D conține două rânduri identice sau două coloane identice. Dacă și, atunci determinantul D este egal cu zero, deoarece este un minor de ordinul (r + λ) -ro. Extinzând determinantul de-a lungul ultimei linii, obținem :, unde sunt complementele algebrice ale elementelor ultimei linii. Rețineți că, deoarece acesta este un minor minor. Prin urmare, unde Notând ultima egalitate pentru, obținem , adică Cea de-a cincea coloană (pentru orice) este o combinație liniară a coloanelor minorului de bază, după cum este necesar.

Criteriul detA \u003d 0- Determinantul este egal cu zero dacă și numai dacă rândurile (coloanele) sale sunt liniar dependente.

Transformări elementare:

1) înmulțirea unui șir cu un număr diferit de zero;

2) adăugarea elementelor unei alte linii la elementele unui rând;

3) permutarea liniilor;

4) ștergerea uneia dintre aceleași linii (coloane);

5) transpunere;

Calculul rangului -Din teorema minoră de bază rezultă că rangul matricei A este egal cu numărul maxim de rânduri liniar independente (coloane din matrice), de aceea problema transformărilor elementare este de a găsi toate rândurile liniare independente (coloane).

Calculând matricea inversă- Transformările pot fi implementate înmulțind unele matrice T cu matrice A, care este produsul matricilor elementare corespunzătoare: TA \u003d E.

Această ecuație înseamnă că matricea de transformare T este inversa matricei. Apoi și, prin urmare,

Rețineți că rândurile și coloanele matricei pot fi privite ca vectori aritmetici de dimensiuni m și n, respectiv. Astfel, matricea de dimensiuni poate fi interpretată ca o colecție m n-dimensional sau n m-vectori aritmetici dimensionali. Prin analogie cu vectorii geometrici, introducem conceptele de dependență liniară și independență liniară a rândurilor și coloanelor unei matrice.

4.8.1. Definiție. Linia
numit combinație liniară de șiruri cu coeficienți
dacă egalitatea este adevărată pentru toate elementele acestui rând:

,
.

4.8.2. Definiție.

Siruri de caractere
sunt numite liniar dependentdacă există o combinație liniară netrivială egală cu rândul zero, adică nu există toate aceste numere egale cu zero

,
.

4.8.3. Definiție.

Siruri de caractere
sunt numite liniar independentdacă numai combinația lor liniară trivială este egală cu șirul zero, adică

4.8.4. Teorema. (Criteriul pentru dependența liniară a rândurilor matriciale)

Pentru ca șirurile să fie dependente liniar, este necesar și suficient ca cel puțin una dintre ele să fie o combinație liniară a celorlalte.

Dovezi:

Nevoie. Să liniile
sunt liniar dependente, atunci există o combinație liniară netrivială a acestora egală cu șirul zero:

Fără pierderea generalității, presupunem că primul dintre coeficienții combinației liniare este diferit de zero (altfel rândurile pot fi renumerotate). Împărțind acest raport la , primim

adică prima linie este o combinație liniară a restului.

Adecvare. Să lăsăm una dintre linii, de exemplu, , este o combinație liniară a celorlalte, atunci

adică există o combinație liniară netrivială de șiruri
egal cu șirul nul:

ceea ce înseamnă liniile
sunt liniar dependente, după cum este necesar.

Cometariu.

Definiții și enunțuri similare pot fi formulate pentru coloanele unei matrice.

§4.9. Rangul matricei.

4.9.1. Definiție. Minor Ordin matrici mărimea
se numește determinant de ordine cu elemente situate la intersecția unora dintre ei linii și coloane.

4.9.2. Definiție. Comenză minoră zero matrici mărimea
numit de bază minordacă toți minorii din matricea ordinii
sunt egale cu zero.

Cometariu. O matrice poate avea mai mulți minori de bază. Evident, toate vor fi de același ordin. Cazul este posibil și atunci când matricea mărimea
ordin minor este diferit de zero, iar minorii ordinii
nu există, adică
.

4.9.3. Definiție. Se numesc rândurile (coloanele) care formează baza minoră de bază rânduri (coloane).

4.9.4. Definiție. După rangal unei matrici se numește ordinea minorului său de bază. Rangul matricei notat
sau
.

Cometariu.

Rețineți că, datorită egalității rândurilor și coloanelor determinantului, rangul matricei nu se modifică atunci când este transpusă.

4.9.5. Teorema. (Invarianța rangului matricei sub transformări elementare)

Rangul matricei nu se schimbă sub transformările sale elementare.

Nicio dovadă.

4.9.6. Teorema. (Despre minorul de bază).

Rândurile de bază (coloanele) sunt liniar independente. Orice rând (coloană) al unei matrice poate fi reprezentat ca o combinație liniară a rândurilor sale (coloane) de bază.

Dovezi:

Să efectuăm dovada pentru corzi. Dovada declarației pentru coloane poate fi efectuată prin analogie.

Fie rangul matricei dimensiuni
este egal , și
- minor minor. Fără pierderea generalității, presupunem că minorul de bază este situat în colțul din stânga sus (în caz contrar, matricea poate fi redusă la această formă folosind transformări elementare):

Să dovedim mai întâi independența liniară a rândurilor de bază. Realizăm dovada prin contradicție. Să presupunem că șirurile de bază sunt liniar dependente. Apoi, conform teoremei 4.8.4, unul dintre rânduri poate fi reprezentat ca o combinație liniară a rândurilor de bază rămase. Prin urmare, dacă scădem combinația liniară specificată din acest șir, atunci obținem un șir zero, ceea ce înseamnă că minorul
este egal cu zero, ceea ce contrazice definiția unui minor de bază. Astfel, am obținut o contradicție; prin urmare, se dovedește independența liniară a rândurilor de bază.

Să dovedim acum că orice rând al unei matrice poate fi reprezentat ca o combinație liniară de rânduri de bază. Dacă numărul liniei în cauză de la 1 la r, atunci, evident, poate fi reprezentat ca o combinație liniară cu un coeficient egal cu 1 pentru rând și coeficienți zero pentru restul liniilor. Să arătăm acum că dacă numărul liniei din
inainte de
, poate fi reprezentat ca o combinație liniară de linii de bază. Luați în considerare minorul matricei
derivat din minorul de bază
adăugând linia și o coloană arbitrară
:

Să arătăm că acest minor
din
inainte de
și pentru orice număr de coloană de la 1 la .

Într-adevăr, dacă numărul coloanei de la 1 la r, atunci avem un determinant cu două coloane identice, care este evident egal cu zero. Dacă numărul coloanei din r+1 până la și numărul liniei din
inainte de
apoi
este minorul matricei originale de ordin superior decât minorul de bază, ceea ce înseamnă că este egal cu zero din definiția minorului de bază. Astfel, se dovedește că minorul
este zero pentru orice număr de linie din
inainte de
și pentru orice număr de coloană de la 1 la ... Extinzându-l în ultima coloană, obținem:

Aici
- complementele algebrice corespunzătoare. observa asta
, deoarece, prin urmare,
este minorul de bază. De aici și elementele rândului k poate fi reprezentat ca o combinație liniară a elementelor corespunzătoare ale rândurilor de bază cu coeficienți independenți de numărul coloanei :

Astfel, am demonstrat că un rând arbitrar al unei matrice poate fi reprezentat ca o combinație liniară a rândurilor sale de bază. Teorema este dovedită.

prelegerea 13

4.9.7. Teorema. (Pe rangul unei matrice pătrate nedegenerate)

Pentru ca o matrice pătrată să nu fie degenerată, este necesar și suficient ca rangul matricei să fie egal cu dimensiunea acestei matrice.

Dovezi:

Nevoie. Fie matricea pătrată mărimea n este nedegenerat, atunci
, prin urmare, determinantul matricei este un minor de bază, adică

Adecvare. Lasa
atunci ordinea minorului de bază este egală cu dimensiunea matricei, prin urmare, minorul de bază este determinantul matricei , adică
prin definiția unui minor de bază.

Corolar.

Pentru ca o matrice pătrată să nu fie degenerată, este necesar și suficient ca rândurile sale să fie liniar independente.

Dovezi:

Nevoie.Deoarece o matrice pătrată nu este degenerată, rangul său este egal cu dimensiunea matricei
adică determinantul matricei este baza minoră. Prin urmare, prin teorema 4.9.6 pe minorul de bază, rândurile matricei sunt liniar independente.

Adecvare.Deoarece toate rândurile matricei sunt liniar independente, rangul său nu este mai mic decât dimensiunea matricei și, prin urmare,
prin urmare, prin Teorema 4.9.7 anterioară, matricea este nedegenerat.

4.9.8. Metoda de limitare a minorilor pentru găsirea rangului unei matrice.

Rețineți că această metodă a fost deja descrisă parțial implicit în dovada teoremei minore de bază.

4.9.8.1. Definiție. Minor
numit mărginind în raport cu minorul
dacă este derivat de la un minor
adăugând un rând nou și o coloană nouă din matricea originală.

4.9.8.2. Procedura pentru găsirea rangului unei matrici utilizând metoda minorilor învecinați.

Găsiți orice minor curent din matrice, altul decât zero.

Calculăm toți minorii care se învecinează cu acesta.

Dacă toate sunt egale cu zero, atunci minorul curent este de bază, iar rangul matricei este egal cu ordinea minorului curent.

Dacă cel puțin un non-zero se găsește printre minorii de la graniță, atunci este considerat actual și procedura continuă.

Folosind metoda minorilor învecinați, găsim rangul matricei

Este ușor să indicați actualul minor diferit de zero, de exemplu,

Calculăm minorii care se învecinează cu acesta:

Prin urmare, întrucât toți minorii vecini de ordinul trei sunt egali cu zero, atunci minorul
este de bază, adică

Cometariu. Se poate vedea din exemplul considerat că metoda este destul de laborioasă. Prin urmare, în practică, metoda transformărilor elementare este mult mai des utilizată, ceea ce va fi discutat mai jos.

4.9.9. Găsirea rangului unei matrice prin metoda transformărilor elementare.

Pe baza teoremei 4.9.5, se poate argumenta că rangul matricei nu se schimbă în cadrul transformărilor elementare (adică rangurile matricilor echivalente sunt egale). Prin urmare, rangul matricei este egal cu rangul matricei în trepte obținut din original prin transformări elementare. Rangul unei matrice în trepte este evident egal cu numărul rândurilor sale diferite de zero.

Definim rangul matricei

prin metoda transformărilor elementare.

Dăm matricea la o vizualizare în trepte:

Numărul de rânduri diferite de zero din matricea treptată rezultată este trei, prin urmare,

4.9.10. Rangul unui sistem de vectori într-un spațiu liniar.

Luați în considerare un sistem de vectori
ceva spațiu liniar ... Dacă este liniar dependent, atunci se poate distinge un subsistem liniar independent.

4.9.10.1. Definiție. Rangul sistemului de vectori
spațiul liniar este numărul maxim de vectori liniar independenți ai acestui sistem. Rangul sistemului de vectori
notat ca
.

Cometariu. Dacă un sistem de vectori este liniar independent, atunci rangul său este egal cu numărul de vectori din sistem.

Să formulăm o teoremă care să arate legătura dintre conceptele de rang al unui sistem de vectori într-un spațiu liniar și rangul unei matrice.

4.9.10.2. Teorema. (Pe rangul unui sistem de vectori într-un spațiu liniar)

Rangul unui sistem de vectori într-un spațiu liniar este egal cu rangul unei matrice ale cărei coloane sau rânduri sunt coordonatele vectorilor într-o bază a spațiului liniar.

Nicio dovadă.

Corolar.

Pentru ca un sistem de vectori într-un spațiu liniar să fie liniar independent, este necesar și suficient ca rangul matricei, ale cărui coloane sau rânduri să fie coordonatele vectorilor într-o anumită bază, să fie egal cu numărul de vectori ai sistemului.

Dovada este evidentă.

4.9.10.3. Teorema (Despre dimensiunea anvelopei liniare).

Dimensiunea anvelopei liniare a vectorilor
spațiul liniar este egal cu rangul acestui sistem de vectori:

Nicio dovadă.

Fie k rânduri și k coloane (k ≤ min (m; n)) alese în mod arbitrar într-o matrice A de dimensiuni (m; n). Elementele matricei de la intersecția rândurilor și coloanelor selectate formează o matrice pătrată de ordinul k, al cărei determinant se numește minor M kk de ordinul k y sau ordinul k minor al matricei A.

Rangul unei matrici este ordinul maxim r al minorilor diferiți de zero din matricea A și orice minor de ordinul r, altul decât zero, este un minor de bază. Denumire: a sunat A \u003d r. Dacă sunetul A \u003d sunetul B și dimensiunile matricilor A și B sunt aceleași, atunci matricile A și B se numesc echivalente. Denumire: A ~ B.

Principalele metode pentru calcularea rangului unei matrice sunt metoda minorilor limitrofi și.

Metoda minorilor de frontieră

Esența metodei minorilor limitrofi este următoarea. Să presupunem că un minor nenul de ordinul k a fost deja găsit în matrice. Apoi, în cele ce urmează, luăm în considerare numai acei minori de ordinul k + 1 care conțin (adică, chenar) un minor de ordinul k, diferit de zero. Dacă toate sunt egale cu zero, atunci rangul matricei este egal cu k; în caz contrar, printre minorii limitați de ordinul (k + 1), există unul diferit de zero și se repetă întreaga procedură.

Independența liniară a rândurilor (coloanelor) unei matrice

Conceptul de rang al unei matrice este strâns legat de conceptul de independență liniară a rândurilor (coloanelor) sale.

Rânduri matriciale:

sunt numiți liniar dependenți dacă există numere λ 1, λ 2, λ k astfel încât egalitatea să fie:

Rândurile matricei A sunt numite liniar independente dacă egalitatea de mai sus este posibilă numai dacă toate numerele λ 1 \u003d λ 2 \u003d ... \u003d λ k \u003d 0

Dependența liniară și independența coloanelor matricei A sunt determinate în mod similar.

Dacă orice rând (a l) al matricei A (unde (a l) \u003d (a l1, a l2, ..., a ln)) poate fi reprezentat ca

Conceptul unei combinații liniare de coloane este definit într-un mod similar. Avem următoarea teoremă minoră de bază.

Liniile de bază și coloanele de bază sunt liniar independente. Orice rând (sau coloană) al matricei A este o combinație liniară de rânduri de bază (coloane), adică rânduri (coloane) care intersectează minorul de bază. Astfel, rangul matricei A: rangul A \u003d k este egal cu numărul maxim de rânduri (coloane) liniar independente ale matricei A.

Acestea. rangul unei matrice este dimensiunea celei mai mari matrice pătrate din matricea pentru care trebuie să determinați rangul pentru care determinantul nu este zero. Dacă matricea originală nu este pătrată sau dacă este pătrată, dar determinantul ei este zero, atunci pentru matricile pătrate de ordin inferior, rândurile și coloanele sunt alese în mod arbitrar.

În afară de utilizarea determinanților, rangul unei matrici poate fi calculat prin numărul de rânduri sau coloane liniar independente ale matricei. Este egal cu numărul de rânduri sau coloane liniar independente, oricare dintre acestea este mai mic. De exemplu, dacă o matrice are 3 rânduri liniar independente și 5 coloane liniar independente, atunci rangul său este de trei.

Exemple de găsire a rangului unei matrice

Folosind metoda minorilor limitrofi, găsiți rangul matricei

Decizie. Minor de ordinul doi

minorul limitar M 2 este de asemenea diferit de zero. Cu toate acestea, ambii minori de ordinul patru se învecinează cu M 3.

sunt egale cu zero. Prin urmare, rangul matricei A este 3, iar minorul de bază este, de exemplu, minorul de mai sus M 3.

Metoda transformărilor elementare se bazează pe faptul că transformările elementare ale unei matrice nu își schimbă rangul. Folosind aceste transformări, este posibil să aducem matricea la formă atunci când toate elementele sale, cu excepția a 11, a 22, ..., a rr (r ≤min (m, n)), sunt egale cu zero. Aceasta înseamnă, evident, că a sunat A \u003d r. Rețineți că dacă matricea de ordinul n are forma unei matrice triunghiulare superioare, adică o matrice în care toate elementele de sub diagonala principală sunt egale cu zero, atunci definiția sa este egală cu produsul elementelor de pe diagonala principală. Această proprietate poate fi utilizată la calcularea rangului unei matrice prin metoda transformărilor elementare: este necesar să le folosim pentru a reduce matricea la una triunghiulară și apoi, după ce am selectat determinantul corespunzător, constatăm că rangul matricei este egal cu numărul de elemente diferite de zero din diagonala principală.

Folosind metoda transformărilor elementare, găsiți rangul matricei