Totul a început cu faptul că un prieten al unui prieten al prietenului meu avea nevoie de ajutor cu aceste filtre. Prin căile Jedi, zvonurile despre asta mi-au ajuns, m-am dezabonat în comentariile la postarea de pe link. Se pare că a ajutat. Ei bine, sper.
Această poveste a stârnit în mine amintirile celui de-al treilea an al meu, sau ceva de genul acesta, când am trecut eu însăși de DSP și m-a inspirat să scriu un articol pentru toți cei care sunt interesați de modul în care funcționează filtrele digitale, dar care sunt speriați în mod natural de formule obscene și de desene psihedelice din Nu vorbesc despre manuale).
În general, din experiența mea, situația cu manualele este descrisă de celebra frază despre faptul că nu poți vedea pădurea din spatele copacilor. Și adică, atunci când încep să te sperie de-a dreptul cu formulele de transformare Z și de diviziune polinomială, care sunt adesea mai lungi de două plăci, interesul pentru subiect se usucă extrem de repede. Vom începe cu una simplă, deoarece nu este deloc necesar să pictăm expresii complexe lungi pentru a înțelege ce se întâmplă.
Deci, pentru început, câteva concepte de bază simple.
1. Răspunsul la impuls.
Să presupunem că avem o cutie cu patru pini. Nu avem nicio idee despre ce este înăuntru, dar știm cu siguranță că cele două știfturi din stânga sunt intrarea, iar cele două știfturi din dreapta sunt ieșirea. Să încercăm să aplicăm un impuls foarte scurt de amplitudine foarte mare și să vedem ce se întâmplă la ieșire. Ei bine, de ce, este la fel că în interiorul acestui patru poli este neclar, deoarece modul de descriere este neclar, dar cel puțin vom vedea ceva.
Aici trebuie spus că un impuls scurt (în general vorbind, infinit scurt) de amplitudine mare (în general vorbind, infinit) se numește funcție delta în teorie. Apropo, lucrul amuzant este că integrala acestui lucru fără sfârşit funcția este egală cu una. Așa este normalizarea.
Deci, ceea ce am văzut la ieșirea unei rețele cu patru porturi prin aplicarea unei funcții delta la intrare se numește răspuns impuls acest patru poli. Cu toate acestea, până acum nu este clar cum ne va ajuta, dar acum să ne amintim doar de rezultat și să trecem la următorul concept interesant.
2. Convoluție.
Pe scurt, convoluția este o operație matematică care se reduce la integrarea produsului de funcții:
![]()
Este indicat, după cum puteți vedea, cu un asterisc. Puteți vedea, de asemenea, că, în timpul convoluției, o funcție este luată în ordinea „directă”, iar a doua o trecem „înapoi”. Desigur, într-un caz discret, care este mai valoros pentru umanitate, convoluția, ca orice integrantă, se transformă în însumare:

Ar părea un fel de abstractizare matematică anostă. Cu toate acestea, de fapt, pachetul este probabil cel mai magic fenomen al acestei lumi, surprinzător, al doilea după nașterea unei persoane în lume, cu singura diferență că de unde provin copiii, majoritatea oamenilor învață cel puțin până la vârsta de optsprezece ani, în timp ce despre asta, ce este o convoluție și cum este utilă și uimitoare, o mare parte din populația lumii nu are absolut nicio idee toată viața.
Deci, puterea acestei operațiuni constă în faptul că dacă f este un semnal de intrare arbitrar și g este răspunsul la impuls al unei rețele cu patru porturi, atunci rezultatul convoluției acestor două funcții va fi similar cu ceea ce am obține dacă am trece semnalul f prin această rețea cu patru porturi.
Adică, răspunsul la impuls este o distribuție completă a tuturor proprietăților cvadrupolului în raport cu acțiunea de intrare, iar convoluția semnalului de intrare cu acesta vă permite să restabiliți semnalul de ieșire corespunzător. În ceea ce mă privește, acest lucru este pur și simplu uimitor!
3. Filtre.
Puteți face multe cu răspunsul la impuls și convoluția. De exemplu, dacă semnalul este sunet, puteți organiza reverb, ecou, \u200b\u200brefren, flanger și multe altele; poate fi diferențiat și integrat ... În general, puteți crea orice. Ceea ce este cel mai important pentru noi acum este că, desigur, folosind convoluția, filtrele sunt la fel de ușor de obținut.
Filtrul digital în sine este convoluția semnalului de intrare cu un răspuns de impuls corespunzător filtrului dorit.
Dar, desigur, răspunsul la impuls trebuie obținut cumva. Desigur, ne-am gândit deja cum să-l măsurăm mai sus, dar nu are prea mult sens într-o astfel de sarcină - dacă am asamblat deja un filtru, de ce altfel ar trebui să măsurăm ceva, îl puteți folosi așa cum este. Și, în plus, cea mai importantă valoare a filtrelor digitale este că pot avea caracteristici care nu pot fi atinse (sau foarte greu de realizat) în realitate - de exemplu, o fază liniară. Deci, nu există nicio modalitate de a măsura deloc, trebuie doar să numărați.
4. Obținerea unui răspuns impuls.
În acest moment, în majoritatea publicațiilor pe această temă, autorii încep să arunce asupra cititorului munți de transformări Z și fracții din polinoame, confundându-l complet. Nu voi face acest lucru, voi explica doar pe scurt la ce servesc toate acestea și de ce în practică nu este foarte necesar pentru publicul progresist.
Să presupunem că am aflat ce vrem din filtru și am făcut o ecuație care îl descrie. Mai mult, pentru a găsi răspunsul la impuls, puteți înlocui funcția delta în ecuația derivată și obține cea dorită. Singura problemă este cum să o faceți, deoarece delta funcționează în timp desprearia este stabilită de un sistem viclean și, în general, există tot felul de infinități. Deci, în această etapă, totul se dovedește a fi teribil de dificil.
Aici se întâmplă și își amintesc că există așa ceva ca transformarea Laplace. În sine, nu este un kilogram de stafide. Singurul motiv pentru care este tolerat în ingineria radio este tocmai faptul că, în spațiul argumentului, la care această transformare este o tranziție, unele lucruri devin într-adevăr mai simple. În special, chiar funcția delta care ne-a dat atâtea probleme în domeniul timpului este foarte ușor de exprimat - acolo este doar o unitate!
Transformata Z (aka transformata Laurent) este o versiune discretă a transformatei Laplace.
Adică, aplicând transformata Laplace (sau transformata Z, dacă este necesar) la funcția care descrie filtrul dorit, înlocuind unitatea în cea rezultată și transformând-o înapoi, obținem un răspuns de impuls. Sună ușor, oricine îl poate încerca. Nu o să risc, pentru că, așa cum am menționat deja, transformata Laplace este un lucru dur, mai ales opusul. Să-l lăsăm ca o ultimă soluție și noi înșine vom căuta câteva modalități mai simple de a obține ceea ce căutăm. Există mai multe dintre ele.
În primul rând, ne putem aminti un alt fapt uimitor al naturii - amplitudinea-frecvență și caracteristicile impulsului sunt legate între ele prin transformarea Fourier amabilă și familiară. Aceasta înseamnă că putem atrage orice răspuns de frecvență după gustul nostru, putem prelua transformata Fourier inversă (deși continuă, chiar discretă) și să obținem răspunsul la impuls al sistemului care o implementează. Este minunat!
Aici, însă, nu se va descurca fără probleme. În primul rând, răspunsul la impuls pe care îl obținem va fi probabil infinit (nu voi intra în a explica de ce; așa funcționează lumea), așa că va trebui să îl întrerupem la un moment dat (stabilindu-l egal la zero dincolo de acest punct) printr-o decizie intenționată. Dar nu va funcționa exact așa - ca urmare, așa cum v-ați aștepta, vor exista distorsiuni ale răspunsului în frecvență al filtrului calculat - va deveni ondulat, iar tăierea de frecvență se va estompa.
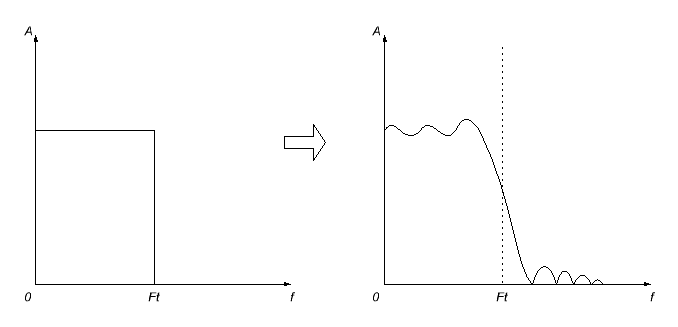
Pentru a minimiza aceste efecte, diferite funcții de netezire a ferestrei sunt aplicate răspunsului la impuls scurtat. Ca rezultat, răspunsul de frecvență este de obicei estompat și mai mult, dar oscilațiile neplăcute (mai ales în banda de trecere) dispar. 
De fapt, după o astfel de procesare, obținem un răspuns de impuls de funcționare și putem construi un filtru digital.
A doua metodă de calcul este și mai simplă - răspunsurile la impuls ale celor mai populare filtre au fost mult timp exprimate într-o formă analitică pentru noi. Rămâne doar să vă înlocuiți valorile și să aplicați o funcție de fereastră rezultatului după bunul plac. Deci nici măcar nu trebuie să numărați nicio transformare.
Și, bineînțeles, dacă obiectivul este de a imita comportamentul unui anumit circuit, puteți obține răspunsul său la impuls într-un simulator:

Aici am aplicat un impuls de 100500 volți (da, 100,5 kV) cu o durată de 1 μs la intrarea circuitului RC și am primit răspunsul la impuls. Este clar că în realitate acest lucru nu se poate face, dar în simulator, această metodă, după cum puteți vedea, funcționează excelent.
5. Note.
Cele de mai sus despre scurtarea răspunsului la impuls, desigur, s-au referit la așa-numitul. filtre de răspuns la impuls finit (filtre FIR / FIR). Au multe proprietăți valoroase, inclusiv faza liniară (în anumite condiții de răspuns la impuls), care nu dă nicio distorsiune a semnalului în timpul filtrării, precum și stabilitate absolută. Există, de asemenea, filtre cu răspuns de impuls infinit (filtre IIR / IIR). În ceea ce privește calculele, acestea consumă mai puține resurse, dar nu mai au avantajele enumerate.
În articolul următor, sper să vă arăt un exemplu simplu de implementare practică a unui filtru digital.
Prelegerea numărul 10
Filtre digitale cu răspuns la impulsuri finite
Funcția de transfer a unui filtru digital de răspuns la impuls finit realizabil fizic (filtru FIR) poate fi reprezentată ca
(10.1).
Când înlocuim în expresia (10.1), obținem răspunsul în frecvență al filtrului FIR în formă
![]() (10.2),
(10.2),
unde ![]() - caracteristică amplitudine-frecvență (AFC) filtru,
- caracteristică amplitudine-frecvență (AFC) filtru,
![]() - caracteristica frecvenței de fază (PFC) filtru.
- caracteristica frecvenței de fază (PFC) filtru.
Întârziere de fază filtru este definit ca
![]() (10.3).
(10.3).
Întârziere de grup filtru este definit ca
![]() (10.4).
(10.4).
O caracteristică distinctivă a filtrelor FIR este abilitatea de a implementa întârzieri constante de fază și grup în acestea, adică răspuns de fază liniară
(10.5),
unde un este o constantă. Dacă această condiție este îndeplinită, semnalul care trece prin filtru nu îi denaturează forma.
Pentru a obține condițiile care oferă un răspuns de fază liniar, scriem răspunsul de frecvență al filtrului FIR, luând în considerare (10.5)
![]() (10.6).
(10.6).
Echivalând părțile reale și imaginare ale acestei egalități, obținem
 (10.7).
(10.7).
Împărțind a doua ecuație la prima, obținem
 (10.8).
(10.8).
În cele din urmă, puteți scrie
 (10.9).
(10.9).
Această ecuație are două soluții. Primul laa \u003d 0 corespunde ecuației
 (10.10).
(10.10).
Această ecuație are o soluție unică corespunzătoare unui arbitrarh (0) (sin (0) \u003d 0) și h (n) \u003d 0 pentru n \u003e 0. Această soluție corespunde unui filtru al cărui răspuns la impuls are o singură contură diferită de zero la momentul inițial. Un astfel de filtru nu prezintă niciun interes practic.
Să găsim o altă soluție pentru. În acest caz, înmulțind încrucișător numeratorii și numitorii din (10.8), obținem
(10.11).
De aceea avem
![]() (10.12).
(10.12).
Deoarece această ecuație are forma unei serii Fourier, soluția sa, dacă există, este unică.
Este ușor de văzut că soluția la această ecuație trebuie să îndeplinească condițiile
(10.13),
(10.14).
Din condiția (10.13) rezultă că pentru fiecare ordine de filtrareN există o singură întârziere de fazăa , la care se poate realiza liniaritatea strictă a răspunsului de fază. Din condiția (10.14) rezultă că răspunsul la impuls al filtrului trebuie să fie simetric față de punctul pentru un imparN , și relativ la punctul de mijloc al intervalului (Figura 10.1).
 |
Răspunsul în frecvență al unui astfel de filtru (pentru un număr imparN ) poate fi scris ca
(10.15).
Efectuarea unei înlocuiri în a doua sumăm \u003d N -1- n, obținem
(10.16).
Deoarece h (n) \u003d h (N -1- n ), atunci cele două sume pot fi combinate
 (10.17).
(10.17).
Înlocuind, obținem
(10.18).
Dacă denotăm
 (10.19),
(10.19),
atunci putem scrie în cele din urmă
 (10.20).
(10.20).
Astfel, pentru un filtru cu răspuns de fază liniar, avem
 (10.21).
(10.21).
Pentru cazul egalN în mod similar vom avea
 (10.22).
(10.22).
Făcând o înlocuire în a doua sumă, obținem
 (10.23).
(10.23).
Făcând un înlocuitor, obținem
(10.24).
Prin desemnare
![]() (10.25),
(10.25),
va avea în sfârșit
 (10.26).
(10.26).
Astfel, pentru un filtru FIR cu un răspuns de fază liniar și o ordine uniformăN se poate scrie
 (10.27).
(10.27).
În cele ce urmează, pentru simplitate, vom lua în considerare doar filtrele cu o ordine ciudată.
La sintetizarea funcției de transfer a filtrului, parametrii inițiali sunt, de regulă, cerințele pentru răspunsul în frecvență. Există multe tehnici pentru sintetizarea filtrelor FIR. Să luăm în considerare unele dintre ele.
Deoarece răspunsul în frecvență al oricărui filtru digital este o funcție periodică a frecvenței, acesta poate fi reprezentat ca o serie Fourier
![]() (10.28),
(10.28),
unde sunt coeficienții seriei Fourier
 (10.29).
(10.29).
Se vede că coeficienții seriei Fourierh (n ) coincid cu coeficienții răspunsului la impulsul filtrului. Prin urmare, dacă este cunoscută o descriere analitică a răspunsului de frecvență necesar al filtrului, atunci este ușor să se determine coeficienții răspunsului la impuls și din acestea funcția de transfer a filtrului. Cu toate acestea, în practică acest lucru nu este fezabil, deoarece răspunsul la impuls al unui astfel de filtru are o lungime infinită. În plus, un astfel de filtru nu este realizabil din punct de vedere fizic, deoarece răspunsul la impuls începe de la -¥ , și nici o întârziere finită nu va face acest filtru realizabil fizic.
Una dintre metodele posibile pentru obținerea unui filtru FIR care aproximează un răspuns de frecvență dat este trunchierea seriei infinite Fourier și răspunsul la impuls al filtrului, presupunând căh (n) \u003d 0 pentru. Atunci
 (10.30).
(10.30).
Fezabilitatea fizică a funcției de transferH (z ) se poate realiza prin multiplicareH (z) pe.
 (10.31),
(10.31),
unde
(10.32).
Cu această modificare a funcției de transfer, caracteristica de amplitudine a filtrului nu se modifică, iar întârzierea grupului crește cu o valoare constantă.
De exemplu, să calculăm un filtru FIR low-pass cu un răspuns de frecvență al formularului
 (10.33).
(10.33).
În conformitate cu (10.29), coeficienții de răspuns la impulsul filtrului sunt descriși prin expresie
 (10.34).
(10.34).
Acum de la (10.31) se poate obține o expresie pentru funcția de transfer
 (10.35),
(10.35),
unde
(10.36).
Caracteristicile amplitudinii filtrului calculat pentru diverseN sunt prezentate în Figura 10.2.

Figura 10.2
Ondularea în banda de trecere și banda de stop se datorează convergenței lente a seriei Fourier, care, la rândul său, se datorează prezenței unei discontinuități în funcție la frecvența de întrerupere a benzii de trecere. Aceste valuri sunt cunoscute sub numele de gibbs ondulează.
Figura 10.2 arată că odată cu creștereaN frecvența de ondulare crește, iar amplitudinea scade atât la frecvențele inferioare, cât și la cele mai mari. Cu toate acestea, amplitudinea ultimei ondulații în banda de trecere și a primei ondulații din banda de oprire rămân practic neschimbate. În practică, astfel de efecte sunt adesea nedorite, ceea ce necesită găsirea unor modalități de reducere a pulsațiilor Gibbs.
Răspuns la impuls trunchiath (n ) poate fi reprezentat ca produsul răspunsului la impuls infinit necesar și unii funcțiile ferestrei w (n) de lungime n (Figura 10.3).
![]() (10.37).
(10.37).
 |
În cazul considerat al unei simple tăieri a seriei Fourier, folosim fereastră dreptunghiulară
 (10.38).
(10.38).
În acest caz, răspunsul în frecvență al filtrului poate fi reprezentat ca o convoluție complexă
 (10.39).
(10.39).
Aceasta înseamnă că va fi o versiune „neclară” a caracteristicii necesare.
Problema se reduce la găsirea funcțiilor ferestrei care pot reduce ondulația Gibbs cu aceeași selectivitate a filtrului. Pentru a face acest lucru, trebuie mai întâi să studiați proprietățile funcției ferestrei folosind exemplul unei ferestre dreptunghiulare.
Spectrul funcției de fereastră dreptunghiulară poate fi scris ca
 (10.40).
(10.40).
Spectrul funcției de fereastră dreptunghiulară este prezentat în Figura 10.4.

Figura 10.4
Din moment ce, lățimea lobului principal al spectrului se dovedește a fi.
Prezența lobilor laterali în spectrul funcției ferestrei duce la o creștere a ondulației Gibbs în răspunsul de frecvență al filtrului. Pentru a obține o ondulație mică în banda de trecere și o atenuare mare în banda de oprire, este necesar ca aria delimitată de lobii laterali să fie o mică fracțiune din aria delimitată de lobul principal.
La rândul său, lățimea lobului principal determină lățimea zonei de tranziție a filtrului rezultat. Pentru selectivitate ridicată a filtrului, lățimea lobului principal ar trebui să fie cât mai mică posibil. După cum se vede din cele de mai sus, lățimea lobului principal scade odată cu creșterea ordinii filtrului.
Astfel, proprietățile funcțiilor de fereastră adecvate pot fi formulate după cum urmează:
- funcția de fereastră trebuie să fie limitată în timp;
- spectrul funcției de fereastră ar trebui să se apropie cel mai bine de funcția limitată în frecvență, adică să aibă un minim de energie în afara lobului principal;
- lățimea lobului principal al spectrului funcției ferestrei ar trebui să fie cât mai mică posibil.
Cele mai utilizate funcții ale ferestrei sunt:
1. Fereastra dreptunghiulară. Considerat mai sus.
2. Fereastra cu ciocan.
 (10.41),
(10.41),
unde.
Când această fereastră se numește fereastra lui Henn (hanning).
3. Fereastra Blackman.
 (10.42).
(10.42).
4. Fereastra Bartlett.
 (10.43).
(10.43).
Indicatorii filtrelor construite folosind funcțiile ferestrei indicate sunt rezumate în Tabelul 10.1.
|
Fereastră |
Lățimea lobului principal |
Factor de ondulare,% |
||
N \u003d 11 |
N \u003d 21 |
N \u003d 31 |
||
|
Dreptunghiular |
22.34 |
21.89 |
21.80 |
|
|
Hanning |
2.62 |
2.67 |
2.67 |
|
|
Hamming |
1.47 |
0.93 |
0.82 |
|
|
Om negru |
0.08 |
0.12 |
0.12 |
|
Factorul de ondulare este definit ca raportul dintre amplitudinea maximă a lobului lateral și amplitudinea lobului principal în spectrul funcției ferestrei.
Pentru a selecta ordinea de filtrare necesară și cea mai potrivită funcție de fereastră la calcularea filtrelor reale, puteți utiliza datele din Tabelul 10.2.
|
tranzitorie |
Denivelări transmisie (dB) |
Atenuarea în bariere (dB) |
|
|
Dreptunghiular |
|||
|
Hanning |
|||
|
Hamming |
|||
|
Om negru |
După cum se poate vedea din Tabelul 10.1, există o relație clară între factorul de ondulare și lățimea lobului principal în spectrul funcției ferestrei. Cu cât este mai mic coeficientul de ondulare, cu atât este mai mare lățimea lobului principal și, prin urmare, zona de tranziție în răspunsul de frecvență al filtrului. Pentru a asigura o ondulație scăzută în banda de trecere, este necesar să alegeți o fereastră cu un coeficient de ondulare adecvat și să asigurați lățimea necesară a zonei de tranziție cu un ordin de filtrare crescut N.
Această problemă poate fi rezolvată folosind fereastra sugerată de Kaiser. Funcția fereastră Kaiser are forma
 (10.44),
(10.44),
unde a este un parametru independent, ![]() , I 0 este funcția Bessel de ordinul zero de primul fel, definită de expresie
, I 0 este funcția Bessel de ordinul zero de primul fel, definită de expresie
 (10.45).
(10.45).
O proprietate atractivă a ferestrei Kaiser este capacitatea de a modifica fără probleme coeficientul de ondulare de la valori mici la valori mari atunci când se schimbă doar un parametru a. În acest caz, ca și pentru alte funcții ale ferestrei, lățimea lobului principal poate fi controlată prin ordinea filtrului N.
Parametrii principali stabiliți la dezvoltarea unui filtru real sunt:
Lățime de bandă - w p;
Banda de obstacole - w a;
Ridicarea maximă admisibilă în banda de trecere - A p;
Atenuare minimă în banda de oprire - A a;
-frecvența de eșantionare -w s.
Acești parametri sunt ilustrați în Figura 10.5. În acest caz, ondularea maximă în banda de trecere este definită ca
![]() (10.46),
(10.46),
și atenuarea minimă în banda de oprire ca
O procedură relativ simplă pentru calcularea unui filtru cu o fereastră Kaiser include următorii pași:
1. Răspunsul la impuls al filtrului h (n) este determinat cu condiția ca răspunsul în frecvență să fie ideal
 (10.48),
(10.48),
unde (10.49).
2. Parametrul d este selectat ca
![]() (10.50),
(10.50),
unde  (10.51).
(10.51).
3. Adevărata valoare a A a și A p se calculează prin formulele (10.46), (10.47).
4. Alegeți parametrul a as
 (10.52).
(10.52).
5. Selectați parametrul D ca
 (10.53).
(10.53).
6. Cea mai mică valoare impar a ordinii filtrului este selectată din condiție
![]() (10.54),
(10.54),
 (10.57)
(10.57)
urmează că
Deoarece eșantioanele răspunsului la impuls ale filtrului sunt coeficienții funcției sale de transfer, condiția (10.59) înseamnă că codurile tuturor coeficienților filtrului conțin doar o parte fracționată și un bit de semn și nu conțin o parte întreagă.
Numărul de biți ai părții fracționate a coeficienților filtrului este determinat din condiția de a satisface funcția de transfer a filtrului cu coeficienți cuantizați, cerințele specificate pentru aproximarea la funcția de transfer de referință cu valorile exacte ale coeficienților.
Valorile absolute ale eșantioanelor semnalelor de intrare ale filtrului sunt de obicei normalizate astfel încât
Dacă analiza se efectuează pentru un filtru FIR cu răspuns de fază liniar, algoritmul pentru calcularea semnalului de ieșire poate fi după cum urmează
unde sunt coeficienții filtrului rotunjiți la s k.
Diagrama bloc a filtrului prezentată în Fig. 10.5 corespunde acestui algoritm.
 |
Există două moduri de a implementa acest algoritm. În primul caz, toate operațiile de multiplicare sunt executate exact și nu există rotunjiri ale produselor. În acest caz, lungimea cuvântului produselor este egală cu s în + s k, unde s in este lățimea semnalului de intrare și s k este lățimea coeficienților filtrului. În acest caz, diagrama bloc a filtrului prezentată în Fig. 10.5 corespunde exact filtrului real.
În al doilea mod de implementare a algoritmului (10.61), fiecare rezultat al operației de multiplicare este rotunjit, adică produsele sunt calculate cu o anumită eroare. În acest caz, este necesar să se schimbe algoritmul (10.61) astfel încât să se ia în considerare eroarea introdusă prin rotunjirea produselor
Dacă valorile eșantionului semnalului de ieșire al filtrului sunt calculate conform primei metode (cu valorile exacte ale produselor), atunci varianța zgomotului de ieșire este determinată ca
![]() (10.66),
(10.66),
acestea. depinde de varianța zgomotului rotund al semnalului de intrare și de valorile coeficienților filtrului. De aici puteți găsi numărul necesar de biți ai semnalului de intrare ca
 (10.67).
(10.67).
Din valorile cunoscute ale lui s și k, se poate determina numărul de biți necesari pentru partea fracțională a codului semnalului de ieșire ca
Dacă valorile eșantionului semnalului de ieșire sunt calculate în conformitate cu a doua metodă, când fiecare produs este rotunjit la s d biți, atunci varianța zgomotului de rotunjire generat de fiecare dintre multiplicatori poate fi exprimată în termeni de lățime a produsului
DR in și raportul semnal-zgomot la ieșirea SNR a filtrului. Valoarea intervalului dinamic al semnalului de intrare în decibeli este definită ca
![]() (10.74),
(10.74),
unde A max și A min sunt amplitudinile maxime și minime ale semnalului de intrare al filtrului.
Raportul semnal-zgomot la ieșirea filtrului, exprimat în decibeli, este definit ca
![]() (10.75),
(10.75),
determină valoarea rădăcină-medie-pătrat a puterii semnalului sinusoidal de ieșire al filtrului cu amplitudinea A min și
(10.77)
determină puterea de zgomot la ieșirea filtrului. Din (10.75) și (10.76) cu A max \u003d 1 obținem o expresie pentru varianța zgomotului de ieșire al filtrului
![]() (10.78).
(10.78).
Această valoare a varianței zgomotului de ieșire al filtrului poate fi utilizată pentru a calcula lățimile semnalelor de intrare și ieșire ale filtrului.
Să luăm în considerare cel mai simplu dintre filtrele digitale - filtre cu parametri constanți.
Semnalul de intrare este alimentat la intrarea filtrului digital sub forma unei secvențe de valori numerice care urmează cu un interval (Fig. 4.1, a). Când fiecare valoare următoare a semnalului ajunge în filtrul digital, se calculează următoarea valoare a semnalului de ieșire. Algoritmii de calcul pot fi foarte diversi; în timpul calculului, pe lângă ultima valoare a semnalului de intrare,
valori anterioare ale semnalelor de intrare și ieșire: Semnalul de la ieșirea filtrului digital este, de asemenea, o succesiune de valori numerice, urmând un interval. Acest interval este același pentru întregul dispozitiv de procesare a semnalului digital.

Figura: 4.1. Semnal la intrarea și ieșirea filtrului digital
Prin urmare, dacă cel mai simplu semnal este aplicat la intrarea filtrului digital sub forma unui singur impuls (Fig. 4.2, a)
![]()
apoi la ieșire obținem un semnal sub forma unei secvențe discrete de valori numerice, urmând un interval
Prin analogie cu circuitele analogice convenționale, numim acest semnal de răspuns răspunsul la impulsul filtrului (Fig. 4.2, b). Spre deosebire de răspunsul la impuls al unui circuit analogic, funcția este adimensională.

Figura: 4.2. Răspuns la impuls unic și filtru digital
Să aplicăm un semnal discret arbitrar la intrarea filtrului Fig. 4.1, a), care este un set de valori discrete
Sub acțiunea primului element la ieșirea filtrului, se formează o secvență înmulțită cu secvența înmulțită cu și deplasată la dreapta cu o cantitate etc. Ca rezultat, la ieșire, obținem o secvență cu

Astfel, semnalul de ieșire este definit ca o convoluție discretă a semnalului de intrare și a răspunsului la impuls. În acest sens, filtrele digitale sunt similare cu circuitele convenționale, unde ieșirea este egală cu convoluția intrării și a răspunsului la impuls.
Formula (4.1) este un algoritm de filtrare digitală. Dacă răspunsul la impuls al filtrului este descris de o secvență cu un număr finit de membri, atunci filtrul poate fi implementat ca un circuit prezentat în Fig. 4.3. Aici litera denotă elementele întârzierii semnalului pentru un timp (pe o celulă) -elemente care multiplică semnalul cu factorul corespunzător.
Circuitul prezentat în Fig. 4.3 nu este o schemă de cablare a filtrului digital; această diagramă este o reprezentare grafică a algoritmului de filtrare digitală și arată secvența operațiilor aritmetice efectuate în timpul procesării semnalului.

Figura: 4.3. Circuit de filtru digital non-recursiv
Pentru filtrele digitale care procesează semnale sub formă de secvențe numerice abstracte, conceptul de „întârziere în timp” nu este în totalitate corect. Prin urmare, elementele care întârzie semnalul pe o celulă sunt de obicei marcate pe circuitele de filtrare digitale cu un simbol care denotă întârzierea semnalului în limbajul transformărilor. În cele ce urmează, vom adera la această desemnare.
Să ne întoarcem la circuitul de filtrare digital prezentat în Fig. 4.3 Filtrele care utilizează numai valori ale semnalului de intrare pentru calcul se numesc simple sau nerecursive.
Un algoritm de filtru nerecursiv este ușor de scris dacă este cunoscut răspunsul la impuls al filtrului. Pentru implementarea practică a algoritmului, este necesar ca răspunsul la impuls să conțină un număr finit de termeni. Dacă răspunsul la impuls conține un număr infinit de termeni, dar acestea scad rapid în mărime, atunci ne putem limita la un număr finit de termeni, aruncându-i pe cei ale căror valori sunt mici. Dacă elementele răspunsului la impuls nu scad în mărime, algoritmul filtrului nerecursiv se dovedește a fi irealizabil.

Figura: 4.4. -lanţ
Ca exemplu, luați în considerare cel mai simplu filtru digital similar cu lanțul (Fig. 4.4). Răspunsul la impuls al lanțului are forma
![]()
Pentru a scrie răspunsul la impuls al filtrului digital corespunzător, expresia ar trebui înlocuită cu Cu toate acestea, răspunsul la impuls al lanțului este adimensional și răspunsul la impuls al filtrului digital trebuie să fie adimensional. Prin urmare, omitem factorul din expresie (4.2) și scriem răspunsul la impuls al filtrului digital în formă
![]()
Un astfel de răspuns de impuls conține infinit de mulți termeni, dar valoarea lor scade exponențial și vă puteți limita la termeni, alegând astfel încât
Acum puteți scrie o expresie pentru semnal la ieșirea filtrului
Această expresie este, de asemenea, un algoritm de filtrare digitală. Diagrama acestui filtru este prezentată în Fig. 4.5.
A doua abordare a analizei proceselor în filtrele digitale este similară cu metoda operatorului de analiză a circuitelor analogice convenționale, doar că în locul transformatei Laplace se folosește -transforma.

Figura: 4.5. Diagrama unui filtru digital non-recursiv similar cu -chain
Să definim parametrul filtrului digital, similar cu funcția de transfer a circuitului electric. Pentru a face acest lucru, aplicați -conversia la răspunsul la impuls al filtrului digital:

Funcția se numește funcția de filtrare a sistemului.
În conformitate cu expresia (4.1), semnalul de la ieșirea filtrului digital este egal cu convoluția discretă a semnalului de intrare și răspunsul la impuls al filtrului. Aplicând teorema transformării convoluției la această expresie, obținem că -transformarea semnalului de ieșire este egală cu -transformarea semnalului de intrare înmulțit cu funcția de filtrare a sistemului:
![]()
Astfel, funcția de sistem joacă rolul funcției de transfer al filtrului digital.
De exemplu, să găsim funcția de sistem a unui filtru digital de ordinul întâi similar cu -chain:

A treia metodă de analiză a trecerii semnalelor prin filtrele digitale este similară cu metoda clasică a ecuațiilor diferențiale. Să luăm în considerare această metodă folosind exemplul lanțurilor de ordine.
Cel mai simplu circuit analogic de ordinul 1 este un lanț (a se vedea figura 4.4), trecerea semnalelor prin care este descrisă prin ecuația diferențială
![]()
Pentru un circuit discret, în loc de ecuația diferențială (4.8), ar trebui să se scrie o ecuație a diferenței, în care semnalele de intrare și ieșire sunt specificate pentru momente discrete de timp și diferența valorilor semnalului adiacente ar trebui să apară în locul derivatei. Pentru un lanț discret de ordinul 1, ecuația diferenței poate fi scrisă într-o formă destul de generală
Aplicăm ecuației -transformare
de unde găsim funcția de filtrare a sistemului
![]()
Formula (4.10) este o expresie destul de generală pentru funcția de sistem a filtrului digital de ordinul 1. Când coincide cu expresia obținută anterior (4.7) pentru funcția de sistem a filtrului digital, care este echivalentă cu -lantul.
Să găsim algoritmul de filtrare digitală corespunzător funcției de sistem (4.10). Pentru aceasta, rezolvăm ecuația (4.9) cu privire la
Un circuit echivalent al acestui algoritm este prezentat în Fig. 4.6. Comparativ cu filtrul nerecursiv (vezi Fig. 4.5), aici s-a adăugat un fel de "buclă de feedback", ceea ce înseamnă că valorile semnalului de ieșire sunt utilizate în următoarele

Figura: 4.6. Schema unui filtru digital recursiv similar unui lanț
calcule. Filtrele de acest tip se numesc recursive.
Algoritmul (4.11) corespunde unui filtru care este complet echivalent cu filtrul nerecursiv considerat anterior. Dar pentru a determina o valoare a semnalului de ieșire utilizând algoritmul de filtru non-recursiv (4.4), este necesar să efectuați operațiuni, iar atunci când utilizați algoritmul de filtru recursiv (4.11), sunt necesare doar două operații. Acesta este principalul avantaj al filtrelor recursive. În plus, filtrele recursive permit procesarea semnalului cu o precizie mai mare, deoarece permit implementarea mai corectă a răspunsului la impuls fără a arunca „coada” acestuia. Filtrele recursive vă permit să implementați algoritmi care în general nu sunt posibili cu filtrele non-recursive. De exemplu, cu un filtru care funcționează conform schemei din Fig. 4.6, este, în esență, un acumulator-integrator ideal și are un răspuns de impuls al formei. Un filtru cu o astfel de caracteristică nu poate fi implementat într-un circuit nerecursiv.
Exemplele luate în considerare arată că nu are sens să se aplice algoritmi nerecursivi pentru a crea filtre digitale cu un răspuns impuls lung. În aceste cazuri, este mai logic să folosiți filtre recursive.
Domeniul de aplicare pentru algoritmi nerecursivi este implementarea filtrelor digitale cu un număr mic de termeni de răspuns la impuls. Un exemplu este un diferențiator simplu al cărui semnal de ieșire este egal cu creșterea semnalului de intrare:
Diagrama unui astfel de filtru digital este prezentată în Fig. 4.7.

Figura: 4.7. Diagrama celui mai simplu diferențiator digital
Luați în considerare acum un filtru digital general, care este descris de ecuație
Această ecuație poate fi considerată atât ca o ecuație a diferenței de ordine, cât și ca un algoritm de filtrare digitală, dacă o rescriem diferit, și anume

Figura: 4.8. Circuit de filtru de comandă digitală recursiv
Algoritmul (4.13) corespunde schemei prezentate în Fig. 4.8. Să găsim funcția de sistem a unui astfel de filtru. Pentru a face acest lucru, aplicați ecuației -transformare:
Expresia (4.14) permite stabilirea unei conexiuni între oscilațiile elementelor circuitului de filtrare și funcția sistemului. Coeficienții din numeratorul funcției sistemului determină valorile coeficienților la
(în partea non-recursivă a filtrului), iar coeficienții din numitor definesc partea recursivă a filtrului.
48 Filtre digitale cu răspuns de impuls finit. Calculul filtrelor de tac.
Filtru de răspuns de impuls finit (Filtru nerecursiv, Filtru FIR) sau FIR-filter (abrevierea FIR pentru răspunsul la impuls finit) - unul dintre tipurile de filtre digitale liniare, a cărui caracteristică este răspunsul său la impuls limitat în timp (de la un moment dat devine exact zero). Un astfel de filtru este, de asemenea, numit non-recursiv din cauza lipsei de feedback. Numitorul funcției de transfer a unui astfel de filtru este o anumită constantă.
Ecuația diferenței care descrie relația dintre semnalele de intrare și de ieșire ale filtrului: unde P- ordinea filtrului, x(n) - semnal de intrare, y(n) este semnalul de ieșire și b eu - coeficienți de filtrare. Cu alte cuvinte, valoarea oricărui eșantion al semnalului de ieșire este determinată de suma valorilor scalate Pmostre anterioare. Se poate spune diferit: valoarea ieșirii filtrului în orice moment este valoarea răspunsului la valoarea instantanee a intrării și suma tuturor răspunsurilor amortizate treptat Pmostre de semnal anterioare care afectează încă ieșirea (după P-conturi, funcția tranzitorie de impuls devine egală cu zero, așa cum am menționat deja, prin urmare, toți termenii după Pa devenit, de asemenea, egal cu zero). Să scriem ecuația anterioară într-o formă mai încăpătoare:

Pentru a găsi nucleul filtrului, puneți
x(n) = δ( n)
unde δ ( n) este o funcție delta. Apoi răspunsul la impuls al filtrului FIR poate fi scris ca:

Transformarea Z a răspunsului la impuls ne oferă funcția de transfer a filtrului FIR:

] Proprietăți
Un filtru FIR are o serie de proprietăți utile care îl fac uneori mai preferabil de utilizat decât un filtru IIR. Iată câteva dintre ele:
Filtrele FIR sunt robuste.
Filtrele FIR nu necesită feedback atunci când sunt implementate.
Faza filtrelor FIR poate fi făcută liniară
Filtru direct de tip FIR
Filtrele FIR pot fi implementate folosind trei elemente: un multiplicator, un sumator și o unitate de întârziere. Varianta prezentată în figură este o implementare directă a filtrelor FIR de tip 1.

Implementarea directă a filtrului FIR
Program de probă
Următorul este un exemplu de program de filtrare FIR scris în C:
/ * Filtru FIR pentru 128 de atingeri * /
float fir_filter (intrare float)
eșantion static plutitor;
acc \u003d 0,0f; /* Baterie */
/ * Multiplicare și acumulare * /
pentru (i \u003d 0; i< 128; i++) {
acc + \u003d (h [i] * eșantion [i]);
/ * Ieșire * /
/ * Compensați semnalul întârziat * /
pentru (i \u003d 127; i\u003e 0; i--)
sample [i] \u003d eșantion;
49 Netezirea datelor. Medie mobilă.
50 Netezirea datelor. Netezirea cu parabole.
51 Netezirea datelor. Netezire Spencer.
52 Netezirea datelor. Filtrarea mediană.
Medierea în mișcare, netezirea de către iepuri, netezirea Spencer, filtrarea mediană
Atunci când se dezvoltă metode pentru determinarea parametrilor proceselor fizice care variază lent în timp, o sarcină importantă este eliminarea influenței efectelor de zgomot sau a interferențelor aleatorii care se suprapun asupra semnalului procesat primit la ieșirea convertorului primar.
Pentru a elimina acest efect, puteți aplica netezirea datelor. Una dintre cele mai simple modalități de a face acest lucru este media aritmetică. Când este aplicată, fiecare valoare a unei funcții discrete (matrice de date procesate) este calculată în conformitate cu expresia:
unde este numărul de puncte pentru media aritmetică (număr impar);
Valoarea funcției trecută înainte de procesare;
Există, de asemenea, alte metode destul de eficiente de netezire, de exemplu, prin parabole de gradul al doilea la cinci, șapte, nouă și unsprezece puncte, în conformitate cu expresiile:
sau parabole de gradul al patrulea la șapte, nouă, unsprezece și treisprezece puncte:
În aplicații practice, alte metode eficiente dau rezultate bune, de exemplu, netezirea Spencer în 15 puncte:
Înlocuind un exponent complex în aceste expresii, unde puteți determina funcția de transfer a transformării corespunzătoare.
Pentru media aritmetică
Expresia dintre paranteze este o progresie geometrică cu un numitor, prin urmare, această expresie poate fi reprezentată ca:
 .
.
Această formulă reprezintă caracteristica de transfer a filtrului trece-jos și se poate vedea din acesta că, cu cât sunt implicați mai mulți termeni în mediere, cu atât este mai mare suprimarea componentelor de zgomot de înaltă frecvență din semnal (vezi Figura 6.1).
Cu toate acestea, conceptul de frecvență la procesarea tendințelor de timp diferă de conceptul analog la procesarea semnalelor. Acest lucru se datorează faptului că atunci când studiați tendințele de timp, nu compoziția lor de frecvență este de interes, ci tipul de schimbare (creștere, scădere, constanță, ciclicitate etc.).
Utilizarea așa-numiților algoritmi euristici este, de asemenea, destul de eficientă pentru netezirea datelor.
Una dintre ele este filtrarea mediană. În cursul implementării sale într-o fereastră de timp glisantă a dimensiunii, în care un număr întreg este un număr impar, elementul central este înlocuit cu elementul de mijloc al secvenței, care sunt ordonate, în ordine crescătoare a valorilor, elemente din matricea de date a semnalului netezit care se încadrează în fereastra de timp. Avantajul filtrării mediane este capacitatea de a elimina zgomotul de impuls, a cărui durată nu depășește, practic fără a distorsiona semnalele care se schimbă ușor. Această metodă de suprimare a zgomotului nu are o justificare matematică riguroasă, dar simplitatea calculelor și eficiența rezultatelor obținute au condus la utilizarea sa pe scară largă.

Figura 6.1 - Grafice ale caracteristicilor de transfer
operații de calcul aritmetic pentru m \u003d 5, 7, 9, 11
Un alt algoritm de netezire interesant este medierea mediană. Esența sa este următoarea. Într-o fereastră de timp glisantă, dimensiunile (- un număr întreg ciudat), elementele matricei de date sunt ordonate în ordine crescătoare, iar apoi primul și ultimul element sunt eliminate din secvența ordonată (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Această metodă vă permite să suprimați interferențele de impulsuri și frecvențe radio, precum și să obțineți o bună netezire a semnalului.
| " |




