1st course, Higher Mathematics, we study matrians and basic actions on them. Here we systematize the basic operations that can be carried out with matrices. How to start an acquaintance with matrices? Of course, with the simplest - definitions, basic concepts and simplest operations. We assure the matrices will understand everything who will give them at least a little time!
Definition of the matrix
The matrix - This is a rectangular table of elements. Well, if a simple language is a table of numbers.
Usually matrices are designated by capital latin letters. For example, the matrix A. , the matrix B. etc. The matrices can be of different sizes: rectangular, square, there are also matrices strings and column matrices, called vectors. The size of the matrix is \u200b\u200bdetermined by the number of rows and columns. For example, write a rectangular size matrix m. on the n. where m. - number of lines, and n. - Number of columns.
Elements for which i \u003d j. (a11, A22, .. ) Forming the main diagonal of the matrix, and are called diagonal.
What can be done with matrices? Fold / deduct, multiply by number, multiply among themselves, transpose. Now about all these basic operations over matrices in order.
Operations of addition and subtraction of matrices
Immediately warned that you can add only matrices of the same size. As a result, the matrix of the same size will be. To fold (or deduct) the matrix is \u200b\u200bsimple - just folded their corresponding elements . Let us give an example. Perform the addition of two matrices A and in two two.
Subtraction is performed by analogy, only with the opposite sign.
You can multiply any matrix on an arbitrary number. To do this, you need to multiply by this number each element. For example, multiply the matrix A from the first example number 5:
Multiplication operation Matrix
Not all matrices will be possible to multiply. For example, we have two matrices - a and b. They can be multiplied by each other only if the number of columns of the matrix is \u200b\u200bas equal to the number of lines of the matrix B. At the same time each element of the resulting matrix, standing in the i-th row and the J-M column, will be equal to the amount of products of the corresponding elements in the first line of the first factor and the J-M column of the second. To understand this algorithm, write down, as two square matrices are multiplied:
And an example with real numbers. Multiply matrix:
Transposing Operation Matrix
The transposition of the matrix is \u200b\u200ban operation when the corresponding lines and columns are changed in places. For example, we transpose matrix A from the first example:
The determinant of the matrix
The determinant, about the determinant - one of the basic concepts of a linear algebra. Once people came up with linear equations, and the determinant had to invent them. As a result, you have to deal with all this, so, the last jerk!
The determinant is the numerical characteristic of the square matrix that is needed to solve many tasks.
To calculate the determinant of the simplest square matrix itself, it is necessary to calculate the difference in the works of the elements of the main and side diagonals.
The determinant of the first order matrix, that is, consisting of one element is equal to this element.
And if the matrix is \u200b\u200bthree to three? It is already more complicated here, but you can cope.
For such a matrix, the value of the determinant is equal to the amount of products of the elements of the main diagonal and the works of the elements of the triangles with the line of the parallel main diagonal, on which the product of the elements of the side diagonal and the product of the elements lying on triangles with the facet parallel to diagonal are subtracted.
Fortunately, to calculate the determinants of large-sized matrices in practice are rare.
Here we looked at the basic operations on matrices. Of course, in real life, it is never possible to meet even a hint of a matrix system of equations or vice versa - encounter much more complex cases when you have to really break your head. It is for such cases that there is a professional student service. Contact help, get a high-quality and detailed solution, enjoy learning and free time.
Lecture #1.
Matrians
Definition and types of matrices
Definition 1.1.Matrixsize t. pcalled a rectangular table of numbers (or other objects) containing m.rows I. n.columns.
The matrices are designated (capitalized) letters of the Latin alphabet, for example, A, B, C, ...Numbers (or other objects), component matrix, are called elementsmatrix. The elements of the matrix can be functions. To denote the elements of the matrix, the lowercase letters of the Latin alphabet with double indexing are used: aijwhere the first index is i.(read - and) - Row number, second index j.(read - zh) – column number.
Definition 1.2.The matrix is \u200b\u200bcalled square p-order, if the number of its rows is equal to the number of columns and equally the same number p
Concepts are introduced for a square matrix main and adversediagonal.
Definition 1.3.Home Diagonalthe square matrix consists of elements having the same indexes, i.e.. These are items: a.11, A 22, ...
Definition 1.4. diagonalif all the elements except the elements of the main diagonal are zero
Definition 1.5.Square matrix is \u200b\u200bcalled triangularIf all its elements below (or higher) the main diagonal are zero.
Definition 1.6.Square matrix p-order, in which all elements of the main diagonal are equal to one, and the rest are zero, called singlematrix n.-o order and it is indicated by the letter E.
Definition 1.7.The matrix of any size is called ,or zero matrixif all its elements are zero.
Definition 1.8.The matrix consisting of one line is called matrix row.
Definition 1.9.The matrix consisting of one column is called column matrix.
A \u003d (a11 but12 ... but1n) -string matrix;
Definition 1.10.Two matrices BUTand INidentical sizes called equalif all the respective elements of these matrices are equal, i.e. aij \u003d Bij.for anyone i.= 1, 2, ..., t; J \u003d.1, 2,…, n..
Operations on matrices
Over the matrices, as over the numbers, you can produce a number of operations. The main operations over the matrices are the addition (subtraction) of matrices, multiplying the matrix to the number, multiplication of matrices. These operations are similar to operations over numbers. Specific operation - transposition of the matrix.
Multiplication of the matrix to the number
Definition 1.11.The work of the matrix and the numberλ is called the matrix In \u003d a,elements of which are obtained by multiplying elements mat rice BUTby number λ. .
Example 1.1.Find the work of the matrix A \u003d. 
Number 5.
Decision. .◄ 5A \u003d. 
Multiplication rule matrix by number: To multiply the matrix to the number, you must multiply on this number all the elements of the matrix.
Corollary.
1. The total multiplier of all the elements of the matrix can be taken out for the sign of the matrix.
2. Work of the matrix BUTby number 0 there is a zero matrix: BUT· 0 = 0 .
Addition of matrices
Definition 1.12.The sum of two matrices A and insame size t N.called the matrix FROM= BUT+ INwhose elements are obtained by the addition of the corresponding elements of the matrix BUTand matrix IN, i.e. cij \u003d Aij + Bijfor i \u003d.1, 2, ..., m.; j.= 1, 2, ..., n.(i.e., the matrices are addressed alternately).
Corollary.The amount of the matrix BUTwith a zero matrix is \u200b\u200bequal to the original matrix: A + O \u003d A.
1.2.3. Subtraction of matrices
The difference of two matricesthe same size is determined through the pre-operating operations: A - B \u003d a + (-1)IN.
Definition 1.13.The matrix -A \u003d (-1)BUTcalled oppositematrix BUT.
Corollary.The sum of opposite matrices is equal to a zero matrix : A + (-a) \u003d O.
Matrix multiplication
Definition 1.14.Multiplication of the matrix A on the matrix init is determined when the number of columns of the first matrix is \u200b\u200bequal to the number of rows of the second matrix. Then work of matricesthis matrix is \u200b\u200bcalled , each element of which cij.equal to the amount of works of elements i.- Lines of the matrix BUTon the appropriate elements j.-to column of the matrix B.
Example 1.4.Calculate the work of matrices A · in,where
A \u003d. 
= 
Example 1.5.Find works by Matrix AUand Vawhere
Comments.From examples 1.4-1.5 it follows that the multiplication of matrices has some differences from multiplication of numbers:
1) if the work of the matrices AUthere is, then after rearrangement of the factors in places the work of matrices V.may not exist. Indeed, in example 1.4, the product of AB matrices exists, and the product of wa no exists;
2) if even works AUand V.there are, the result of the work may be matrices of different sizes. In the case when both works AUand V.there are both both matrices of the same size (this is possible only when multiplying the square matrices of one order), commutative (moving) the law of multiplication is still not performed,those. A B. In a, as in Example 1.5;
3) However, if you multiply a square matrix BUTon a single matrix E.of the same order then AE \u003d EA \u003d A.
Thus, a single matrix when multiplying matrices plays the same role as the number 1 with multiplication of numbers;
4) the product of two non-zero matrices can be equal to a zero matrix, i.e. from the fact that A B.\u003d 0, it does not follow that A \u003d.0 or B \u003d.0.
This methodological manual will help you learn to perform actions with matrices: addition (subtraction) of matrices, transpose matrix, multiplication of matrices, finding the reverse matrix. All material is set forth in a simple and accessible form, appropriate examples are given, so even an unprepared person will be able to learn to perform actions with matrices. For self-control and self-test you can download the Matrix Calculator for free \u003e\u003e\u003e.
I will try to minimize theoretical calculations, in some places, explanations "on the fingers" and the use of unscientific terms. Lovers of a solid theory, please do not criticize, our task is learn to perform action with matrices.
For ultra-fast preparation on the topic (who has "burning") there is an intense PDF course Matrix, determinant and standing!
The matrix is \u200b\u200ba rectangular table of any elements. As elements We will consider numbers, that is, numerical matrices. ELEMENT - This is the term. The term is advisable to remember, it will often meet, it's not by chance that I used a fat font to highlight it.
Designation: Matrices usually denote by capital latin letters
Example: Consider the "Two Three" matrix:
This matrix consists of six elements:
All numbers (elements) inside the matrix exist in themselves, that is, no deduction of speech does not go: 
It's just a table (set) numbers!
Also agree do not rearrange Numbers, unless otherwise mentioned. Each number has its own location, and they cannot be pulled out!
The matrix under consideration has two lines: 
And three columns: 
STANDARD: When they talk about the sizes of the matrix, then first Indicate the number of rows, and only then - the number of columns. We have just disassembled the bones of the "Two Three" matrix.
If the number of rows and columns of the matrix coincides, then the matrix is \u200b\u200bcalled square, eg: 
- Matrix "Three Three".
If in the matrix one column or one line, then such matrices are also called vectors.
In fact, the concept of the matrix, we know from school, consider, for example, a point with the "X" coordinates and "igrek" :. Essentially, the coordinates of the point are recorded in the "one-two" matrix. By the way, here's the example, why the order of numbers is important: and are two completely different points of the plane.
Now go directly to the study actions with matrixes:
1) The first action. Reaching minus from the matrix (making a minus in the matrix).
Return to our Matrix 
. As you probably noticed, there are too many negative numbers in this matrix. It is very uncomfortable in terms of performing various actions with the matrix, it is inconvenient to write as many minuses, and just looks ugly in the design.
I will make minus beyond the matrix, changing each element of the matrix sign:
Ulya, as you understand, the sign does not change, zero - he and in Africa zero.
Feed example: 
. Looks ugly.
We will make a minus in the matrix, changing the matrix of each element:
Well, it turned out much more prettier. And, most importantly, perform any actions with the matrix will be easier. Because there is such a mathematical folk sign: the more minuses - the more confusion and mistakes.
2) Action second. Multiplication of the matrix to the number.
Example:
Everything is simple in order to multiply the matrix on the number, you need everyone Matrix element multiply to a given number. In this case, on the top three.
Another useful example:
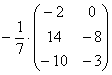- multiplication of the matrix for the fraction
First consider what to do DO NOT:
You do not need to enter the matrix, firstly, it only makes it difficult for further action with the matrix, secondly, it makes it difficult to check the decision by the teacher (especially if 
- Final answer answer).
And especially, DO NOT Share each element of the matrix for minus seven:
From the article Mathematics for dummies or starting to startWe remember that decimal fractions with a comma in higher mathematics are trying to avoid every way.
The only thing that desirable Make in this example - to make a minus in the matrix:
But if EVERYTHING The elements of the matrix were divided into 7 without residuethen you can (and you need!) It would be divided.
Example:
In this case, you can and NEED TO Multiply all the elements of the matrix on, since all the numbers of the matrices are divided into 2 without residue.
Note: In the theory of higher mathematics, the school concept "division" is not. Instead of the phrase "this is divided into it" can always be said "multiply by fraction." That is, division is a special case of multiplication.
3) the third action. Transposing the matrix.
In order to transpose the matrix, you need to write its lines to the column of the transposed matrix.
Example:
Transpose matrix
The line here is only one and, according to the rule, it needs to be written to the column:
- Transposed matrix.
The transposed matrix is \u200b\u200busually denoted by a sudden index or a touch at the top.
Step by step example:
Transpose matrix 
First, rewrite the first string to the first column:
Then rewrite the second string in the second column: 
And finally, rewrite the third string in the third column:
Ready. Roughly speaking, transpose - it means to turn the matrix of the side.
4) fourth action. Amount (difference) matrices.
The amount of matrices Action is simple.
Not all matrices can be folded. To perform the addition of (subtracting) matrices, it is necessary that they are the same in size.
For example, if the "two to two" matrix is \u200b\u200bgiven, then it can only be folded with the "two two" matrix and no other! 
Example:
Fold the matrices 
and 
In order to fold the matrices, it is necessary to fold their corresponding elements.:
For the difference of matrices, the rule is similar it is necessary to find the difference between the corresponding elements..
Example:
Find the difference Matrix 
, 
And how to solve this example is easier to not get confused? It is advisable to get rid of extra minuses, for this we will make a minus in the matrix:
Note: In the theory of higher mathematics, the school concept "subtraction" is not. Instead of the phrase "of this, it is always possible to say" to this add a negative number. " That is, subtraction is a special case of addition.
5) Fifth action. Matrix multiplication.
What matrices can be multiplied?
To make the matrix you can multiply on the matrix you need, so that the number of the matrix columns is equal to the number of matrix strings.
Example:
Is it possible to multiply the matrix on the matrix?
So, multiplying the data of the matrix can be.
But if the matrices rearrange in places, then, in this case, the multiplication is no longer possible!
Therefore, it is impossible to perform multiplication:
Not so rarely, tasks are encountered when the student is proposed to multiply the matrix, whose multiplication is obviously impossible.
It should be noted that in some cases you can multiply the matrix and so, and so.
For example, for matrices, and possibly multiplication and multiplication
In order to produce multiplication of the matrix A to an arbitrary number α, you need the elements of the matrix A. Multiply to the number α, i.e. The work of the matrix to the number will be as follows:
Example 1. Find a matrix 3. A.for the matrix
Decision. In accordance with the definition of multiplying the elements of the matrix A. 3 and get
It was a completely simple example of multiplying the matrix by a number with integers. There are also simple examples ahead, but already, where among multipliers and elements of matrices - fractions, variables (letter notation), because the laws of multiplication act not only for integer numbers, so it is never harmful to repeat them.
Example 2. A. by number α if 
,
.
A. On α, not forgetting that with multiplication of fractions, the numerator of the first fraction is multiplied by the number of the first fraction and the product is written to the numerator, and the denominator of the first fraction is multiplied by the channel of the second fraction and the product is written to the denominator. Upon receipt of the second element of the first line of a new matrix, the resulting fraction was reduced by 2, it must be done. Receive
Example 3. Perform the multiplication of the matrix A. by number α if
,
.
Decision. Multiply elements of the matrix A. On α, not being destroyed in the letter notation, without forgetting to leave a minus before the second element of the second line of the new matrix, and remember that the result of multiplying the number to the number to it is there is a unit (the first element of the third line). Receive
.
Example 4. Perform the multiplication of the matrix A. by number α if 
,
.
Decision. We remember that with multiplication of the number to the degree to the number to the degree indicators add up. Receive
.
This example, among other things, clearly demonstrates that the actions of multiplication of the matrix to a number can be read (and recorded) in the reverse order and is called it by the submissance of a constant factor in front of the matrix.
In combination of S. addition and subtraction of matrices The multiplication operation of the matrix to the number can form various matrix expressions, for example, 5 A. − 3B. , 4A. + 2B. .
The multiplication properties of the matrix
(here a, b - matrices, - numbers, 1 - number one)
1. 
2. 
3. 
Properties (1) and (2) bind multiplication of the matrix by a number with the addition of matrices. There is also a very important link between the multiplication of the matrix to the number and multiplying the matrices themselves:
i.e. if in the work of the matrices one of the multipliers is multiplied by the number, then all the work will multiply by the number.
Multiplication of the matrix to the number - This is an operation on the matrix, as a result of which each element is multiplied by a valuable or complex number. It looks mathematical language it is:
$$ b \u003d \\ lambda \\ cdot a \\ rightarrow b_ (ij) \u003d \\ lambda a_ (ij) $$
It is worth noting that the resulting matrix $ b $ as a result should be obtained by the same dimension that the initial matrix $ a $ has possessed. You can also pay attention to such a fact: $ \\ lambda \\ cdot a \u003d a \\ cdot \\ lambda $, that is, it is possible to change places multipliers and this work will not change.
It will be useful to use the operation of the multiplication of the matrix by the number when making a common factor beyond the matrix. In this case, each element of the matrix is \u200b\u200bdivided into the number of $ \\ lambda $, and it is removed in front of the matrix.
Properties
- Distributional law relative to matrices: $$ \\ lambda \\ cdot (a + b) \u003d \\ lambda a + \\ lambda b $$ multiplication of the amount of matrices to the number can be replaced by the amount of works of each individual matrix to this number
- Distributional law relative to real (integrated) numbers: $$ (\\ lambda + \\ mu) \\ Cdot a \u003d \\ lambda a + \\ mu a $$ Multiplication of the matrix in the amount of numbers can be replaced by the amount of works of each number on the matrix
- Associative law: $$ \\ lambda \\ cdot (\\ mu \\ cdot a) \u003d (\\ lambda \\ cdot \\ mu) a $$ It is convenient to use if you need to make a common multiplier from the matrix in front of it, with a domain already standing in front of it coefficient
- There is a special number $ \\ lambda \u003d 1 $, thanks to which the matrix remains unchanged $$ 1 \\ Cdot a \u003d a \\ cdot 1 \u003d a $$
- Multiplication of the matrix to zero leads to the fact that each element of the matrices is reset and the matrix becomes the zero of the same dimension, which was initially: $$ 0 \\ Cdot a \u003d 0 $$
Examples of solutions
| Example |
| It is given $ a \u003d \\ begin (Pmatrix) 2 & -1 & 4 \\\\ 0 & 9 & 3 \\\\ - 2 & -3 & 5 \\ END (PMATRIX) $ and the actual number $ \\ lambda \u003d $ 2. Multiply the number on the matrix. |
| Decision |
|
We write down the mathematical operation of multiplication and at the same time we remember the rule that reads: the matrix is \u200b\u200bmultiplied by the number element. $$ \\ lambda \\ cdot a \u003d 2 \\ CDOT \\ BEGIN (PMATRIX) 2 & -1 & 4 \\\\ 0 & 9 & 3 \\\\ - 2 & -3 & 5 \\ END (PMATRIX) \u003d \\ Begin (PMATRIX) 2 \\ CDOT 2 & 2 \\ CDOT (-1) & 2 \\ CDOT 4 \\\\ 2 \\ CDOT 0 & 2 \\ CDOT 9 & 2 \\ CDOT 3 \\\\ 2 \\ CDOT (-2) & 2 \\ CDOT (-3) & 2 \\ CDOT 5 \\ ED (PMATRIX) \u003d $$ $$ \u003d \\ BEGIN (PMATRIX) 4 & -2 & 8 \\\\ 0 & 18 & 6 \\\\ - 4 & -6 & 10 \\ End (PMATRIX) $$ As a result, we see that each number that standing in the matrix doubled towards the initial value. If it is impossible to solve your task, then send it to us. We will provide a detailed decision. You can familiarize yourself with the course of calculation and learn information. This will help in a timely manner at the teacher! |
| Answer |
| $$ \\ Lambda \\ Cdot A \u003d \\ BEGIN (PMATRIX) 4 & -2 & 8 \\\\ 0 & 18 & 6 \\\\ - 4 & -6 & 10 \\ End (PMATRIX) $$ |
