Topologie- ein ziemlich schönes, klangvolles Wort, das in manchen nicht-mathematischen Kreisen sehr beliebt war und mich schon in der 9. Klasse interessierte. Eine genaue Vorstellung hatte ich natürlich nicht, aber ich vermutete, dass alles mit der Geometrie zusammenhängt.
Die Worte und der Text wurden so ausgewählt, dass alles „intuitiv klar“ war. Das Ergebnis ist ein völliger Mangel an mathematischen Kenntnissen.
Was ist Topologie? ? Ich sage gleich, dass es mindestens zwei Begriffe „Topologie“ gibt – einer davon bezeichnet einfach eine bestimmte mathematische Struktur, der zweite trägt eine ganze Wissenschaft in sich. Diese Wissenschaft besteht darin, die Eigenschaften eines Objekts zu untersuchen, die sich nicht ändern, wenn es deformiert wird.
Anschauliches Beispiel 1. Bagelbecher.
Wir sehen, dass sich der Becher durch kontinuierliche Verformungen in einen Donut (umgangssprachlich einen „zweidimensionalen Torus“) verwandelt. Es wurde festgestellt, dass die Topologie untersucht, was bei solchen Verformungen unverändert bleibt. In diesem Fall bleibt die Anzahl der „Löcher“ im Objekt unverändert – es gibt nur eines. Im Moment lassen wir es so wie es ist, wir werden es etwas später herausfinden)
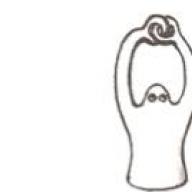
Anschauliches Beispiel 2. Topologischer Mensch.

Durch kontinuierliche Verformungen kann ein Mensch (siehe Bild) seine Finger entwirren – eine Tatsache. Es ist nicht sofort offensichtlich, aber Sie können es erraten. Aber wenn unser Topologe die Weitsicht hätte, eine Uhr auf einen Zeiger zu stellen, dann wäre unsere Aufgabe unmöglich.
Damit wir uns verstehen
Ich hoffe also, dass ein paar Beispiele etwas Klarheit darüber bringen, was passiert.Versuchen wir, das alles auf kindische Weise zu formalisieren.
Wir gehen davon aus, dass wir mit Plastilinfiguren arbeiten und Plastilin kann Dehnen, Komprimieren, Kleben verschiedener Punkte und Reißen sind verboten. Homöomorph sind Figuren, die durch kontinuierliche Verformungen, die etwas früher beschrieben wurden, ineinander übergehen.
Ein sehr nützlicher Koffer ist eine Kugel mit Griffen. Eine Kugel kann 0 Griffe haben – dann ist sie nur eine Kugel, vielleicht einer – dann ist sie ein Donut (im allgemeinen Sprachgebrauch ein „zweidimensionaler Torus“) usw.
Warum sticht eine Kugel mit Griffen unter anderen Figuren hervor? Alles ist ganz einfach – jede Figur ist homöomorph zu einer Kugel mit einer bestimmten Anzahl von Griffen. Das heißt, wir haben im Wesentlichen nichts anderes. O_o Jedes dreidimensionale Objekt ist wie eine Kugel mit einer bestimmten Anzahl von Griffen strukturiert. Sei es eine Tasse, ein Löffel, eine Gabel (Löffel=Gabel!), eine Computermaus, ein Mensch.
Dies ist ein ziemlich aussagekräftiger Satz, der bewiesen wurde. Nicht von uns und nicht jetzt. Genauer gesagt wurde es für eine viel allgemeinere Situation nachgewiesen. Lassen Sie es mich erklären: Wir haben uns darauf beschränkt, aus Plastilin geformte Figuren ohne Hohlräume in Betracht zu ziehen. Dies bringt folgende Probleme mit sich:
1) Wir können keine nicht orientierbare Oberfläche erhalten (Klein-Flasche, Möbius-Streifen, projektive Ebene),
2) wir beschränken uns auf zweidimensionale Oberflächen (n/a: Sphäre – zweidimensionale Oberfläche),
3) Wir können keine Flächen oder Figuren erhalten, die sich bis ins Unendliche erstrecken (natürlich können wir uns das vorstellen, aber keine Menge Plastilin wird ausreichen).
Der Möbius-Streifen

Klein-Flasche

Begriff Netzwerktopologie bezeichnet eine Möglichkeit, Computer in ein Netzwerk einzubinden. Möglicherweise hören Sie auch andere Namen - Netzwerkstruktur oder Netzwerkkonfiguration (Es ist das Gleiche). Darüber hinaus umfasst das Konzept der Topologie viele Regeln, die die Platzierung von Computern, Methoden zur Kabelverlegung, Methoden zur Platzierung von Anschlussgeräten und vieles mehr bestimmen. Bis heute wurden mehrere grundlegende Topologien gebildet und etabliert. Davon können wir feststellen: „ Reifen”, “Ring" Und " Stern”.
Bus-Topologie
Topologie Reifen (oder wie es oft genannt wird gemeinsamer Bus oder Autobahn ) beinhaltet die Verwendung eines Kabels, an das alle Workstations angeschlossen sind. Das gemeinsame Kabel wird abwechselnd von allen Stationen genutzt. Alle von einzelnen Workstations gesendeten Nachrichten werden von allen anderen mit dem Netzwerk verbundenen Computern empfangen und abgehört. Aus diesem Stream wählt jede Workstation Nachrichten aus, die nur an sie gerichtet sind.
Vorteile der Bustopologie:
- einfache Einrichtung;
- relativ einfache Installation und geringe Kosten, wenn sich alle Arbeitsplätze in der Nähe befinden;
- Der Ausfall eines oder mehrerer Arbeitsplätze hat keinerlei Auswirkungen auf den Betrieb des gesamten Netzwerks.
Nachteile der Bustopologie:
- Busprobleme irgendwo (Kabelbruch, Ausfall des Netzwerksteckers) führen zur Funktionsunfähigkeit des Netzwerks;
- Schwierigkeiten bei der Fehlerbehebung;
- Geringe Leistung – zu jedem Zeitpunkt kann nur ein Computer Daten an das Netzwerk übertragen; mit zunehmender Anzahl von Arbeitsplätzen nimmt die Netzwerkleistung ab;
- schlechte Skalierbarkeit – um neue Workstations hinzuzufügen, müssen Teile des vorhandenen Busses ersetzt werden.
Lokale Netzwerke wurden nach der „Bus“-Topologie aufgebaut Koaxialkabel. In diesem Fall fungierten durch T-Stecker verbundene Koaxialkabelabschnitte als Bus. Der Bus fuhr durch alle Räume und näherte sich jedem Computer. Der seitliche Stift des T-Steckers wurde in den Anschluss auf der Netzwerkkarte gesteckt. So sah es aus:  Mittlerweile sind solche Netzwerke hoffnungslos veraltet und wurden überall durch „Stern“-Twisted-Pair-Kabel ersetzt, aber in einigen Unternehmen ist immer noch Ausrüstung für Koaxialkabel zu sehen.
Mittlerweile sind solche Netzwerke hoffnungslos veraltet und wurden überall durch „Stern“-Twisted-Pair-Kabel ersetzt, aber in einigen Unternehmen ist immer noch Ausrüstung für Koaxialkabel zu sehen.
Ringtopologie
Ring ist eine lokale Netzwerktopologie, bei der Workstations in Reihe miteinander verbunden sind und einen geschlossenen Ring bilden. Die Datenübertragung von einem Arbeitsplatz zum anderen erfolgt in einer Richtung (im Kreis). Jeder PC fungiert als Repeater und leitet Nachrichten an den nächsten PC weiter, d. h. Daten werden wie bei einem Staffellauf von einem Computer zum anderen übertragen. Empfängt ein Computer Daten, die für einen anderen Computer bestimmt sind, überträgt er diese im Ring weiter, andernfalls werden sie nicht weiter übertragen.
Vorteile der Ringtopologie:
- erleichterte Installation;
- fast vollständiges Fehlen zusätzlicher Ausrüstung;
- Möglichkeit eines stabilen Betriebs ohne nennenswerten Einbruch der Datenübertragungsgeschwindigkeit bei starker Netzwerklast.
Allerdings hat der „Ring“ auch erhebliche Nachteile:
- jeder Arbeitsplatz muss sich aktiv an der Informationsübertragung beteiligen; Fällt mindestens einer von ihnen aus oder reißt das Kabel, stoppt der Betrieb des gesamten Netzwerks;
- der Anschluss eines neuen Arbeitsplatzes erfordert eine kurzfristige Abschaltung des Netzwerks, da der Ring während der Installation eines neuen PCs geöffnet sein muss;
- Komplexität der Konfiguration und Einrichtung;
- Schwierigkeiten bei der Fehlerbehebung.
Die Ringnetzwerktopologie wird recht selten verwendet. Seine Hauptanwendung fand es in Glasfasernetze Token-Ring-Standard.
Sterntopologie
Stern ist eine lokale Netzwerktopologie, bei der jede Workstation mit einem zentralen Gerät (Switch oder Router) verbunden ist. Das zentrale Gerät steuert die Bewegung von Paketen im Netzwerk. Jeder Computer ist über eine Netzwerkkarte mit einem separaten Kabel mit dem Switch verbunden. Bei Bedarf können Sie mehrere Netzwerke zu einer Sterntopologie zusammenfassen – als Ergebnis erhalten Sie eine Netzwerkkonfiguration mit baumartig Topologie. Baumtopologie ist in großen Unternehmen üblich. Wir werden in diesem Artikel nicht näher darauf eingehen.
Die „Stern“-Topologie ist heute die wichtigste beim Aufbau lokaler Netzwerke. Dies geschah aufgrund seiner vielen Vorteile:
- Der Ausfall eines Arbeitsplatzrechners oder eine Beschädigung seines Kabels beeinträchtigt nicht den Betrieb des gesamten Netzwerks;
- hervorragende Skalierbarkeit: Um eine neue Workstation anzuschließen, verlegen Sie einfach ein separates Kabel vom Switch;
- einfache Fehlerbehebung und Netzwerkunterbrechungen;
- Hochleistung;
- einfache Einrichtung und Verwaltung;
- Zusätzliche Geräte können problemlos in das Netzwerk integriert werden.
Allerdings ist der „Stern“ wie jede Topologie nicht ohne Nachteile:
- Ein Ausfall des zentralen Switches führt zur Funktionsunfähigkeit des gesamten Netzwerks;
- zusätzliche Kosten für Netzwerkgeräte – ein Gerät, an das alle Computer im Netzwerk angeschlossen werden (Switch);
- Die Anzahl der Arbeitsplätze ist durch die Anzahl der Ports im zentralen Switch begrenzt.
Stern – die gebräuchlichste Topologie für kabelgebundene und kabellose Netzwerke. Ein Beispiel für eine Sterntopologie ist ein Netzwerk mit einem Twisted-Pair-Kabel und einem Switch als zentralem Gerät. Dies sind die Netzwerke, die in den meisten Organisationen zu finden sind.
Verwandt.
Inhalt
Allgemeine Topologie
Einheitliche Topologie
Algebraische Topologie
Stückweise lineare Topologie
Topologie von Mannigfaltigkeiten
Hauptphasen der Topologieentwicklung
1. Allgemeine Topologie
Der Teil der Theorie, der auf das axiomatische Studium der Kontinuität ausgerichtet ist, wird als Allgemeine Theorie bezeichnet. Die Allgemeine Theorie bildet neben der Algebra die Grundlage der modernen mengentheoretischen Methode in der Mathematik.
Axiomatisch kann Kontinuität auf viele (im Allgemeinen ungleiche) Arten definiert werden. Eine allgemein anerkannte Axiomatik basiert auf dem Konzept einer offenen Menge. Eine topologische Struktur oder Topologie auf einer Menge X ist eine Familie ihrer Teilmengen, sogenannte offene Mengen, so dass:
1) die leere Menge ∅ und alle X sind offen;
2) Die Vereinigung einer beliebigen Zahl und der Durchschnitt einer endlichen Anzahl offener Mengen ist offen.
Eine Menge, auf der eine topologische Struktur gegeben ist, wird topologischer Raum genannt. Im topologischen Raum X kann man alle Grundkonzepte der Elementaranalysis im Zusammenhang mit der Kontinuität definieren. Zum Beispiel eine Umgebung von Punkt x
∈ X ist eine beliebige offene Menge, die diesen Punkt enthält; Eine Menge A⊂X heißt abgeschlossen, wenn ihr Komplement XA offen ist; der Abschluss einer Menge A ist die kleinste abgeschlossene Menge, die A enthält; Wenn dieser Abschluss mit X zusammenfällt, heißt A überall in X dicht usw.
Per Definition sind ∅ und X sowohl geschlossene als auch offene Mengen. Wenn es in X keine anderen Mengen gibt, die sowohl geschlossen als auch offen sind, dann heißt der topologische Raum X zusammenhängend. Ein visuell verbundener Raum besteht aus einem „Stück“, während ein inkohärenter Raum aus mehreren besteht.
Jede Teilmenge A eines topologischen Raums X hat eine natürliche topologische Struktur, die aus Schnittpunkten mit A offener Mengen aus Seien Sie Mengen, die zusammen mit einem beliebigen Punkt einige seiner ε-Umgebung enthalten (eine Kugel mit dem Radius ε, die an diesem Punkt zentriert ist). Insbesondere ist jede Teilmenge des n-dimensionalen euklidischen Raums |R n ein topologischer Raum. Die Theorie solcher Räume (unter dem Namen „geometrische Theorie“) und die Theorie metrischer Räume gehören traditionell zur allgemeinen Theorie.
Die geometrische Theorie gliedert sich ganz klar in zwei Teile: das Studium von Teilmengen |R n beliebiger Komplexität, vorbehaltlich bestimmter allgemeiner Einschränkungen (ein Beispiel ist die sogenannte Theorie der Kontinua, also verbundener begrenzter geschlossener Mengen) und das Studium der Möglichkeiten, wie |R n einfache topologische Räume wie Kugel, Ball usw. eingebettet werden können. (Einbettungen in |R n , beispielsweise Kugeln, können sehr komplex sein).
Eine offene Überdeckung eines topologischen Raums X ist eine Familie seiner offenen Mengen, deren Vereinigung das Ganze von X ist. Ein topologischer Raum aus Elementen, die die Abdeckung bilden. Der klassische Satz von Heine-Borel besagt, dass jede begrenzte abgeschlossene Teilmenge |R n kompakt ist. Es stellt sich heraus, dass alle Grundsätze der Elementaranalysis über begrenzte abgeschlossene Mengen (z. B. der Satz von Weierstrass, dass auf einer solchen Menge eine stetige Funktion ihren größten Wert erreicht) für alle kompakten topologischen Räume gelten. Dies bestimmt die grundlegende Rolle, die kompakte Räume in der modernen Mathematik spielen (insbesondere im Zusammenhang mit Existenzsätzen). Die Identifizierung der Klasse kompakter topologischer Räume war eine der größten Errungenschaften der Allgemeinen Theorie und hatte allgemeine mathematische Bedeutung.
Eine offene Abdeckung (V β) heißt in einer Abdeckung (U α) eingeschrieben, wenn es für jedes β ein α gibt, so dass V β ⊂ U α. Eine Überdeckung (V β) heißt lokal endlich, wenn jeder Punkt x ∈ X eine Umgebung hat, die sich nur mit einer endlichen Anzahl von Elementen dieser Überdeckung schneidet.
Ein topologischer Raum heißt parakompakt, wenn jede offene Überdeckung eine lokal endliche Überdeckung enthalten kann. Die Klasse der parakompakten Räume ist ein Beispiel für Klassen topologischer Räume, die durch Auferlegen sogenannter Kompaktheitstypbedingungen erhalten werden. Diese Klasse ist sehr umfangreich, insbesondere enthält sie alle metrisierbaren topologischen Räume, also Räume X, in denen eine solche Metrik eingeführt werden kann
ρ, dass das von ρ in X erzeugte T. mit dem in X definierten T. übereinstimmt.
Die Multiplizität einer offenen Überdeckung ist die größte Zahl k, so dass es k ihrer Elemente gibt, die einen nichtleeren Durchschnitt haben. Die kleinste Zahl n mit der Eigenschaft, dass jede endliche offene Abdeckung eines topologischen Raums X eine offene Abdeckung der Multiplizität ≤n + 1 enthalten kann, wird mit dimX bezeichnet und als Dimension von X bezeichnet.
Diese Bezeichnung wird durch die Tatsache gerechtfertigt, dass dimX in elementaren geometrischen Situationen mit der üblicherweise verstandenen Dimension übereinstimmt, beispielsweise dim|R n = n. Es sind auch andere numerische Funktionen des topologischen Raums X möglich, die sich von dimX unterscheiden, aber im einfachsten Fall mit dimX zusammenfallen. Ihre Untersuchung ist Gegenstand der Allgemeinen Dimensionstheorie – des am stärksten geometrisch orientierten Teils des Allgemeinen T. Nur im Rahmen dieser Theorie ist es beispielsweise möglich, eine klare und ziemlich allgemeine Definition des intuitiven Konzepts von a zu geben geometrische Figur und insbesondere der Begriff einer Linie, Fläche usw.
Wichtige Klassen topologischer Räume erhält man durch die Einführung der sogenannten Trennungsaxiome. Ein Beispiel ist das sogenannte Hausdorff-Axiom oder T 2 -Axiom, das erfordert, dass zwei beliebige unterschiedliche Punkte disjunkte Nachbarschaften haben. Ein topologischer Raum, der dieses Axiom erfüllt, wird Hausdorff oder separierbar genannt. In der mathematischen Praxis sind seit einiger Zeit fast ausschließlich Hausdorff-Räume anzutreffen (z. B. ist jeder metrische Raum Hausdorff-Raum). Die Rolle topologischer Nicht-Hausdorff-Räume in Analysis und Geometrie nimmt jedoch ständig zu.
Topologische Räume, die Teilräume von Hausdorff(bi)kompakten Räumen sind, werden vollständig regulär oder Tichonow genannt. Sie können auch durch ein Axiom der Trennbarkeit charakterisiert werden, nämlich: ein Axiom, das dies für jeden Punkt x 0 erfordert
∈ X und jede abgeschlossene Menge F X, die es nicht enthält, existierte eine stetige Funktion g:
Topologische Räume, die offene Unterräume von Hausdorff-kompakten Räumen sind, werden lokal kompakte Räume genannt. Sie zeichnen sich (in der Klasse der Hausdorff-Räume) dadurch aus, dass jeder ihrer Punkte eine Umgebung mit kompaktem Abschluss hat (Beispiel: Euklidischer Raum). Jeder solche Raum wird durch einen Punkt zu einem kompakten ergänzt (Beispiel: Durch Addition eines Punktes aus der Ebene erhält man eine Kugel einer komplexen Variablen und aus |R n eine Kugel S n).
Eine Abbildung f:X → Y eines topologischen Raums wenn es eineindeutig ist und die inverse Abbildung f − 1:Y
→ X ist stetig. Eine solche Abbildung stellt eine Eins-zu-eins-Entsprechung zwischen offenen Mengen topologischer Räume X und Y her, die mit den Operationen Vereinigung und Schnittmenge von Mengen permutierbar ist. Daher sind alle topologischen Eigenschaften (d. h. Eigenschaften, die als offene Mengen formuliert sind) dieser Räume gleich, und aus topologischer Sicht sind homöomorphe topologische Räume (d. h. Räume, für die es mindestens einen Homöomorphismus X → gibt). J)
als identisch gelten (so wie in der euklidischen Geometrie Figuren, die durch Bewegung kombiniert werden können, als identisch gelten). Beispielsweise sind Kreis und Rand eines Quadrats, Sechsecks usw. homöomorph („topologisch identisch“). Im Allgemeinen sind zwei beliebige einfache (ohne Doppelpunkte) geschlossene Geraden homöomorph. Im Gegenteil, ein Kreis ist nicht homöomorph zu einer geraden Linie (weil das Entfernen eines Punktes nicht den Zusammenhang des Kreises verletzt, wohl aber den Zusammenhang der geraden Linie; aus dem gleichen Grund ist eine gerade Linie nicht homöomorph zu a Ebene, und ein Kreis ist nicht homöomorph zu einer Acht).
Ein Kreis ist auch nicht homöomorph zu einer Ebene (wirf nicht einen, sondern zwei Punkte weg).
Sei (X α) eine beliebige Familie topologischer Räume. Betrachten Sie die Menge X aller Familien der Form (x α ), wobei x α ∈ X α (das direkte Produkt der Mengen X α). Für jedes α definiert die Formel p α ((x α )) = x α eine Abbildung p α: X → X α (sogenannte Projektion). Im Allgemeinen kann man in X viele topologische Strukturen einführen, bezüglich derer alle Abbildungen p α stetig sind.
Unter diesen Strukturen gibt es die kleinste (die in jeder solchen Struktur enthalten ist). Die mit dieser topologischen Struktur ausgestattete Menge X heißt topologisches Produkt der topologischen Räume X α und wird mit dem Symbol ΠX α (und im Fall einer endlichen Anzahl von Faktoren mit dem Symbol ). Explizit können offene Mengen des Raums X als Vereinigungen endlicher Durchschnitte aller Mengen der Form p α −1 (U α) beschrieben werden, wobei U α offen in X α ist.
Der topologische Raum ∘ƒ=ƒ α für alle α. Der Raum |R n ist das topologische Produkt von n Instanzen der Zahlenlinie. Einer der wichtigsten Sätze der Allgemeinen Theorie ist die Aussage, dass das topologische Produkt kompakter topologischer Räume kompakt ist.
Wenn X ein topologischer Raum und Y eine beliebige Menge ist und eine Abbildung p: ist eine natürliche Projektion, die jedem Element x ∈ X seine Äquivalenzklasse zuordnet),
dann können wir die Frage aufwerfen, eine topologische Struktur in Y einzuführen, bezüglich derer die Abbildung p stetig ist. Die „reichste“ (an offenen Mengen) Struktur erhält man, wenn man alle Mengen V als offene Mengen in Y betrachtet
⊂ Y, für die die Menge f ‑1 (V) ⊂ Es hat die Eigenschaft, dass eine beliebige Abbildung ƒ : Y
→ Z ist genau dann stetig, wenn die Abbildung ƒ∘p: X → Z stetig ist. Eine stetige Abbildung p: X. Die kontinuierliche Abbildung p: X
→ Y heißt offen, wenn für jede offene Menge U ⊂ X die Menge p(U) in Y offen ist, und geschlossen, wenn für jede abgeschlossene Menge F ⊂ Karten ƒ : X
→ Y, für die ƒ(X) = Y, sind faktoriell.
Sei X ein topologischer Raum, A sein Unterraum und ƒ : A → Y eine kontinuierliche Abbildung. Unter der Annahme, dass die topologischen Räume X und Y disjunkt sind, führen wir X in ihre Vereinigung ein
∪ Y topologische Struktur, wobei die Vereinigungen offener Mengen aus X und Y als offene Mengen betrachtet werden. Im Raum X ∪ Y führen wir die kleinste Äquivalenzbeziehung ein, in der a ∼ ƒ(α) für jeden Punkt a
∈ A. Der entsprechende Quotientenraum wird mit X ∪ f Y bezeichnet und soll durch Kleben eines topologischen Raums X an einen topologischen Raum Y entlang A über eine kontinuierliche Karte ƒ erhalten werden. Dieser einfache und intuitive Vorgang erweist sich als sehr wichtig, da er es ermöglicht, aus relativ einfachen topologischen Räumen komplexere Werte zu erhalten. Wenn Y aus einem Punkt besteht, dann ist der Raum X
∪ f Y wird durch das Symbol X/A bezeichnet und soll aus X durch Kontraktion von A auf einen Punkt erhalten werden. Wenn beispielsweise X eine Scheibe und A ihr Grenzkreis ist, dann ist X/A homöomorph zu einer Kugel.
2. Einheitliche Topologie
Der Teil der Theorie, der sich mit dem axiomatischen Konzept der Kontinuität befasst, wird als einheitliche Theorie bezeichnet. Die aus der Analysis bekannte Definition der gleichmäßigen Stetigkeit numerischer Funktionen wird direkt auf Abbildungen beliebiger metrischer Räume übertragen. Daher wird die Axiomatik der gleichmäßigen Kontinuität normalerweise ausgehend von metrischen Räumen erhalten. Es werden zwei axiomatische Ansätze zur gleichmäßigen Kontinuität untersucht, die jeweils auf den Konzepten der Nähe und der diagonalen Einkreisung basieren.
Teilmengen A und B eines metrischen Raums die folgende Definition: (separierbare) Strukturnähe auf einer Menge X ist eine Beziehung δ auf der Menge aller ihrer Teilmengen, so dass:
1) ∅δ̅X (das Symbol δ̅ bezeichnet die Negation der Beziehung δ;
2)
Aδ̅B 1 und Aδ̅B 2 ⇔ Aδ(B 1 U B 2);
3) (x) δ̅ (y) ⇔ x ≠ y;
4) Wenn AδB, dann gibt es eine Menge Cδ̅B mit Aδ(XC).
Die Menge, in der die Proximity-Struktur angegeben ist, wird Proximity-Raum genannt. Eine Abbildung von einem Proximitätsraum X auf einen Proximitätsraum Y heißt nahe stetig, wenn die Bilder von Mengen, die in eine eins-zu-eins enge kontinuierliche Zuordnung
X → Y, dessen Umkehrung ebenfalls nahezu stetig ist (eine solche nahe stetige Abbildung wird als Äquimorphismus bezeichnet). In der einheitlichen Theorie werden äquimorphe Proximitätsräume als identisch betrachtet. Wie metrische Räume kann jeder Proximitätsraum durch Berücksichtigung einer Teilmenge in einen (Hausdorff-)topologischen Raum umgewandelt werden
U⊂X ist offen, wenn (x)δ̅(XU) für jeden Punkt x∈U. In diesem Fall erweisen sich benachbarte kontinuierliche Abbildungen als kontinuierliche Abbildungen. Die auf die beschriebene Weise aus Proximity-Räumen gewonnene Klasse topologischer Räume fällt mit der Klasse völlig regulärer topologischer Räume zusammen. Für jeden vollständig regulären Raum X stehen alle Proximity-Strukturen auf ein überall dichter Raum.
Die der Erweiterung bX entsprechende Proximity-Struktur δ ist dadurch gekennzeichnet, dass AδB genau dann gilt, wenn sich die Abschlüsse der Mengen A und B in bX schneiden. Insbesondere gibt es auf jedem kompakten topologischen Hausdorff-Raum X eine einzigartige Proximity-Struktur, die seine topologische Struktur erzeugt.
Ein anderer Ansatz basiert auf der Tatsache, dass die gleichmäßige Kontinuität in einem metrischen Raum X durch die Beziehung „Punkte x und y haben einen Abstand von nicht mehr als ε“ definiert werden kann. Allgemein betrachtet ist eine Relation auf X nichts anderes als eine beliebige Teilmenge U des direkten Produkts XХX. Die Relation „Identität“ ist aus dieser Sicht eine Diagonale Δ ⊂ X × X, also eine Menge von Punkten der Form (x, x), x∈X. Für jede Beziehung U ist die Umkehrbeziehung U −1 = ((x,y); (y,x) definiert
∈ U) und für zwei beliebige Beziehungen U und V ist ihre Zusammensetzung definiert U · V = ((x,y); es existiert z ∈ X mit (x, z) ∈ U, (z,y) ∈ V ). Eine Familie von Beziehungen (U) heißt eine (separierbare) einheitliche Struktur auf X (und Beziehungen U werden diagonale Umgebungen genannt), wenn: 1) der Schnittpunkt zweier diagonaler Umgebungen eine diagonale Umgebung enthält; 2) Jede diagonale Umgebung enthält
Δ, und der Schnittpunkt aller diagonalen Umgebungen fällt mit Δ zusammen; 3) zusammen mit U ist die Umgebung der Diagonale auch U −1 ; 4) Für jede Umgebung der Diagonale U gibt es eine Umgebung der Diagonale W mit W o W
⊂ U. Eine Menge mit einer einheitlichen Struktur wird als einheitlicher Raum bezeichnet. Eine Abbildung ƒ : X → Y eines einheitlichen Raums
Х ƒ : X Х X → Y Х Y einer beliebigen Umgebung einer Diagonale V ⊂ Y Х Y enthält eine Umgebung einer Diagonale von gleichmäßig stetige Abbildung X
→ Y, deren Umkehrung ebenfalls eine gleichmäßig stetige Abbildung ist.
Im einheitlichen T. gelten solche einheitlichen Räume als identisch. Jede einheitliche Struktur auf
In diesem Fall erweisen sich gleichmäßig kontinuierliche Karten als nahezu kontinuierlich.
3. Algebraische Topologie
Jeder topologische Raum ( X)
→ h(Y) (oder h(f) : h(Y) → h(X), was der Identitätshomomorphismus ist, wenn ƒ die Identitätskarte ist. Wenn h(f 1 ○ f 2) = h(f 1)
○ h(f 2) (bzw. h(f 1 ○ f 2) = h(f 2) ○ h(f 1), dann heißt h ein Funktor (bzw. ein Kofunktor). Die meisten algebraischen T Probleme. hängt irgendwie mit dem Ausbreitungsproblem zusammen: für eine gegebene kontinuierliche Abbildung f: A
→ Y eines Unterraums A ⊂ X in einen topologischen Raum Y, finden Sie eine kontinuierliche Abbildung g:
→ X – Einbettungskarte (i(a) = a für jeden Punkt a ∈ A). Wenn eine solche kontinuierliche Abbildung g existiert, dann gibt es für jeden Funktor (Kofunktor) h einen Homomorphismus (φ: h(X)
→ h(Y) (Homomorphismus φ: h(Y) → h(X)), so dass h(f) = φ ○ h(i) (bzw. h(f) = h(i) ○ φ); es wird der Homomorphismus φ = h(g) sein. Daher die Nichtexistenz eines Homomorphismus
φ (für mindestens einen Funktor h) impliziert die Nichtexistenz der Abbildung g. Fast alle Methoden des algebraischen T lassen sich tatsächlich auf dieses einfache Prinzip reduzieren. Beispielsweise gibt es einen Funktor h, dessen Wert auf der Kugel E n eine triviale Gruppe ist und auf der die Kugel begrenzenden Kugel S n-1 ist eine nicht triviale Gruppe. Dies impliziert bereits das Fehlen der sogenannten Retraktion – einer kontinuierlichen Abbildung p:E n
→ S n-1 , fixiert auf S n-1 , das heißt, so dass die Zusammensetzung p·i, wobei i: S n‑1 → E n eine Einbettungskarte ist, eine Identitätskarte ist (wenn p existiert, dann die Identitätskarte der Gruppe h(S n-1) wird eine Zusammensetzung von Abbildungen h(i) : h(S n-1) sein
→ h(E n) und h(p) : h(E n) → h(S n-1), was für die triviale Gruppe h(E n) unmöglich ist. Dieser im Wesentlichen elementare geometrische und (für n = 2) visuell offensichtliche Sachverhalt (physikalisch gemeint ist die Möglichkeit, eine Trommel auf einen runden Reifen zu spannen) konnte jedoch ohne den Einsatz algebraisch-topologischer Methoden bisher nicht nachgewiesen werden. Seine unmittelbare Konsequenz ist die Aussage, dass jede kontinuierliche Karte ƒ : E n
→ E n hat mindestens einen Fixpunkt, das heißt, die Gleichung ƒ(x) = x hat mindestens eine Lösung in E n (wenn ƒ(x) ≠ x für alle x ∈ E n , dann gilt p(x ) ein Punkt von S n-1 kollinear zu den Punkten ƒ(x) und x und so, dass das Segment mit den Enden ƒ(x) und p(x) x enthält, erhalten wir die Retraktion p: E n
→ S n-1). Dieser Fixpunktsatz war einer der ersten Sätze der algebraischen Theorie und wurde dann zur Quelle einer ganzen Reihe verschiedener Sätze über die Existenz von Lösungen von Gleichungen.
Im Allgemeinen gilt: Je komplexer die algebraische Struktur von Objekten h(X) ist, desto einfacher ist es, die Nichtexistenz eines Homomorphismus (φ) festzustellen. Daher berücksichtigen algebraische Theorien algebraische Objekte äußerst komplexer Natur und deren Anforderungen Die Entwicklung der algebraischen Topologie hat die Entwicklung der abstrakten Algebra maßgeblich vorangetrieben.
Ein topologischer Raum
⊂ X n-1 ⊂ X n ⊂... (genannt die Skelette des Zellraums X), deren Vereinigung das Ganze von X genau dann, wenn für jedes n die Menge U gilt
∩ X n ist offen in X n ; 2) X n wird aus 3) X 0 besteht aus isolierten Punkten. Somit besteht die Struktur eines Zellraums grob gesagt darin, dass er als Vereinigung von Mengen dargestellt wird, die homöomorph zu offenen Kugeln sind (diese Mengen werden Zellen genannt). In algebraischen Techniken werden fast ausschließlich Zellräume untersucht, da die Spezifität der Probleme algebraischer Techniken für sie bereits vollständig zum Ausdruck kommt. Darüber hinaus sind tatsächlich einige besonders einfache Zellräume (wie Polyeder, siehe unten) für algebraische Systeme von Interesse, aber die Eingrenzung der Klasse der Zellräume erschwert in der Regel die Untersuchung erheblich (da viele nützliche Operationen an Zellräumen der Fall sind). abgeleitet von der Klasse der Polyeder).
Zwei stetige Abbildungen f, g: f 0 = ƒ und f 1 = g (kontinuierliche Abhängigkeit von t bedeutet, dass die Formel F(x, t) = f t (x), x ∈ X, t
∈ definiert eine kontinuierliche Abbildung F: X Х → Y; Diese Abbildung sowie die Familie (f t ) werden als Homotopie bezeichnet, die ƒ mit g verbindet. Die Menge aller kontinuierlichen Abbildungen
X → Y zerfällt in Homotopieklassen von zueinander homotopen Abbildungen. Die Menge der Homotopieklassen stetiger Abbildungen von X nach Y wird mit dem Symbol bezeichnet. Die Untersuchung der Eigenschaften von Homotopiebeziehungen und insbesondere von Mengen ist Gegenstand der sogenannten Homotopietopologie (oder Homotopietheorie). Für die meisten interessanten topologischen Räume sind die Mengen endlich oder abzählbar und können explizit effizient berechnet werden. Topologische Räume
X → Y und g: Y → X, so dass die kontinuierlichen Abbildungen g·f: X → X und f·g: Y → Y homotopisch zu den entsprechenden Identitätskarten sind. In der Homotopietheorie sollten solche Räume als identisch betrachtet werden (alle ihre „Homotopieinvarianten“ fallen zusammen).
Es zeigt sich, dass in vielen Fällen (insbesondere für Zellräume) die Lösbarkeit des Ausbreitungsproblems nur von der Homotopieklasse der kontinuierlichen Karte ƒ : A → Y abhängt; Genauer gesagt, wenn für ƒ die Ausbreitung g: X
→ Y existiert, dann gibt es für jede Homotopie f t: A → Y (mit f 0 = f) eine Verteilung g t: X → Y mit g 0 = g. Daher können wir anstelle von ƒ seine Homotopieklasse [f] betrachten und dementsprechend nur homotopieinvariante Funktoren (Kofunktoren) h untersuchen, d. h. solche mit h(f 0) = h(f 1), wenn die Karten f 0 und f 1 homotopisch. Dies führt zu einer so engen Verflechtung von Algebra- und Homotopietheorie, dass sie als eine einzige Disziplin betrachtet werden können.
Für jeden topologischen Raum Y definieren die Formeln h(X) = und h(f) = [φ○f], wobei f: X 1 → X 2 und φ : X 2 → Y, einen homotopieinvarianten Kofunktor h, nämlich Es wird gesagt, dass es durch den topologischen Raum Y dargestellt wird. Dies ist eine Standardmethode (und im Wesentlichen die einzige) zur Konstruktion homotopieinvarianter Kofunktoren. Damit sich herausstellt, dass die Menge h(X) beispielsweise eine Gruppe ist, muss Y entsprechend gewählt werden, um beispielsweise zu verlangen, dass es sich um eine topologische Gruppe handelt (im Allgemeinen ist dies nicht ganz richtig: es Es ist notwendig, einen Punkt x 0 in Darüber hinaus reicht es aus, wenn Y eine topologische Gruppe ist
„im Sinne der Homotopie“, das heißt, dass die Axiome der Assoziativität und der Existenz eines inversen Elements (die tatsächlich die Koinzidenz einiger Abbildungen behaupten) nur „bis zur Homotopie“ erfüllt wären. Solche topologischen Räume werden H-Räume genannt. Somit definiert jeder H-Raum Y einen homotopieinvarianten Kofunktor h(X) = , dessen Werte Gruppen sind.
Auf ähnliche („duale“) Weise wird jeder topologische Raum Y durch die Formeln h(X) = , h(f) = [ƒ ○φ] definiert, wobei ƒ : X 1
→ X 2 und φ : Y → X 1 , ein Funktor h. Damit h(X) eine Gruppe ist, muss Y eine bestimmte algebraische Struktur haben, die in einem wohldefinierten Sinne dual zur Struktur des H-Raums ist. Mit dieser Struktur ausgestattete topologische Räume werden Co-N-Räume genannt. Ein Beispiel für einen Co-H-Raum ist die n-dimensionale Kugel S n (für n ≥ 1).
Somit definiert für jeden topologischen Raum X die Formel π n X = eine bestimmte Gruppe π n X, n ≥ 1, die als n-te Homotopiegruppe des Raums Für n > 1 Gruppe
π n X ist kommutativ. Wenn π 1 X = (1), dann heißt X einfach zusammenhängend.
Ein Zellraum X heißt Raum K(G, n), wenn π i (X) = 0 für i ≠ n und π n X = G; Ein solcher Zellraum existiert für jedes n ≥ 1 und jede Gruppe G (kommutativ für n > 1) und ist bis zur Homotopieäquivalenz eindeutig bestimmt.
Für n > 1 (und auch für n = 1, wenn die Gruppe G kommutativ ist) erweist sich der Raum K(G, n) als H-Raum und stellt daher eine bestimmte Gruppe H n (X; G) = dar . Diese Gruppe wird als n-dimensionale Kohomologiegruppe eines topologischen Raums X mit der Koeffizientengruppe G bezeichnet. Sie ist ein typischer Vertreter einer Reihe wichtiger Kofunktoren, darunter beispielsweise der K-Funktor KO(X) = , dargestellt durch das sogenannte unendlichdimensionale Grassmannsche BO, eine Gruppe orientierter Kobordismen
Ω n X usw.
Wenn G ein Ring ist, dann ist die direkte Summe H*(X; G) der Gruppen H n (X; G) eine Algebra über G. Darüber hinaus hat diese direkte Summe eine sehr komplexe algebraische Struktur, in der (für G = Z p, wobei Z p eine zyklische Gruppe der Ordnung p ist) beinhaltet die Wirkung einer nichtkommutativen Algebra p, der sogenannten Steenrod-Algebra, auf H*(X; G). Die Komplexität dieser Struktur ermöglicht einerseits die Entwicklung effektiver (aber keineswegs einfacher) Methoden zur Berechnung von Gruppen H n (X; G) und andererseits die Herstellung von Verbindungen zwischen Gruppen H n (X ; G) und andere homotopieinvariante Funktoren (z. B. Homotopiegruppen π n X),
die es oft ermöglichen, diese Funktoren explizit zu berechnen.
Historisch gesehen gingen den Kohomologiegruppen die sogenannten Homotopiegruppen H n (X; G) voraus, bei denen es sich um Homotopiegruppen π n M(X, G) eines Zellraums M(X, G) handelt, die eindeutig aus dem Zellraum konstruiert wurden X und die Gruppe G. Homologiegruppen und Kohomologie sind in gewissem Sinne dual zueinander und ihre Theorien sind im Wesentlichen äquivalent. Die algebraische Struktur von Homologiegruppen ist jedoch weniger bekannt (diese Gruppen stellen beispielsweise keine Algebra, sondern eine sogenannte Kohlegebra dar), weshalb in Berechnungen üblicherweise Kohomologiegruppen verwendet werden. Gleichzeitig erweisen sich Homologiegruppen in manchen Fragestellungen als praktischer und werden daher auch untersucht. Der Teil der algebraischen Theorie, der sich mit der Untersuchung (und Anwendung) von Homologie- und Kohomologiegruppen befasst, wird Homologietheorie genannt.
Die Übertragung der Ergebnisse der algebraischen Theorie auf Räume, die allgemeiner als zelluläre Räume sind, ist Gegenstand der sogenannten allgemeinen algebraischen Theorie. Insbesondere untersucht die allgemeine Homologietheorie die Homologie- und Kohomologiegruppen beliebiger topologischer Räume und ihre Anwendungen. Es zeigt sich, dass außerhalb der Klasse der kompakten zellulären Räume unterschiedliche Ansätze zur Konstruktion dieser Gruppen im Allgemeinen zu unterschiedlichen Ergebnissen führen, so dass für nichtzelluläre topologische Räume eine ganze Reihe verschiedener Homologie- und Kohomologiegruppen entsteht. Die Hauptanwendung der allgemeinen Homologietheorie liegt in der Dimensionstheorie und in der Theorie der sogenannten Dualitätsgesetze (die die Beziehung zwischen den topologischen Eigenschaften zweier zusätzlicher Teilmengen des topologischen Raums beschreiben), und ihre Entwicklung wurde maßgeblich vorangetrieben durch die Bedürfnisse dieser Theorien.
4. Stückweise lineare Topologie
Eine Teilmenge P ∈ |R n heißt Kegel mit Scheitelpunkt a und Basis B, wenn jeder ihrer Punkte zu einem eindeutigen Segment der Form ab gehört, wobei b ∈ B. Eine Teilmenge X ∈ |R n heißt Polyeder, falls vorhanden seiner Punkte hat eine Umgebung in X, deren Abschluss ein Kegel mit kompakter Basis ist. Eine kontinuierliche Abbildung ƒ : X → Y von Polyedern heißt stückweise linear, wenn sie auf den Strahlen jeder Kegelumgebung eines beliebigen Punktes x ∈ wird als stückweise linearer Isomorphismus bezeichnet. Gegenstand der stückweise linearen Theorie ist die Untersuchung von Polyedern und ihren stückweise linearen Abbildungen. In der stückweise linearen Theorie gelten Polyeder als identisch, wenn sie stückweise linear isomorph sind.
Eine Teilmenge X ∈ |R n ist genau dann ein (kompaktes) Polyeder, wenn sie die Vereinigung einer (endlichen) Familie konvexer Polyeder ist. Jedes Polyeder kann als Vereinigung von Simplexen dargestellt werden, die sich nur entlang ganzer Flächen schneiden. Diese Darstellung wird Polyeder-Triangulation genannt. Jede Triangulation wird eindeutig durch ihr Simplizialschema bestimmt, das heißt durch die Menge aller ihrer Scheitelpunkte, in denen Teilmengen markiert sind, bei denen es sich um Scheitelpunktmengen von Simplexen handelt. Daher können wir anstelle von Polyedern nur einfache Schemata ihrer Triangulationen betrachten. Mithilfe eines einfachen Schemas können beispielsweise Homologie- und Kohomologiegruppen berechnet werden. Dies geschieht wie folgt:
a) ein Simplex, dessen Eckpunkte auf eine bestimmte Weise geordnet sind, wird als geordneter Simplex einer gegebenen Triangulation (oder eines Simplizialschemas) K bezeichnet; formale lineare Kombinationen geordneter Simplices einer gegebenen Dimension n mit Koeffizienten aus einer gegebenen Gruppe G werden n-dimensionale Ketten genannt; sie alle bilden natürlicherweise eine Gruppe, die mit dem Symbol C n (K; G) bezeichnet wird;
b) durch Eliminieren des Scheitelpunkts mit der Nummer i, 0 ≤ i ≤ n, aus dem geordneten n-dimensionalen Simplex σ erhalten wir einen geordneten (n-1)-dimensionalen Simplex, der durch das Symbol σ (i) bezeichnet wird; Kette
∂σ = σ (0) −σ (1) + ... +(−1) n σ (n) heißt Rand von σ; durch Linearität erstreckt sich die Abbildung ∂ auf den Homomorphismus ∂ : C n (K; G) → C n-1 (K; G);
c) Ketten c, für die ∂c = 0, heißen Zyklen; sie bilden eine Gruppe von Zyklen Z n (K; G);
d) Ketten der Form ∂c heißen Grenzen; sie bilden die Gruppe von Grenzen B n (K; G);
e) es ist bewiesen, dass B n (K; G) ⊂ Z n (K; G) (der Rand ist ein Kreis); daher ist die Faktorgruppe definiert
H n (K; G) = Z n (K; G)/ B n (K; G).
Es stellt sich heraus, dass die Gruppe H n (K; G) isomorph zur Homologiegruppe H n (X; G) des Polyeders X ist, dessen Triangulation K ist. Eine ähnliche Konstruktion, bei der man nicht von Ketten ausgeht, aber aus Cochains (beliebige Funktionen, die auf der Menge aller geordneten Simplices definiert sind und Werte in G annehmen), ergeben sich Kohomologiegruppen.
Mit dieser in leicht abgeänderter Form vorgelegten Konstruktion begann im Wesentlichen die Bildung des algebraischen T. In der ursprünglichen Konstruktion wurden die sogenannten orientierten Simplizes (Klassen geordneter Simplizes, die sich durch gerade Permutationen von Eckpunkten unterscheiden) berücksichtigt. Dieses Design wurde in den unterschiedlichsten Richtungen entwickelt und verallgemeinert. Insbesondere ihre algebraischen Aspekte führten zur sogenannten homologischen Algebra.
Im allgemeinsten Sinne kann ein Simplizialschema als eine Menge definiert werden, in der bestimmte endliche Teilmengen („Simplices“) markiert sind, und es ist erforderlich, dass jede Teilmenge eines Simplex wieder ein Simplex ist. Ein solches Simplizialschema ist genau dann ein Simplizialschema für die Triangulation eines Polyeders, wenn die Anzahl der Elemente einer beliebigen markierten Teilmenge eine feste Zahl nicht überschreitet. Das Konzept eines Polyeders kann jedoch verallgemeinert werden (nachdem man die sogenannten „unendlichdimensionalen Polyeder“ erhalten hat),
und dann ist jedes einfache Schema ein Triangulationsschema eines Polyeders (seine geometrische Realisierung genannt).
Eine beliebige offene Überdeckung (U α ) jedes topologischen Raums eine nicht leere Kreuzung. Dieses einfache Diagramm (und das entsprechende Polyeder) wird als Überdeckungsnerv bezeichnet. Die Nerven aller möglichen Hüllen nähern sich gewissermaßen dem Raum Diese Idee liegt fast allen Konstruktionen der allgemeinen Homologietheorie zugrunde. Auch im allgemeinen T spielt die Annäherung an den topologischen Raum durch die Nerven seiner offenen Hüllen eine wichtige Rolle.
5. Topologie von Mannigfaltigkeiten
Ein parakompakter topologischer Raum nach Hausdorff wird als n-dimensionale topologische Mannigfaltigkeit bezeichnet, wenn er „lokal euklidisch“ ist, d. In dieser Nachbarschaft werden Punkte durch n Zahlen x 1 angegeben,
..., x n, sogenannte lokale Koordinaten. Am Schnittpunkt zweier Karten werden die entsprechenden lokalen Koordinaten durch bestimmte Funktionen, sogenannte Übergangsfunktionen, zueinander ausgedrückt. Diese Funktionen definieren einen Homöomorphismus offener Mengen in |R n und werden Übergangshomöomorphismus genannt.
Wir vereinbaren, einen beliebigen Homöomorphismus zwischen offenen Mengen in |R n als t-Homöomorphismus zu bezeichnen. Ein Homöomorphismus, der ein stückweise linearer Isomorphismus ist, wird p-Homöomorphismus genannt, und wenn er durch glatte (beliebig oft differenzierbare) Funktionen ausgedrückt wird, nennen wir ihn s-Homöomorphismus.
Sei α = t, p oder s. Eine topologische Mannigfaltigkeit wird α-Mannigfaltigkeit genannt, wenn ihre Abdeckung mit Karten so gewählt ist, dass die Übergangshomöomorphismen für zwei beliebige ihrer (sich schneidenden) Karten α-Homöomorphismen sind. Eine solche Abdeckung definiert eine α-Struktur auf der topologischen Mannigfaltigkeit X.
Eine t-Mannigfaltigkeit ist also einfach jede topologische Mannigfaltigkeit, p-Mannigfaltigkeiten werden stückweise lineare Mannigfaltigkeiten genannt. Jede stückweise lineare Mannigfaltigkeit ist ein Polyeder. In der Klasse aller Polyeder zeichnen sich n-dimensionale stückweise lineare Mannigfaltigkeiten dadurch aus, dass jeder ihrer Punkte eine Nachbarschaft hat, die stückweise linear isomorph zum n-dimensionalen Würfel ist. S-Mannigfaltigkeiten werden glatte (oder differenzierbare) Mannigfaltigkeiten genannt. Eine α-Abbildung ist eine α-Mannigfaltigkeit, die als beliebige kontinuierliche Abbildung für α = t, als beliebige stückweise lineare Abbildung für α = s und als beliebige glatte Abbildung für α = s bezeichnet wird, also als kontinuierliche Abbildung in lokalen Koordinaten geschrieben durch glatte Funktionen.
Eine Eins-zu-eins-α-Abbildung, deren Umkehrung ebenfalls eine α-Abbildung ist, wird als α-Homöomorphismus bezeichnet (für α = s auch als Diffeomorphismus), die α-Mannigfaltigkeiten X und Y werden als α-homöomorph bezeichnet ( für α = s, diffeomorph), wenn es existiert, obwohl es eines gäbe
α-Homöomorphismus X → Y.
Gegenstand der Theorie der α-Mannigfaltigkeiten ist die Untersuchung von α-Mannigfaltigkeiten und ihrer α-Abbildungen; in diesem Fall werden α-homöomorphe α-Mannigfaltigkeiten als identisch betrachtet. Die Theorie der S-Mannigfaltigkeiten ist Teil des stückweise linearen T. Die Theorie der S-Mannigfaltigkeiten wird auch glattes T genannt.
Die Hauptmethode der modernen Mannigfaltigkeitstheorie besteht darin, ihre Probleme auf Probleme der algebraischen Theorie für bestimmte entsprechend konstruierte topologische Räume zu reduzieren. Diese enge Verbindung zwischen der Varietätstheorie und der algebraischen Theorie ermöglichte einerseits die Lösung vieler schwieriger geometrischer Probleme und stimulierte andererseits die Entwicklung der algebraischen Theorie selbst stark.
Beispiele für glatte Mannigfaltigkeiten sind n-dimensionale Flächen in |R n, die keine singulären Punkte haben. Es stellt sich heraus (Einbettungssatz), dass jede glatte Mannigfaltigkeit zu einer solchen Oberfläche diffeomorph ist (für N ≥ 2n + 1). Ein ähnliches Ergebnis gilt auch für α = t, p.
Jede p-Varietät ist eine t-Varietät. Es stellt sich heraus, dass man auf jeder s-Mannigfaltigkeit auf natürliche Weise eine p-Struktur einführen kann (was normalerweise als Aithead-Triangulation bezeichnet wird). Wir können sagen, dass jede α-Mannigfaltigkeit mit α = p oder s eine α’-Mannigfaltigkeit mit α’ = t oder p ist.
Die Antwort auf die umgekehrte Frage: Auf welchen α’-Mannigfaltigkeiten können wir eine α-Struktur einführen (eine solche α’-Mannigfaltigkeit mit α’ = p heißt glatt und mit α’ = t – trianguliert),
und wenn möglich, wie viel dann? - hängt von der Dimension n ab.
Es gibt nur zwei eindimensionale topologische Mannigfaltigkeiten: den Kreis S 1 (kompakte Mannigfaltigkeit) und die Gerade |R (nichtkompakte Mannigfaltigkeit). Für jedes α = p, s gibt es eine eindeutige α-Struktur auf den t-Mannigfaltigkeiten S 1 und |R.
In ähnlicher Weise gibt es auf jeder zweidimensionalen topologischen Mannigfaltigkeit (Oberfläche) eine eindeutige α-Struktur, und alle kompakten verbundenen Oberflächen können leicht beschrieben werden (nichtkompakte verbundene Oberflächen können ebenfalls beschrieben werden, die Antwort ist jedoch komplexer). Damit Oberflächen homöomorph sind, reicht es aus, dass sie homotopieäquivalent sind. Darüber hinaus wird der Homotopietyp jeder Oberfläche eindeutig durch ihre Homologiegruppen charakterisiert. Es gibt zwei Arten von Oberflächen: orientierbare und nicht orientierbare. Zu den Orientierungskörpern zählen die Sphäre SI und der Torus TI. Seien X und Y zwei zusammenhängende n-dimensionale α-Mannigfaltigkeiten.
Schneiden wir eine Kugel in X und Y aus (für n = 2 – eine Scheibe) und kleben wir die resultierenden Randkugeln (für n = 2 – Kreise) zusammen. Vorbehaltlich einiger selbstverständlicher Vorsichtsmaßnahmen ist das Ergebnis wiederum eine α-Mannigfaltigkeit.
Sie wird als zusammenhängende Summe der α-Mannigfaltigkeiten X und Y bezeichnet und mit X#Y bezeichnet. TI#TI hat beispielsweise die Form einer Brezel. Die Sphäre S n ist die Nullstelle dieser Addition, d. h. S n #X = X für jedes X. Insbesondere ist SІ#TI = TI. Es stellt sich heraus, dass die orientierbare Oberfläche homöomorph zu einer zusammenhängenden Summe der Form SІ#TI# ist
...#TI, die Anzahl p der Terme TI wird als Gattung der Oberfläche bezeichnet. Für eine Kugel gilt p = 0, für einen Torus p = 1 usw. Eine Oberfläche der Gattung p kann man sich als Kugel vorstellen, an die p „Griffe“ geklebt sind.
Jede nicht orientierbare Fläche ist homöomorph zu einer zusammenhängenden Summe |RPI#... #|RPI einer bestimmten Anzahl projektiver Ebenen |RPI. Man kann es sich als Kugel vorstellen, auf die mehrere Möbius-Blätter geklebt sind.
Auf jeder dreidimensionalen topologischen Mannigfaltigkeit für jedes α = p, s gibt es auch eine eindeutige α-Struktur und es ist möglich, alle Homotopietypen dreidimensionaler topologischer Mannigfaltigkeiten zu beschreiben (hierfür reichen Homologiegruppen jedoch nicht mehr aus). Gleichzeitig wurden bis heute (1976) nicht alle (zumindest kompakt zusammenhängenden) Poincaré-Vermutungen beschrieben, es ist unbekannt.
Bemerkenswert ist, dass sich die Situation für kompakte und zusammenhängende topologische Varietäten der Dimension n ≥ 5 völlig anders darstellt: Alle Hauptprobleme für sie können als prinzipiell gelöst (genauer gesagt reduziert auf Probleme der algebraischen Theorie) angesehen werden. Jede glatte Mannigfaltigkeit X ist als glatte (n-dimensionale) Oberfläche in IR N eingebettet, und die Tangentenvektoren an Ein topologischer Raum X heißt topologischer Raum E, für den eine solche kontinuierliche Abbildung gegeben ist
π : E → X, sodass für jeden Punkt x ∈ X das Umkehrbild von v (Schicht) ein Vektorraum ist und es eine offene Überdeckung (U α ) des Raums
π −1 (U α) ist homöomorph zum Produkt U α × |R n , und es gibt einen Homöomorphismus π −1 (U α) → U α × |R n , der jede Schicht linear abbildet
π −1 (x), x ∈ U α, zum Vektorraum (x) H |R n. Wenn E = TX, ordnet die kontinuierliche Karte π jedem Tangentenvektor den Punkt seiner Tangente zu, sodass die Ebene
π −1 (x) ist der Raum tangential zu X im Punkt x. Es stellt sich heraus, dass jedes Vektorbündel über einem kompakten Raum X ein Element der Gruppe KO(X) definiert. Somit ist insbesondere für jede glatte, kompakte und zusammenhängende Mannigfaltigkeit X in der Gruppe KO(X) ein Element definiert, das dem Tangentenbündel entspricht. Man nennt sie die Tangentialinvariante einer glatten Varietät X. Für jedes α gibt es ein Analogon dieser Konstruktion.
Für α = p wird die Rolle der Gruppe KO(X) von einer anderen Gruppe mit der Bezeichnung KPL(X) übernommen, und für α = t wird die Rolle dieser Gruppe von einer Gruppe mit der Bezeichnung KTop(X) übernommen. Jede α-Mannigfaltigkeit X definiert in der entsprechenden Gruppe [KO(X), KPL(X) oder KTop(X)] ein Element, das als seine α-tangentiale Invariante bezeichnet wird.
Es gibt natürliche Homomorphismen KO(X) → KPL(X) → KTop(X), und es stellt sich heraus, dass auf einer n-dimensionalen (n ≥ 5) kompakten und zusammenhängenden α-Mannigfaltigkeit X, wobei α = t, p, if und nur wenn man eine α-Struktur einführen kann (α = p, wenn α = t, und α = s, wenn α = p), wenn ihre α-tangentiale Invariante im Bild der entsprechenden Gruppe liegt.
Die Anzahl solcher Strukturen ist endlich und gleich der Anzahl der Elemente einer Faktormenge der Menge, wobei Y α ein speziell konstruierter topologischer Raum ist (für α = s wird der topologische Raum Y α normalerweise mit dem Symbol PL/ bezeichnet) O, und für α = p - durch das Symbol Top/PL).
Damit wird die Frage nach der Existenz und Einzigartigkeit einer α-Struktur auf ein bestimmtes Problem der Homotopietheorie reduziert. Der Homotopietyp des topologischen Raums PL/O ist recht kompliziert und noch nicht vollständig berechnet (1976); Das ist jedoch bekannt
π i (PL/O) = 0 für i ≤ 6, daraus folgt, dass jede stückweise lineare Mannigfaltigkeit der Dimension n ≤ 7 glättbar ist, und zwar für n ≤ 6 auf eindeutige Weise. Im Gegenteil erweist sich der Homotopietyp des topologischen Raums Top/PL als überraschend einfach: Dieser Raum ist homotopieäquivalent zu K(ℤ 2 , 3).
Folglich übersteigt die Anzahl der stückweise linearen Strukturen auf einer topologischen Mannigfaltigkeit nicht die Anzahl der Elemente der Gruppe H i(X, ℤ 2). Solche Strukturen existieren sicherlich, wenn H 4 (X, ℤ 2)
= 0, aber für H 4 (X, ℤ 2) ≠ 0 existiert die stückweise lineare Struktur möglicherweise nicht.
Insbesondere gibt es eine einzigartige stückweise lineare Struktur auf der Sphäre S n. Auf der Kugel S n kann es viele glatte Strukturen geben, auf S 7 gibt es beispielsweise 28 verschiedene glatte Strukturen. Auf dem Torus T n (dem topologischen Produkt von n Kopien des Kreises S 1) existieren für n ≥ 5 viele verschiedene stückweise lineare Strukturen, die alle eine glatte Struktur zulassen.
Somit entspricht die erste der Kugel und ist zu ihr homöomorph.
Neben α-Mannigfaltigkeiten können wir auch sogenannte α-Mannigfaltigkeiten mit Rand betrachten; Sie zeichnen sich dadurch aus, dass die Umgebungen einiger ihrer Punkte (die die Kante bilden) α-homöomorph zum Halbraum X n ≥ 0 des Raums |R n sind. Eine Grenze ist eine (n-1)-dimensionale α-Mannigfaltigkeit (im Allgemeinen unzusammenhängend).
Zwei n-dimensionale kompakte α-Mannigfaltigkeiten homöomorph zu X und Y .
Wenn die Einbettungskarten X → W und Y → W Homotopieäquivalenzen sind, dann heißen die glatten Mannigfaltigkeiten h-kobordant. Mithilfe von Handle-Zerlegungsmethoden lässt sich beweisen, dass für n ≥ 5 einfach zusammenhängende kompakte α-Mannigfaltigkeiten α-homöomorph sind, wenn sie h-kobordant sind.
Dieses h-Cobordismus-Theorem bietet die stärkste Möglichkeit, die α-Homöomorphie von α-Mannigfaltigkeiten zu beweisen (insbesondere ist die Poincaré-Vermutung eine Folge davon). Ein ähnliches, aber komplexeres Ergebnis gilt auch für nicht einfach zusammenhängende α-Mannigfaltigkeiten.
Die Sammlung von n Klassen kobordanter kompakter α-Mannigfaltigkeiten ist eine kommutative Gruppe in Bezug auf die verbundene Summenoperation. Der Nullpunkt dieser Gruppe ist die Klasse der α-Mannigfaltigkeiten, die Kanten sind, also mit Null kobordant sind. Es stellt sich heraus, dass diese Gruppe für α = s isomorph zur Homotopiegruppe π 2n+1 MO (n+1) eines speziell konstruierten topologischen Raums MO (n+1), dem sogenannten Thom-Raum, ist.
Ein ähnliches Ergebnis ergibt sich für α = p, t. Daher ermöglichen die Methoden der algebraischen Theorie grundsätzlich die Berechnung der Gruppe α n. Insbesondere stellt sich heraus, dass die Gruppe s n eine direkte Summe von Gruppen ℤ 2 in einer Menge ist, die der Anzahl der Partitionen der Zahl n in andere Terme als Zahlen der Form 2 m -1 entspricht. Zum Beispiel ist s 3 = 0 (also ist jede dreidimensionale kompakte glatte Mannigfaltigkeit eine Grenze).
Im Gegenteil, s 2 = ℤ 2, es gibt also Flächen, die zueinander kobordant und nicht zu Null kobordant sind; Eine solche Fläche ist beispielsweise die projektive Ebene |RP I.
M. M. Postnikov.
6. Hauptphasen der Topologieentwicklung
Einige Ergebnisse topologischer Natur wurden bereits im 18. und 19. Jahrhundert gewonnen. (Eulers Satz über konvexe Polyeder, Klassifizierung von Oberflächen und Jordans Satz, dass eine einfache geschlossene Linie, die in einer Ebene liegt, die Ebene in zwei Teile teilt). Zu Beginn des 20. Jahrhunderts. Es entsteht ein allgemeines Konzept des Raumes im Raum (metrisch – M. Fréchet, topologisch – F. Hausdorff) und unter dem Einfluss der Elemente entsteht eine (bi)kompakte Erweiterung eines völlig regelmäßigen Raumes; Homologiegruppen beliebiger Räume werden definiert (Cech), in Kohomologiegruppen (J. Homotopietheorie (H. Hopf, Pontryagin); Homotopiegruppen werden definiert (V. in Frankreich, M. M. Postnikov in der UdSSR, Whitehead usw.) die Theorie wird schließlich Homotopien gebildet. Zu dieser Zeit wurden in den USA große Zentren der algebraischen Topologie und der Triangulabilität geschaffen (J. Milnor, USA). A, Differential Topology. Beginning Course, übersetzt aus dem Englischen, Moskau, 1972; Steenrod N., Chinn W., Erste Konzepte der Topologie, übersetzt aus dem Englischen, M., 1967; Alexandrov P. S., Kombinatorische Topologie, M.-L., 1947; Alexandrov P. S., Pasynkov B. A., Einführung in die Dimensionstheorie.
Einführung in die Theorie topologischer Räume und die allgemeine Dimensionstheorie, M., 1973; Aleksandrov P.S., Einführung in die homologische Dimensionstheorie und allgemeine kombinatorische Topologie, M., 1975; Arkhangelsky A.V., Ponomarev V.I., Grundlagen der allgemeinen Topologie in Problemen und Übungen, M., 1974; Postnikov M. M., Einführung in die Morsetheorie, M., 1971; Bourbaki N., Allgemeine Topologie. Grundstrukturen, trans. aus Französisch, M., 1968; seine, Allgemeine Topologie. Topologische Gruppen. Zahlen und verwandte Gruppen und Räume, trans. aus Französisch, M., 1969; seine, Allgemeine Topologie.
Ein Computernetzwerk kann in zwei Komponenten unterteilt werden. Ein physisches Computernetzwerk ist in erster Linie eine Ausrüstung. Das heißt, alle erforderlichen Kabel und Adapter, die an Computer, Hubs, Switches, Drucker usw. angeschlossen sind. Alles, was in einem gemeinsamen Netzwerk funktionieren sollte.
Die zweite Komponente eines Computernetzwerks ist das logische Netzwerk. Hierbei handelt es sich um das Prinzip der Verbindung mehrerer Computer und der erforderlichen Geräte zu einem einzigen System (die sogenannte Computernetzwerktopologie). Dieses Konzept ist eher auf lokale Netzwerke anwendbar. Es ist die gewählte Topologie für die Verbindung mehrerer Computer, die Einfluss auf die erforderliche Ausrüstung, die Zuverlässigkeit des Netzwerks, die Möglichkeit seiner Erweiterung und die Arbeitskosten hat. Heutzutage sind Ring-, Stern- und Bustopologien die am weitesten verbreiteten Arten von Computernetzwerktopologien. Letzteres ist jedoch fast außer Gebrauch geraten.
Stern, Ring und Bus sind die Grundtopologien von Computernetzwerken.
"Stern"
Die Topologie von Computernetzwerken „Stern“ ist eine Struktur, deren Zentrum ein Schaltgerät ist. Alle Computer sind über separate Leitungen daran angeschlossen.
Das Schaltgerät kann ein Hub, also ein HUB, oder ein Switch sein. Diese Topologie wird auch „Passivstern“ genannt. Wenn es sich bei dem Schaltgerät um einen anderen Computer oder Server handelt, kann die Topologie als „aktiver Stern“ bezeichnet werden. Es ist das Schaltgerät, das das Signal von jedem Computer empfängt, verarbeitet und an andere angeschlossene Computer sendet.
Diese Topologie hat eine Reihe von Vorteilen. Der unbestrittene Vorteil besteht darin, dass die Computer nicht voneinander abhängig sind. Fällt einer von ihnen aus, bleibt das Netzwerk selbst funktionsfähig. Sie können auch problemlos einen neuen Computer an ein solches Netzwerk anschließen. Wenn neue Geräte angeschlossen werden, funktionieren die übrigen Elemente des Netzwerks wie gewohnt weiter. In dieser Art von Netzwerktopologie ist es einfach, Fehler zu finden. Einer der Hauptvorteile des „Sterns“ ist vielleicht seine hohe Leistung.
Doch trotz aller Vorteile hat diese Art von Computernetzwerk auch Nachteile. Fällt die zentrale Schalteinrichtung aus, fällt das gesamte Netzwerk aus. Es gibt Einschränkungen für angeschlossene Workstations. Es dürfen nicht mehr als die verfügbare Anzahl an Ports auf dem Switch-Gerät vorhanden sein. Und der letzte Nachteil des Netzwerks sind seine Kosten. Für die Verbindung jedes Computers ist eine relativ große Menge Kabel erforderlich.
"Ring"
Die Topologie des Computernetzwerks „Ring“ hat kein strukturelles Zentrum. Hier sind alle Arbeitsplätze samt Server in einem geschlossenen Kreis vereint. In diesem System bewegt sich das Signal sequentiell im Kreis von rechts nach links. Alle Computer sind Repeater, sodass das Markierungssignal aufrechterhalten und weiter übertragen wird, bis es den Empfänger erreicht.

Auch diese Art der Topologie hat sowohl Vor- als auch Nachteile. Der Hauptvorteil besteht darin, dass der Betrieb des Computernetzwerks auch unter hoher Belastung stabil bleibt. Diese Art von Netzwerk ist sehr einfach zu installieren und erfordert nur ein Minimum an zusätzlicher Ausrüstung.
Im Gegensatz zur „Stern“-Topologie kann bei der „Ring“-Topologie der Betrieb des gesamten Systems durch den Ausfall eines angeschlossenen Computers lahmgelegt werden. Darüber hinaus wird es viel schwieriger sein, die Fehlfunktion zu identifizieren. Trotz der einfachen Installation dieser Netzwerkoption ist ihre Konfiguration recht komplex und erfordert bestimmte Fähigkeiten. Ein weiterer Nachteil dieser Topologie ist die Notwendigkeit, das gesamte Netzwerk auszusetzen, um neue Geräte anzuschließen.
"Reifen"
Die Bustopologie von Computernetzwerken wird immer seltener. Es besteht aus einem einzigen langen Backbone, an den alle Computer angeschlossen sind.

In diesem System, wie auch in anderen, werden die Daten zusammen mit der Adresse des Empfängers gesendet. Alle Computer empfangen das Signal, es wird jedoch direkt vom Empfänger empfangen. Durch eine Bustopologie verbundene Arbeitsplätze können nicht gleichzeitig Datenpakete versenden. Während einer der Computer diese Aktion ausführt, warten die anderen, bis sie an der Reihe sind. Die Signale bewegen sich entlang der Leitung in beide Richtungen, doch am Ende werden sie reflektiert und überlappen sich, wodurch der reibungslose Betrieb des gesamten Systems gefährdet wird. Es gibt spezielle Geräte – Terminatoren, die Signale dämpfen sollen. Sie werden an den Enden der Autobahn installiert.
Zu den Vorteilen der „Bus“-Topologie gehört, dass ein solches Netzwerk recht schnell installiert und konfiguriert werden kann. Darüber hinaus ist die Installation recht kostengünstig. Fällt einer der Computer aus, läuft das Netzwerk wie gewohnt weiter. Der Anschluss neuer Geräte kann funktionsfähig erfolgen. Das Netzwerk wird funktionieren.
Wenn das Zentralkabel beschädigt ist oder einer der Abschlusswiderstände nicht mehr funktioniert, führt dies zu einer Abschaltung des gesamten Netzwerks. Es ist ziemlich schwierig, in einer solchen Topologie einen Fehler zu finden. Eine Erhöhung der Anzahl der Arbeitsplätze verringert die Netzwerkleistung und führt zudem zu Verzögerungen bei der Informationsübertragung.
Abgeleitete Computernetzwerktopologien
Die Klassifizierung von Computernetzwerken nach Topologie ist nicht auf drei grundlegende Optionen beschränkt. Es gibt auch Topologietypen wie „Linie“, „Doppelring“, „Netztopologie“, „Baum“, „Gitter“, „Enges Netzwerk“, „Schneeflocke“ und „vollständig verbundene Topologie“. Sie alle sind von den Grundprinzipien abgeleitet. Schauen wir uns einige Optionen an.
Ineffiziente Topologien
In einer Mesh-Topologie sind alle Arbeitsplätze miteinander verbunden. Ein solches System ist ziemlich umständlich und ineffektiv. Es ist erforderlich, jedem Computerpaar eine Leitung zuzuweisen. Diese Topologie wird nur in Mehrmaschinensystemen verwendet.
Die Mesh-Topologie ist tatsächlich eine abgespeckte Version der vollständig verbundenen Topologie. Auch hier sind alle Computer über separate Leitungen miteinander verbunden.

Effizienteste Topologien
Die „Schneeflocke“ genannte Topologie zum Aufbau von Computernetzwerken ist eine abgespeckte Version des „Sterns“. Dabei fungieren sternförmig miteinander verbundene Hubs als Arbeitsstationen. Diese Topologieoption gilt als eine der optimalsten für große lokale und globale Netzwerke.
Sowohl große lokale als auch globale Netzwerke verfügen in der Regel über eine große Anzahl von Subnetzen, die auf unterschiedlichen Topologietypen aufgebaut sind. Dieser Typ wird als gemischt bezeichnet. Hier kann man gleichzeitig den „Stern“, den „Reifen“ und den „Ring“ unterscheiden.

Im obigen Artikel wurden daher alle wichtigen verfügbaren Computernetzwerktopologien, die in lokalen und globalen Netzwerken verwendet werden, sowie ihre Variationen, Vor- und Nachteile betrachtet.
Erklärendes Wörterbuch der russischen Sprache. D.N. Uschakow
Topologie
Topologie, viele Jetzt. (von griech. topos – Ort und logos – Lehre) (mat.). Teil der Geometrie, der die qualitativen Eigenschaften von Figuren untersucht (d. h. unabhängig von Konzepten wie Länge, Winkel, Geradheit usw.).
Neues erklärendes Wörterbuch der russischen Sprache, T. F. Efremova.
Topologie
Und. Ein Zweig der Mathematik, der die qualitativen Eigenschaften geometrischer Figuren untersucht, unabhängig von ihrer Länge, ihrem Winkel, ihrer Geradheit usw.
Enzyklopädisches Wörterbuch, 1998
Topologie
TOPOLOGIE (von griechisch topos – Ort und... Logik) ist ein Zweig der Mathematik, der die topologischen Eigenschaften von Figuren untersucht, d.h. Eigenschaften, die sich bei Verformungen nicht ändern, die ohne Brüche und Verklebungen (genauer gesagt mit Eins-zu-Eins- und kontinuierlichen Abbildungen) erzeugt werden. Beispiele für topologische Eigenschaften von Figuren sind die Dimension, die Anzahl der Kurven, die eine bestimmte Fläche begrenzen usw. Somit haben ein Kreis, eine Ellipse und der Umriss eines Quadrats die gleichen topologischen Eigenschaften, weil diese Linien können in der oben beschriebenen Weise ineinander verformt werden; Gleichzeitig haben Ring und Kreis unterschiedliche topologische Eigenschaften: Der Kreis wird durch eine Kontur begrenzt, der Ring durch zwei.
Topologie
(aus dem Griechischen topos ≈ Ort und ¼ logie) ≈ Teil der Geometrie, der sich mit dem Studium des Phänomens der Kontinuität befasst (ausgedrückt beispielsweise im Begriff der Grenze). Die Vielfalt der Erscheinungsformen der Kontinuität in der Mathematik und eine Vielzahl unterschiedlicher Ansätze zu ihrer Untersuchung führten zum Zerfall der einheitlichen Mathematik in eine Reihe von Abteilungen („allgemeine Mathematik“, „algebraische Mathematik“ usw.), die sich voneinander unterscheiden Gegenstand und Methode des Studiums und tatsächlich sehr wenig miteinander verbunden. I. Allgemeine Topologie Der Teil der Theorie, der auf das axiomatische Studium der Kontinuität ausgerichtet ist, wird als Allgemeine Theorie bezeichnet. Die Allgemeine Theorie bildet neben der Algebra die Grundlage der modernen mengentheoretischen Methode in der Mathematik. Axiomatisch kann Kontinuität auf viele (im Allgemeinen ungleiche) Arten definiert werden. Eine allgemein anerkannte Axiomatik basiert auf dem Konzept einer offenen Menge. Eine topologische Struktur oder Topologie auf einer Menge X ist eine Familie ihrer Teilmengen, sogenannte offene Mengen, so dass: 1) die leere Menge Æ und alle X offen sind; 2) Die Vereinigung einer beliebigen Zahl und der Durchschnitt einer endlichen Anzahl offener Mengen ist offen. Eine Menge, auf der eine topologische Struktur gegeben ist, wird topologischer Raum genannt. Im topologischen Raum X kann man alle Grundkonzepte der Elementaranalysis im Zusammenhang mit der Kontinuität definieren. Beispielsweise ist eine Umgebung eines Punktes x О X eine beliebige offene Menge, die diesen Punkt enthält; eine Menge A Ì X heißt geschlossen, wenn ihr Komplement X \ A offen ist; der Abschluss einer Menge A ist die kleinste abgeschlossene Menge, die A enthält; Wenn dieser Abschluss mit X zusammenfällt, heißt A überall in X dicht usw. Per Definition sind Æ und X sowohl geschlossene als auch offene Mengen. Wenn es in X keine anderen Mengen gibt, die sowohl geschlossen als auch offen sind, dann heißt der topologische Raum X zusammenhängend. Ein visuell verbundener Raum besteht aus einem „Stück“, während ein nicht verbundener Raum aus mehreren besteht. Jede Teilmenge A eines topologischen Raums X hat eine natürliche topologische Struktur, die aus Schnittpunkten mit A offener Mengen aus Seien Sie Mengen, die zusammen mit einem beliebigen Punkt einige seiner e-Umgebung enthalten (eine Kugel mit dem Radius e, die in diesem Punkt zentriert ist). Insbesondere ist jede Teilmenge eines n-dimensionalen euklidischen Raums ein topologischer Raum. Die Theorie solcher Räume (unter dem Namen „geometrische Theorie“) und die Theorie metrischer Räume gehören traditionell zur allgemeinen Theorie. Die geometrische Theorie gliedert sich ganz klar in zwei Teile: die Untersuchung von Teilmengen beliebiger Komplexität, vorbehaltlich bestimmter Einschränkungen allgemeiner Natur (ein Beispiel ist die sogenannte Theorie der Kontinua, d. h. verbundener begrenzter geschlossener Mengen) und die Untersuchung der Art und Weise, wie einfache topologische Räume wie eine Kugel, ein Ball usw. in ═ eingebettet werden können. (Investitionen beispielsweise in Kugeln können sehr komplex sein). Eine offene Überdeckung eines topologischen Raums X ist eine Familie seiner offenen Mengen, deren Vereinigung die Gesamtheit von X ist. Ein topologischer Raum aus Elementen, die auch die Hülle bilden. Der klassische Satz von Heine ≈ Borel besagt, dass jede begrenzte abgeschlossene Teilmenge ═kompakt ist. Es stellt sich heraus, dass alle Grundsätze der Elementaranalysis über begrenzte abgeschlossene Mengen (z. B. der Satz von Weierstrass, dass auf einer solchen Menge eine stetige Funktion ihren größten Wert erreicht) für alle kompakten topologischen Räume gelten. Dies bestimmt die grundlegende Rolle, die kompakte Räume in der modernen Mathematik spielen (insbesondere im Zusammenhang mit Existenzsätzen). Die Identifizierung der Klasse kompakter topologischer Räume war eine der größten Errungenschaften der Allgemeinen Theorie und hatte allgemeine mathematische Bedeutung. Eine offene Abdeckung (Vb) heißt in einer Abdeckung (Ua) eingeschrieben, wenn für jedes b ein a existiert, sodass Vb Ì Ua ist. Eine Überdeckung (Vb) heißt lokal endlich, wenn jeder Punkt x Î X eine Umgebung hat, die sich nur mit endlich vielen Elementen dieser Überdeckung schneidet. Ein topologischer Raum heißt parakompakt, wenn jede offene Überdeckung eine lokal endliche Überdeckung enthalten kann. Die Klasse der parakompakten Räume ist ein Beispiel für Klassen topologischer Räume, die durch Auferlegen sogenannter Kompaktheitstypbedingungen erhalten werden. Diese Klasse ist sehr umfangreich; insbesondere enthält sie alle metrisierbaren topologischen Räume, also Räume X, in denen es möglich ist, eine Metrik r so einzuführen, dass das von r in einer offenen Überdeckung ist die größte Zahl k, so dass es k ihrer Elemente gibt, die einen nichtleeren Schnittpunkt haben. Die kleinste Zahl n, die die Eigenschaft hat, dass eine offene Hülle der Multiplizität £n + 1 in jede endliche offene Hülle eines topologischen Raums X eingeschrieben werden kann, wird mit dem Symbol dimX bezeichnet und heißt Dimension von X. Dieser Name ist begründet durch die Tatsache, dass dimX in elementaren geometrischen Situationen mit der üblichen verständlichen Dimension übereinstimmt, zum Beispiel dim = n. Es sind auch andere numerische Funktionen des topologischen Raums X möglich, die sich von dimX unterscheiden, aber im einfachsten Fall mit dimX zusammenfallen. Ihre Untersuchung ist Gegenstand der Allgemeinen Dimensionstheorie, dem geometrisch am stärksten orientierten Teil des Allgemeinen T. Nur im Rahmen dieser Theorie ist es beispielsweise möglich, den intuitiven Begriff einer geometrischen Figur und insbesondere den Begriff einer Linie, Fläche usw. klar und recht allgemein zu definieren. Wichtige Klassen topologischer Räume erhält man durch die Einführung der sogenannten Trennungsaxiome. Ein Beispiel ist das sogenannte Hausdorff-Axiom oder Axiom T2, das erfordert, dass zwei beliebige unterschiedliche Punkte disjunkte Nachbarschaften haben. Ein topologischer Raum, der dieses Axiom erfüllt, wird Hausdorff oder separierbar genannt. In der mathematischen Praxis sind seit einiger Zeit fast ausschließlich Hausdorff-Räume anzutreffen (z. B. ist jeder metrische Raum Hausdorff-Raum). Die Rolle topologischer Nicht-Hausdorff-Räume in Analysis und Geometrie nimmt jedoch ständig zu. Topologische Räume, die Teilräume von Hausdorff(bi)kompakten Räumen sind, werden vollständig regulär oder Tichonow genannt. Sie können auch durch ein Axiom der Trennbarkeit charakterisiert werden, nämlich: ein Axiom, das verlangt, dass für jeden Punkt x0 ═X und jede abgeschlossene Menge F ═X, die ihn nicht enthält, eine stetige Funktion g: X ╝ gleich Null bei x0 und Eins existiert auf F. Topologische Räume, die offene Unterräume von Hausdorff-kompakten Räumen sind, werden lokal kompakte Räume genannt. Sie zeichnen sich (in der Klasse der Hausdorff-Räume) dadurch aus, dass jeder ihrer Punkte eine Umgebung mit kompaktem Abschluss hat (Beispiel: Euklidischer Raum). Jeder solche Raum wird durch einen Punkt zu einem kompakten ergänzt (Beispiel: Durch Addition eines Punktes aus der Ebene erhält man eine Kugel einer komplexen Variablen und aus ═≈ eine Kugel S n). Eine Abbildung f:X ╝ Y von einem topologischen Raum wenn es eins zu eins ist und die inverse Abbildung f≈ 1: Y ╝ X stetig ist. Eine solche Abbildung stellt eine Eins-zu-eins-Entsprechung zwischen offenen Mengen topologischer Räume X und Y her, die mit den Operationen Vereinigung und Schnittmenge von Mengen permutierbar ist. Daher sind alle topologischen Eigenschaften (d. h. Eigenschaften, die als offene Mengen formuliert werden) dieser Räume gleich, und aus topologischer Sicht sind homöomorphe topologische Räume (d. h. Räume, für die es mindestens einen Homöomorphismus X gibt) ╝ Y) sollten als gleich angesehen werden (so wie in der euklidischen Geometrie Figuren, die durch Bewegung kombiniert werden können, als identisch gelten). Beispielsweise sind Kreis und Rand eines Quadrats, Sechsecks usw. homöomorph („topologisch identisch“). Im Allgemeinen sind zwei beliebige einfache (ohne Doppelpunkte) geschlossene Geraden homöomorph. Im Gegenteil, ein Kreis ist nicht homöomorph zu einer geraden Linie (weil das Entfernen eines Punktes nicht den Zusammenhang des Kreises verletzt, wohl aber den Zusammenhang der geraden Linie; aus dem gleichen Grund ist eine gerade Linie nicht homöomorph zu a Ebene, und ein Kreis ist nicht homöomorph zu einer Acht). Ein Kreis ist auch nicht homöomorph zu einer Ebene (wirf nicht einen, sondern zwei Punkte weg). Sei (Xa) ≈ eine beliebige Familie topologischer Räume. Betrachten Sie die Menge X aller Familien der Form (xa), wobei xa ═Xa (das direkte Produkt der Mengen Xa). Für jedes a definiert die Formel eine Zuordnung ═ (sogenannte Projektion). Im Allgemeinen kann man in X viele topologische Strukturen einführen, bezüglich derer alle Abbildungen pa stetig sind. Unter diesen Strukturen gibt es die kleinste (die in jeder solchen Struktur enthalten ist). Die mit dieser topologischen Struktur ausgestattete Menge X heißt topologisches Produkt topologischer Räume Xa und wird mit dem Symbol PHa (und im Fall einer endlichen Anzahl von Faktoren mit dem Symbol Explizit können offene Mengen des Raums X als Vereinigungen endlicher Durchschnitte aller Mengen der Form beschrieben werden, in denen Ua in Xa offen ist. Der topologische Raum A. Der Raum ═ist das topologische Produkt von n Instanzen der Zahlenlinie. Einer der wichtigsten Sätze der Allgemeinen Theorie ist die Aussage, dass das topologische Produkt kompakter topologischer Räume kompakt ist. Wenn X ≈ topologischer Raum und Y ≈ eine beliebige Menge ist und eine Abbildung p: p ist eine natürliche Projektionsabbildung auf jedes Element x Î X ist seine Äquivalenzklasse), dann können wir die Frage aufwerfen, in Y eine topologische Struktur einzuführen, bezüglich der die Abbildung p stetig ist. Die „reichste“ (an offenen Mengen) solche Struktur erhält man, wenn man alle Mengen V Ì Y, für die die Menge f-1(V) Ì X in X offen ist, als offene Mengen in Y betrachtet. Die damit ausgestattete Menge Y Die topologische Struktur wird als Quotientenraum des topologischen Raums X (relativ zu p) bezeichnet. Es hat die Eigenschaft, dass eine beliebige Abbildung f: Y ╝ Z genau dann stetig ist, wenn die Abbildung ═: X ╝ Z stetig ist. Eine stetige Abbildung p: X ╝ Y heißt Faktor, wenn der topologische Raum Y ein Faktorraum von ist der topologische Raum bezüglich p X. Eine stetige Abbildung p: X ╝ Y heißt offen, wenn für jede offene Menge U Ì Menge p(F) ist in Y abgeschlossen. Wie offene und geschlossene stetige Abbildungen f:X ╝ Y, für die f(X) = Y faktoriell sind. Sei X ≈ ein topologischer Raum, A ≈ sein Unterraum und f: A ╝ Y ≈ eine kontinuierliche Abbildung. Unter der Annahme, dass die topologischen Räume X und Y disjunkt sind, führen wir eine topologische Struktur in ihrer Vereinigung X È Y ein und betrachten die Vereinigungen offener Mengen aus Beziehung, in der a ~ f(a) für jeden Punkt a Î A. Der entsprechende Quotientenraum wird mit dem Symbol X È fY bezeichnet und soll durch Kleben des topologischen Raums X mit dem topologischen Raum Y entlang A durch erhalten werden mittels einer kontinuierlichen Karte f. Dieser einfache und intuitive Vorgang erweist sich als sehr wichtig, da er es ermöglicht, aus relativ einfachen topologischen Räumen komplexere Werte zu erhalten. Besteht Y aus einem Punkt, so wird der Raum X È fY mit dem Symbol X/A bezeichnet und man sagt, er ergebe sich aus Wenn beispielsweise X ≈ eine Scheibe und A ≈ ihr Grenzkreis, dann ist X/A homöomorph zu einer Kugel. 2. Einheitliche Topologie Der Teil der Theorie, der sich mit dem axiomatischen Konzept der gleichmäßigen Stetigkeit befasst, wird als einheitliche Theorie bezeichnet. Die aus der Analysis bekannte Definition der gleichmäßigen Stetigkeit numerischer Funktionen wird direkt auf Abbildungen beliebiger metrischer Räume übertragen. Daher wird die Axiomatik der gleichmäßigen Kontinuität normalerweise ausgehend von metrischen Räumen erhalten. Zwei axiomatische Ansätze zur gleichmäßigen Kontinuität, die auf den Konzepten der Nähe bzw. der diagonalen Einkreisung basieren, werden im Detail untersucht. Teilmengen A und B des metrischen Raums< e. Принимая основные свойства этого отношения за аксиомы, приходят к следующему определению: (отделимой) структурой близости на множестве Х называется такое отношение d на множестве всех его подмножеств, что: 1) ÆX (символом обозначается отрицание отношения d; 2) AB1 и AB2Û A(B1 U B2); ═3) {x}{y} Û x ¹ y;4) если АВ, то существует такое множество С В, что А(Х\С). Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости Х в пространство близости Y называется близостно непрерывным, если образы близких в Х множеств близки в Y. Пространства близости Х и Y называются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение X ╝ Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Т. эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество u Ì x открытым, если {x}(X \U) для любой точки х Î U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства Х все структуры близости на X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии ≈ би-компактными расширениями) вХ ≈ компактными хаусдорфовыми топологическими пространствами, содержащими Х в качестве всюду плотного пространства. Структура близости d, соответствующая расширению вХ, характеризуется тем, что АdВ тогда и только тогда, когда замыкания множеств А и В пересекаются в bX. В частности, на любом компактном хаусдорфовом топологическом пространстве Х существует единственная структура близости, порождающая его топологическую структуру. Другой подход основан на том, что равномерную непрерывность в метрическом пространстве Х можно определить в терминах отношения «точки х и у находятся на расстоянии, не большем e». С общей точки зрения, отношение на Х есть не что иное как произвольное подмножество U прямого произведения Х ` X. Отношение «тождество» является с этой точки зрения диагональю D Ì Х ` X, то есть множеством точек вида (х, х), х Î X. Для любого отношения U определено обратное отношение U≈1 = {(х, у); (у, х) Î U } и для любых двух отношений U и V определена их композиция U × V = {(х, у); существует z Î Х такое, что (х, z) Î U, (z, y) Î V }. Семейство отношений {U } называется (отделимой) равномерной структурой на Х (а отношения U называется окружениями диагонали), если: 1) пересечение любых двух окружений диагонали содержит окружение диагонали; 2) каждое окружение диагонали содержит D, и пересечение всех окружений диагонали совпадает с D; 3) вместе с U окружением диагонали является и U≈1; 4) для любого окружения диагонали U существует такое окружение диагонали W, что W o W Ì U. Множество, наделённое равномерной структурой, называется равномерным пространством. Отображение f: X ╝ Y равномерного пространства Х в равномерное пространство Y называется равномерно непрерывным, если прообраз при отображении f ` f: Х ` Х ╝ Y ` Y любого окружения диагонали V Ì Y ` Y содержит некоторое окружение диагонали из Х ` X. Равномерные пространства Х и Y называются равномерно гомеоморфными, если существует взаимно однозначное равномерно непрерывное отображение Х ╝ Y, обратное к которому также является равномерно непрерывным отображением. В равномерной Т. такие равномерные пространства считаются одинаковыми. Каждая равномерная структура на Х определяет некоторую структуру близости: АdВ тогда и только тогда, когда (A ` В) Ç U ¹ Æ для любого окружения диагонали U Ì X ` X. При этом равномерно непрерывные отображения оказываются близостно непрерывными. 3. Algebraische Topologie Jeder topologische Raum X (aus einer Klasse) sei mit einem algebraischen Objekt h(X) (Gruppe, Ring usw.) verknüpft und jede stetige Abbildung f: ) ╝ h(Y) (oder h(f) : h(Y) ╝ h(X), was der Identitätshomomorphismus ist, wenn f die Identitätskarte ist. Wenn h(f1 ═f2) = h(f1) ═h( f2) (bzw. h(f1 ═f2) = h(f2) h(f1), dann sagen wir, dass h ein Funktor (bzw. ein Kofunktor) ist. Die meisten Probleme in der algebraischen Theorie hängen auf die eine oder andere Weise zusammen zu folgendem Ausbreitungsproblem: Finden Sie für eine gegebene kontinuierliche Abbildung f: A ╝ Y des Unterraums A Ì X in einen topologischen Raum Y eine kontinuierliche Abbildung g: X ╝ Y, die auf A mit f zusammenfällt, d g×i, wobei i: A ╝ : h(X) ╝ h(Y) (Homomorphismus j: h(Y) ╝ h(X)), so dass h(f) = j ═h(i) (bzw. h(f) = h(i) ═j); es wird der Homomorphismus j = h(g) sein. Folglich impliziert die Nichtexistenz eines Homomorphismus j (zumindest für einen Funktor h) die Nichtexistenz der Abbildung g. Fast alle Methoden der algebraischen T können tatsächlich auf dieses einfache Prinzip reduziert werden. Beispielsweise gibt es einen Funktor h, dessen Wert auf der Kugel E n eine triviale Gruppe und auf der Kugel S n≈1 ≈ eine nichttriviale Gruppe ist, die die Kugel begrenzt . Dies impliziert bereits das Fehlen der sogenannten Retraktion ≈ kontinuierliche Abbildung ð: E n╝ S n≈1, fixiert auf S n≈1, also so, dass die Zusammensetzung ð×i, wobei i: S n-1 ╝ E n ≈ Einbettungsabbildung ist eine Identitätsabbildung (wenn p existiert, dann ist die Identitätsabbildung der Gruppe h(S n≈1) eine Zusammensetzung der Abbildungen h(i) : h(S n≈1) ╝ h (E n) und h(p) : h( E n) ╝ h(S n≈1), was für eine triviale Gruppe h(E n) unmöglich ist. Dieser im Wesentlichen elementare geometrische und (für n = 2) visuell offensichtliche Sachverhalt (physikalisch gemeint ist die Möglichkeit, eine Trommel auf einen runden Reifen zu spannen) konnte jedoch ohne den Einsatz algebraisch-topologischer Methoden bisher nicht nachgewiesen werden. Ihre unmittelbare Konsequenz ist die Aussage, dass jede stetige Abbildung f: E n╝ E n mindestens einen Fixpunkt hat, das heißt, die Gleichung f(x) = x hat mindestens eine Lösung in E n (wenn f(x) ¹ x für alle x О E n, dann sei p(x) ein Punkt aus S n≈1, kollinear zu den Punkten f(x) und x und so, dass das Segment mit den Enden f(x) und p(x ) x enthält, erhalten wir die Retraktion ð: E n╝ S n≈1). Dieser Fixpunktsatz war einer der ersten Sätze der algebraischen Theorie und wurde dann zur Quelle einer ganzen Reihe verschiedener Sätze über die Existenz von Lösungen von Gleichungen. Im Allgemeinen ist die Feststellung der Nichtexistenz eines Homomorphismus (j umso einfacher, je komplexer die algebraische Struktur von Objekten h(X) ist. Daher werden in algebraischen Theorien algebraische Objekte äußerst komplexer Natur berücksichtigt und die Anforderungen der algebraischen Die Topologie hat die Entwicklung der abstrakten Algebra erheblich stimuliert. Der topologische Raum X n Ì ¼ (die Gerüste eines Zellraums X genannt), deren Vereinigung die Gesamtheit von X ist, und die folgenden Bedingungen erfüllt sind: 1) Die Menge U Ì die Menge U Ç X n ist offen in X n; 2) X n erhält man aus 3) X0 besteht aus isolierten Punkten. Somit besteht die Struktur eines Zellraums grob gesagt darin, dass er als Vereinigung von Mengen dargestellt wird, die homöomorph zu offenen Kugeln sind (diese Mengen werden Zellen genannt). In algebraischen Techniken werden fast ausschließlich Zellräume untersucht, da die Spezifität der Probleme algebraischer Techniken für sie bereits vollständig zum Ausdruck kommt. Darüber hinaus sind tatsächlich einige besonders einfache Zellräume (wie Polyeder, siehe unten) für die algebraische Theorie von Interesse, aber die Eingrenzung der Klasse der Zellräume erschwert in der Regel das Studium erheblich (da es viele nützliche Operationen an Zellräumen gibt). abgeleitet von der Klasse der Polyeder). Zwei stetige Abbildungen f, g: = f und f1 = g (kontinuierliche Abhängigkeit von t bedeutet, dass die Formel F(x, t) = ft(x), x О X, t О eine kontinuierliche Abbildung F: X ` ╝ Y definiert; diese Abbildung sowie die Familie (ft) heißt Homotopie und verbindet f mit g). Die Menge aller stetigen Abbildungen X ╝ Y zerfällt in Homotopieklassen zueinander homotoper Abbildungen. Die Menge der Homotopieklassen stetiger Abbildungen von X nach Y wird mit dem Symbol bezeichnet. Die Untersuchung der Eigenschaften von Homotopiebeziehungen und insbesondere von Mengen ist Gegenstand der sogenannten Homotopietopologie (oder Homotopietheorie). Für die meisten interessanten topologischen Räume sind die Mengen endlich oder abzählbar und können explizit effizient berechnet werden. Topologische Räume X und Y heißen Homotopieäquivalente oder haben den gleichen Homotopietyp, wenn es stetige Abbildungen f: X ╝ Y und g: Y ╝ X gibt, so dass stetige Abbildungen g×f: ╝ Y sind homotopisch zu den entsprechenden Identitätsabbildungen. In der Homotopietheorie sollten solche Räume als identisch betrachtet werden (alle ihre „Homotopieinvarianten“ fallen zusammen). Es stellt sich heraus, dass in vielen Fällen (insbesondere für Zellräume) die Lösbarkeit des Ausbreitungsproblems nur von der Homotopieklasse der kontinuierlichen Abbildung f abhängt: A ╝ Y; Genauer gesagt, wenn für f die Verteilung g: X ╝ Y existiert, dann gibt es für jede Homotopie ft: A ╝ Y (mit f0 = f) eine Verteilung gt: Daher können wir anstelle von f seine Homotopieklasse [f] betrachten und dementsprechend nur homotopieinvariante Funktoren (Kofunktoren) h untersuchen, d. h. solche, dass h(f0) = h(f1), wenn die Abbildungen f0 und f1 sind homotopisch. Dies führt zu einer so engen Verflechtung von Algebra- und Homotopietheorie, dass sie als eine einzige Disziplin betrachtet werden können. Für jeden topologischen Raum Y definieren die Formeln h(X) = und h(f) = , wobei f: Y. Dies ist die Standardmethode (und im Wesentlichen die einzige), um homotopieinvariante Kofunktoren zu konstruieren. Damit sich herausstellt, dass die Menge h(X) beispielsweise eine Gruppe ist, muss Y entsprechend gewählt werden, um beispielsweise zu verlangen, dass es sich um eine topologische Gruppe handelt (im Allgemeinen ist dies nicht ganz richtig: es Es ist notwendig, einen Punkt x0 in Darüber hinaus reicht es aus, dass Y eine topologische Gruppe „im Sinne der Homotopie“ ist, d Homotopie.“ Solche topologischen Räume werden H-Räume genannt. Somit definiert jeder H-Raum Y einen homotopieinvarianten Kofunktor h(X) = , dessen Werte Gruppen sind. Auf ähnliche („duale“) Weise wird jeder topologische Raum Y durch die Formeln h(X) = , h(f) = definiert, wobei f: X1 ╝ X2 und j: Y ╝ X1, ein Funktor h. Damit h(X) eine Gruppe ist, muss Y eine bestimmte algebraische Struktur haben, die in einem wohldefinierten Sinne dual zur Struktur des H-Raums ist. Mit dieser Struktur ausgestattete topologische Räume werden Co-N-Räume genannt. Ein Beispiel für einen Co-H-Raum ist die n-dimensionale Kugel S n (für n ³ 1). Somit definiert für jeden topologischen Raum X die Formel pnX = eine bestimmte Gruppe pnX, n ³ 1, die als n-te Homotopiegruppe des Raums Für n > 1 ist die Gruppe pnX kommutativ. Wenn p1X= (1), dann heißt X einfach zusammenhängend. Ein Zellraum X heißt Raum K(G, n), wenn pi(X) = 0 für i ¹ n und pnX = G; Ein solcher Zellraum existiert für jedes n ³ 1 und jede Gruppe G (kommutativ für n > 1) und ist bis zur Homotopieäquivalenz eindeutig definiert. Für n > 1 (und auch für n = 1, wenn die Gruppe G kommutativ ist) erweist sich der Raum K(G, n) als H-Raum und stellt daher eine bestimmte Gruppe H n(X; G) = dar . Diese Gruppe wird als n-dimensionale Kohomologiegruppe des topologischen Raums X mit der Koeffizientengruppe G bezeichnet. Sie ist ein typischer Vertreter einer Reihe wichtiger Kofunktoren, darunter beispielsweise der K-Funktor KO(X) = [X, BO], dargestellt durch das sogenannte unendlichdimensionale Grassmannsche BO, die orientierte Cobordismusgruppe WnX usw. Wenn G ein Ring ist, dann ist die direkte Summe H*(X; G) der Gruppen H n(X; G) eine Algebra über G. Darüber hinaus hat diese direkte Summe eine sehr komplexe algebraische Struktur, in der (für G = Zp, wobei Zp ≈ zyklische Gruppe der Ordnung p) die Wirkung einer nichtkommutativen Algebra p, der sogenannten Steenrod-Algebra, auf H*(X; G) einschließt. Die Komplexität dieser Struktur ermöglicht einerseits die Entwicklung effektiver (aber keineswegs einfacher) Methoden zur Berechnung von Gruppen H n(X; G) und andererseits die Herstellung von Verbindungen zwischen den Gruppen H n( X; G) und andere homotopieinvariante Funktoren (z. B. Homotopiegruppen pnX), die es häufig ermöglichen, diese Funktoren explizit zu berechnen. Historisch gesehen gingen den Kohomologiegruppen die sogenannten Homotopiegruppen Hn(X; G) voraus, bei denen es sich um Homotopiegruppen pnM(X, G) eines Zellraums M(X, G) handelt, die eindeutig aus dem Zellraum X und dem zusammengesetzt sind Gruppe G. Homologie- und Kohomologiegruppen sind in gewissem Sinne dual zueinander und ihre Theorien sind im Wesentlichen gleichwertig. Die algebraische Struktur von Homologiegruppen ist jedoch weniger bekannt (diese Gruppen stellen beispielsweise keine Algebra, sondern eine sogenannte Kohlegebra dar), weshalb in Berechnungen üblicherweise Kohomologiegruppen verwendet werden. Gleichzeitig erweisen sich Homologiegruppen in manchen Fragestellungen als praktischer und werden daher auch untersucht. Der Teil der algebraischen Theorie, der sich mit der Untersuchung (und Anwendung) von Homologie- und Kohomologiegruppen befasst, wird Homologietheorie genannt. Die Übertragung der Ergebnisse der algebraischen Theorie auf Räume, die allgemeiner als zelluläre Räume sind, ist Gegenstand der sogenannten allgemeinen algebraischen Theorie. Insbesondere untersucht die allgemeine Homologietheorie die Homologie- und Kohomologiegruppen beliebiger topologischer Räume und ihre Anwendungen. Es zeigt sich, dass außerhalb der Klasse der kompakten zellulären Räume unterschiedliche Ansätze zur Konstruktion dieser Gruppen im Allgemeinen zu unterschiedlichen Ergebnissen führen, so dass für nichtzelluläre topologische Räume eine ganze Reihe verschiedener Homologie- und Kohomologiegruppen entsteht. Die Hauptanwendung der allgemeinen Homologietheorie liegt in der Dimensionstheorie und in der Theorie der sogenannten Dualitätsgesetze (die die Beziehung zwischen den topologischen Eigenschaften zweier zusätzlicher Teilmengen des topologischen Raums beschreiben), und ihre Entwicklung wurde maßgeblich vorangetrieben durch die Bedürfnisse dieser Theorien. 4. Stückweise lineare Topologie Eine Teilmenge Р О ═wird ein Kegel mit einem Scheitelpunkt a und einer Basis B genannt, wenn jeder ihrer Punkte zu einem einzelnen Segment der Form ab gehört, wobei b О В. Eine Teilmenge Х О ═wird ein Polyeder genannt, wenn eines davon vorhanden ist Punkte hat eine Umgebung in X, deren Abschluss ein Kegel mit kompakter Basis ist. Eine kontinuierliche Abbildung f: wird als stückweise linearer Isomorphismus bezeichnet. Gegenstand der stückweise linearen Theorie ist die Untersuchung von Polyedern und ihren stückweise linearen Abbildungen. In der stückweise linearen Theorie gelten Polyeder als identisch, wenn sie stückweise linear isomorph sind. Eine Teilmenge X О ═genau dann, wenn sie ein (kompaktes) Polyeder ist, wenn sie die Vereinigung einer (endlichen) Familie konvexer Polyeder darstellt. Jedes Polyeder kann als Vereinigung von Simplices dargestellt werden, die sich nur entlang ganzer Flächen schneiden. Diese Darstellung wird Polyeder-Triangulation genannt. Jede Triangulation wird eindeutig durch ihr Simplizialschema bestimmt, das heißt durch die Menge aller ihrer Scheitelpunkte, in denen Teilmengen markiert sind, bei denen es sich um Scheitelpunktmengen von Simplexen handelt. Daher können wir anstelle von Polyedern nur einfache Schemata ihrer Triangulationen betrachten. Mithilfe eines einfachen Schemas können beispielsweise Homologie- und Kohomologiegruppen berechnet werden. Dies geschieht wie folgt: a) Ein Simplex, dessen Eckpunkte auf eine bestimmte Weise geordnet sind, wird als geordneter Simplex einer gegebenen Triangulation (oder eines Simplizialschemas) K bezeichnet; formale lineare Kombinationen geordneter Simplices einer gegebenen Dimension n mit Koeffizienten aus einer gegebenen Gruppe G werden n-dimensionale Ketten genannt; sie alle bilden natürlicherweise eine Gruppe, die mit dem Symbol C n(K; G) bezeichnet wird; b) Entfernen des Scheitelpunkts mit der Nummer i, 0 £ i £ n, aus dem geordneten n-dimensionalen Simplex s, erhalten wir einen geordneten (n≈1)-dimensionalen Simplex, der durch das Symbol s(i) bezeichnet wird; die Kette ═ heißt Rand s; durch Linearität erweitert sich die Abbildung ═ zu einem Homomorphismus ═: Cn(K; G) ╝ Cn-1 (K; G); c) Ketten c, für die ═= 0, heißen Zyklen; sie bilden die Gruppe der Zyklen Zn(K; G); d) Ketten der Form ═ heißen Grenzen; sie bilden die Gruppe von Grenzen Bn(K; G); e) es ist bewiesen, dass Bn(K; G) М Zn(K; G) (der Rand ist ein Kreis); daher ist die Quotientengruppe Hn(K; G) = Zn(K; G)/ Bn(K; G) definiert. Es stellt sich heraus, dass die Gruppe Hn(K; G) isomorph zur Homologiegruppe Hn(X; G) des Polyeders X ist, von dem K eine Triangulation ist. Eine ähnliche Konstruktion, die nicht von Ketten, sondern von Cochains (beliebige Funktionen, die auf der Menge aller geordneten Simplexe definiert sind und Werte in G annehmen) ausgeht, ergibt Kohomologiegruppen. Mit dieser hier in leicht abgeänderter Form vorgestellten Konstruktion begann im Wesentlichen die Bildung des algebraischen T. In der ursprünglichen Konstruktion wurden die sogenannten orientierten Simplizes (Klassen geordneter Simplizes, die sich durch gerade Permutationen von Eckpunkten unterscheiden) berücksichtigt. Dieses Design wurde in den unterschiedlichsten Richtungen entwickelt und verallgemeinert. Insbesondere ihre algebraischen Aspekte führten zur sogenannten homologischen Algebra. Im allgemeinsten Sinne kann ein Simplizialschema als eine Menge definiert werden, in der bestimmte endliche Teilmengen („Simplices“) markiert sind, und es ist erforderlich, dass jede Teilmenge eines Simplex wieder ein Simplex ist. Ein solches Simplizialschema ist genau dann ein Simplizialschema für die Triangulation eines Polyeders, wenn die Anzahl der Elemente einer beliebigen markierten Teilmenge eine feste Zahl nicht überschreitet. Das Konzept eines Polyeders kann jedoch verallgemeinert werden (nachdem man die sogenannten „unendlichdimensionalen Polyeder“ erhalten hat), und dann ist jedes einfache Schema ein Schema für die Triangulation eines Polyeders (seine geometrische Realisierung genannt). Eine beliebige offene Überdeckung (Ua) jedes topologischen Raums einen nicht leeren Schnittpunkt haben. Dieses einfache Diagramm (und das entsprechende Polyeder) wird als Überdeckungsnerv bezeichnet. Die Nerven aller möglichen Hüllen nähern sich gewissermaßen dem Raum Diese Idee liegt fast allen Konstruktionen der allgemeinen Homologietheorie zugrunde. Auch im allgemeinen T spielt die Annäherung an den topologischen Raum durch die Nerven seiner offenen Hüllen eine wichtige Rolle. 5. Topologie von Mannigfaltigkeiten Ein parakompakter topologischer Raum nach Hausdorff wird als n-dimensionale topologische Mannigfaltigkeit bezeichnet, wenn er „lokal euklidisch“ ist, d. In dieser Umgebung werden Punkte durch n Zahlen x1, ┘, xn, sogenannte lokale Koordinaten, angegeben. Am Schnittpunkt zweier Karten werden die entsprechenden lokalen Koordinaten durch bestimmte Funktionen, sogenannte Übergangsfunktionen, zueinander ausgedrückt. Diese Funktionen definieren einen Homöomorphismus offener Mengen in, der als Übergangshomöomorphismus bezeichnet wird. Wir vereinbaren, einen beliebigen Homöomorphismus zwischen offenen Mengen von ═ einen t-Homöomorphismus zu nennen. Ein Homöomorphismus, der ein stückweise linearer Isomorphismus ist, wird p-Homöomorphismus genannt, und wenn er durch glatte (beliebig oft differenzierbare) Funktionen ausgedrückt wird, ≈ s-Homöomorphismus. Sei a = t, p oder s. Eine topologische Mannigfaltigkeit wird a-Mannigfaltigkeit genannt, wenn ihre Abdeckung mit Karten so gewählt ist, dass die Übergangshomöomorphismen für zwei beliebige ihrer (sich schneidenden) Karten a-Homöomorphismen sind. Eine solche Überdeckung definiert eine a-Struktur auf einer topologischen Mannigfaltigkeit X. Eine t-Mannigfaltigkeit ist also einfach jede topologische Mannigfaltigkeit; p-Mannigfaltigkeiten werden stückweise lineare Mannigfaltigkeiten genannt. Jede stückweise lineare Mannigfaltigkeit ist ein Polyeder. In der Klasse aller Polyeder zeichnen sich n-dimensionale stückweise lineare Mannigfaltigkeiten dadurch aus, dass jeder ihrer Punkte eine Nachbarschaft hat, die stückweise linear isomorph zum n-dimensionalen Würfel ist. S-Mannigfaltigkeiten werden glatte (oder differenzierbare) Mannigfaltigkeiten genannt. Eine a-Abbildung einer a-Mannigfaltigkeit heißt eine beliebige kontinuierliche Abbildung für a = t, für a = s ≈ eine beliebige stückweise lineare Abbildung, für a = s ≈ eine beliebige glatte Abbildung, also eine kontinuierliche Abbildung geschrieben in lokalen Koordinaten durch glatte Funktionen. Eine Eins-zu-Eins-a-Abbildung, deren Umkehrung ebenfalls eine a-Abbildung ist, heißt a-Homöomorphismus (für a = s auch Diffeomorphismus), a-Mannigfaltigkeiten X und Y heißen a-homöomorph (für a = s ≈ diffeomorph), wenn es existiert, obwohl es einen a-Homöomorphismus in diesem Fall gelten a-homöomorphe a-Mannigfaltigkeiten als identisch. Die Theorie der S-Varietäten ist Teil des stückweise linearen T. Die Theorie der S-Varietäten wird auch glattes T genannt. Die Hauptmethode der modernen Sortentheorie besteht darin, ihre Probleme auf Probleme algebraischer Ts zu reduzieren. für einige entsprechend konstruierte topologische Räume. Diese enge Verbindung zwischen der Varietätstheorie und der algebraischen Theorie ermöglichte einerseits die Lösung vieler schwieriger geometrischer Probleme und stimulierte andererseits die Entwicklung der algebraischen Theorie selbst stark. Beispiele für glatte Varietäten sind n- dimensionale Flächen, die keine singulären Punkte haben. Es stellt sich heraus (Einbettungssatz), dass jede glatte Mannigfaltigkeit diffeomorph zu einer solchen Oberfläche ist (für N ³ 2n + 1). Ein ähnliches Ergebnis gilt auch für a = t, p. Jede p-Varietät ist eine t-Varietät. Es stellt sich heraus, dass man auf jeder s-Mannigfaltigkeit auf natürliche Weise eine p-Struktur einführen kann (was normalerweise als Aithead-Triangulation bezeichnet wird). Wir können sagen, dass jede a-Varietät mit a = p oder s eine a▓-Varietät mit a▓ = t oder p ist. Die Antwort auf die umgekehrte Frage: Auf welche a▓-Mannigfaltigkeiten kann man eine a-Struktur einführen (eine solche a▓-Mannigfaltigkeit für a▓ = p heißt glättbar und für a▓ = t ≈trianguliert), und wenn ja, wie viele? ≈ hängt von der Dimension n ab. Es gibt nur zwei eindimensionale topologische Mannigfaltigkeiten: den Kreis S1 (kompakte Mannigfaltigkeit) und die Gerade ═ (nichtkompakte Mannigfaltigkeit). Für jedes a = p, s gibt es eine eindeutige a-Struktur auf den t-Mannigfaltigkeiten S1 und ═. In ähnlicher Weise gibt es auf jeder zweidimensionalen topologischen Mannigfaltigkeit (Oberfläche) eine eindeutige a-Struktur, und alle kompakten verbundenen Oberflächen können leicht beschrieben werden (nichtkompakte verbundene Oberflächen können ebenfalls beschrieben werden, die Antwort ist jedoch komplexer). Damit Oberflächen homöomorph sind, reicht es aus, dass sie homotopieäquivalent sind. Darüber hinaus wird der Homotopietyp jeder Oberfläche eindeutig durch ihre Homologiegruppen charakterisiert. Es gibt zwei Arten von Oberflächen: orientierbare und nicht orientierbare. Zu den Orientierungskörpern gehören die Kugel S2 und der Torus T2. Seien X und Y ≈ zwei zusammenhängende n-dimensionale a-Mannigfaltigkeiten. Schneiden wir eine Kugel in X und Y aus (für n = 2 ≈ Scheibe) und kleben wir die resultierenden Randkugeln zusammen (für n = 2 ≈ Kreis). Vorbehaltlich einiger selbstverständlicher Vorsichtsmaßnahmen ist das Ergebnis wiederum eine A-Variante. Sie wird als zusammenhängende Summe der a-Mannigfaltigkeiten X und Y bezeichnet und mit X#Y bezeichnet. T2#T2 hat beispielsweise die Form einer Brezel. Die Sphäre S n ist die Nullstelle dieser Addition, also S n # X = X für jedes X. Insbesondere ist S2 # T2 = T2. Es stellt sich heraus, dass die orientierbare Oberfläche homöomorph zu einer zusammenhängenden Summe der Form S2#T2#┘#T2 ist, die Anzahl p der Terme von T2 wird als Gattung der Oberfläche bezeichnet. Für eine Kugel gilt p = 0, für einen Torus p = 1 usw. e. Eine Oberfläche der Gattung p kann visuell als Kugel dargestellt werden, auf die p „Griffe“ geklebt sind. Jede nicht orientierbare Fläche ist homöomorph zu einer zusammenhängenden Summe P2# ¼ #P2 einer bestimmten Anzahl projektiver Ebenen P2. Man kann es sich als Kugel vorstellen, auf die mehrere Möbius-Blätter geklebt sind. Auf jeder dreidimensionalen topologischen Mannigfaltigkeit für jedes a = p, s gibt es auch eine eindeutige a-Struktur und es ist möglich, alle Homotopietypen dreidimensionaler topologischer Mannigfaltigkeiten zu beschreiben (hierfür reichen Homologiegruppen jedoch nicht mehr aus). Gleichzeitig wurden bis heute (1976) nicht alle (zumindest kompakt zusammenhängenden) dreidimensionalen topologischen Mannigfaltigkeiten eines bestimmten Homotopietyps beschrieben. Dies wurde noch nicht einmal für einfach zusammenhängende Mannigfaltigkeiten durchgeführt (sie sind alle homotopieäquivalent zur Sphäre S3). Die Poincaré-Vermutung besagt, dass jede solche Mannigfaltigkeit homöomorph zu S 3 ist. Für vierdimensionale (kompakte und zusammenhängende) topologische Mannigfaltigkeiten ist die Frage nach der Existenz und Eindeutigkeit von a-Strukturen (a = p, s) noch nicht geklärt. und ihr Homotopietyp wird nur unter der Annahme einer einfachen Verbundenheit beschrieben. Ob das Analogon der Poincaré-Vermutung für sie gilt, ist unbekannt. Bemerkenswert ist, dass sich die Situation für kompakte und zusammenhängende topologische Mannigfaltigkeiten der Dimension n ³ 5 völlig anders darstellt: Alle Hauptprobleme für sie können als prinzipiell gelöst betrachtet werden (genauer gesagt reduziert auf Probleme der algebraischen Theorie). Jede glatte Mannigfaltigkeit X kann als glatte (n-dimensionale) Oberfläche eingebettet werden; und die Tangentenvektoren an X bilden eine neue glatte Mannigfaltigkeit TX, die Tangentenbündel der glatten Mannigfaltigkeit X genannt wird. Im Allgemeinen ist ein Vektorbündel über einem topologischen Raum X ist so gegeben, dass für jeden Punkt x О X das Umkehrbild v (Schicht) ein Vektorraum ist und es eine offene Überdeckung (Ua) des Raums zum Produkt Ua ` , und es gibt einen Homöomorphismus p≈1(Ua) ╝ Ua ` , der jede Schicht p≈1(x), x О Ua, linear auf den Vektorraum (x) ` abbildet. Wenn E = TX, ordnet die kontinuierliche Abbildung p jedem Tangentenvektor den Punkt seiner Tangentialität zu, so dass die Schicht p≈1(x) der Raum ist, der X am Punkt x tangiert. Es stellt sich heraus, dass jedes Vektorbündel über einem kompakten Raum X ein Element der Gruppe KO(X) definiert. Somit ist insbesondere für jede glatte, kompakte und zusammenhängende Mannigfaltigkeit X in der Gruppe KO(X) ein Element definiert, das dem Tangentenbündel entspricht. Man nennt sie die Tangentialinvariante einer glatten Varietät X. Für jedes a gibt es ein Analogon dieser Konstruktion. Für a = p wird die Rolle der Gruppe KO(X) von einer anderen Gruppe mit der Bezeichnung KPL(X) übernommen, und für a = t wird die Rolle dieser Gruppe von einer Gruppe mit der Bezeichnung KTop(X) übernommen. Jede a-Varietät X definiert in der entsprechenden Gruppe [KO(X), KPL(X) oder KTop(X)] ein Element, das als seine a-tangentiale Invariante bezeichnet wird. Es gibt natürliche Homomorphismen KO(X) ╝ KPL(X) ╝ KTop(X), und es stellt sich heraus, dass auf einer n-dimensionalen (n ³ 5) kompakten und zusammenhängenden a"-Mannigfaltigkeit X, wobei a" = t, p , dann kann man nur dann eine a-Struktur einführen (a = p, wenn a" = t, und a = s, wenn a" = p), wenn ihre a"-tangentiale Invariante im Bild der entsprechenden Gruppe liegt. Die Anzahl der Solche Strukturen sind endlich und gleich der Anzahl der Elemente einer Quotientenmenge der Menge, wobei Ya ≈ ein speziell konstruierter topologischer Raum ist (für a = s wird der topologische Raum Ya normalerweise mit dem Symbol PL/O bezeichnet, und für a = p ≈ durch das Symbol Top/PL). Damit reduziert sich die Frage nach der Existenz und Eindeutigkeit einer a-Struktur auf ein Problem der Homotopietheorie. Der Homotopietyp des topologischen Raums PL/O ist recht kompliziert und noch nicht vollständig gelöst berechnet (1976); es ist jedoch bekannt, dass pi(PL/O) = 0 für i £ 6, was impliziert, dass jede stückweise lineare Mannigfaltigkeit der Dimension n £ 7 auf eindeutige Weise für n £ 6 glättbar ist. Auf der Im Gegenteil, der Homotopietyp des topologischen Raums Top/PL erwies sich als überraschend einfach: Dieser Raum ist homotopieäquivalent zu K(ℤ2, 3). Folglich übersteigt die Anzahl der stückweise linearen Strukturen auf einer topologischen Mannigfaltigkeit nicht die Anzahl der Elemente der Gruppe H 3(X, ℤ2). Solche Strukturen existieren sicherlich, wenn H 4(X, ℤ2) = 0, aber für H 4(X, ℤ2) ¹ 0 existiert möglicherweise keine stückweise lineare Struktur. Insbesondere gibt es eine einzigartige stückweise lineare Struktur auf der Sphäre S n. Auf der Kugel S n kann es viele glatte Strukturen geben, auf S 7 gibt es beispielsweise 28 verschiedene glatte Strukturen. Auf dem Torus T n (dem topologischen Produkt von n Kopien des Kreises S 1) existieren für n ³ 5 viele verschiedene stückweise lineare Strukturen, die alle eine glatte Struktur zulassen. Ab Dimension 5 gibt es also homöomorphe, aber keine diffeomorphen glatten Mannigfaltigkeiten; Kugeln mit dieser Eigenschaft existieren ab Dimension 7. Das Problem der Beschreibung (bis zu einem a-Homöomorphismus) aller n-dimensionalen (n ³ 5) zusammenhängenden kompakten a-Mannigfaltigkeiten kann natürlich in zwei Schritten gelöst werden: Suche nach Bedingungen für Homotopieäquivalenz von a-Mannigfaltigkeiten und Bedingungen des a-Homöomorphismus homotopieäquivalenter a-Mannigfaltigkeiten. Das erste Problem bezieht sich auf die Homotopietheorie und kann in ihrem Rahmen als vollständig gelöst betrachtet werden. Auch das zweite Problem ist im Wesentlichen vollständig gelöst (zumindest für einfach zusammenhängende a-Mannigfaltigkeiten). Grundlage seiner Lösung ist die Übertragung der Technik der „Griffzerlegung“ auf höhere Dimensionen. Mit dieser Technik ist es beispielsweise möglich, die Poincaré-Vermutung für n-dimensionale (n ³ 5) topologische Mannigfaltigkeiten (eine zusammenhängende kompakte topologische Mannigfaltigkeit, die homotopieäquivalent zu einer Kugel und homöomorph zu ihr ist) zu beweisen. Neben a-Mannigfaltigkeiten können wir auch sogenannte a-Mannigfaltigkeiten mit Rand betrachten; Sie zeichnen sich dadurch aus, dass die Umgebungen einiger ihrer Punkte (die die Kante bilden) a-homöomorph zum Halbraum Xn ³ 0 des Raumes sind. Der Rand ist eine (n≈1)-dimensionale a-Mannigfaltigkeit (im Allgemeinen unzusammenhängend). Zwei n-dimensionale kompakte a-Mannigfaltigkeiten homöomorph zu X und Y. Wenn die Einbettungsabbildungen Mithilfe von Handle-Zerlegungsmethoden lässt sich beweisen, dass für n ³ 5 einfach zusammenhängende kompakte a-Mannigfaltigkeiten a-homöomorph sind, wenn sie h-kobordant sind. Dieses h-Cobordismus-Theorem bietet die stärkste Möglichkeit, die a-Homöomorphie von a-Mannigfaltigkeiten zu beweisen (insbesondere ist die Poincaré-Vermutung eine Folge davon). Ein ähnliches, aber komplexeres Ergebnis gilt auch für nicht einfach zusammenhängende a-Mannigfaltigkeiten. Die Sammlung von ═Klassen kobordanter kompakter a-Mannigfaltigkeiten ist eine kommutative Gruppe in Bezug auf die zusammenhängende Summenoperation. Der Nullpunkt dieser Gruppe ist die Klasse der a-Mannigfaltigkeiten, die Kanten sind, also kobordant zu Null sind. Es stellt sich heraus, dass diese Gruppe für a = s isomorph zur Homotopiegruppe p2n+1MO (n+1) eines speziell konstruierten topologischen Raums MO (n+1), dem sogenannten Thom-Raum, ist. Ein ähnliches Ergebnis ergibt sich für a = p, t. Daher ermöglichen die Methoden der algebraischen Theorie grundsätzlich die Berechnung einer Gruppe. Insbesondere stellt sich heraus, dass die Gruppe ═ eine direkte Summe von Gruppen ℤ2 in einer Menge ist, die der Anzahl der Partitionen der Zahl n in andere Terme als Zahlen der Form 2m≈ entspricht
- Die Topologie ist ein Zweig der Mathematik, der das Phänomen der Kontinuität in seiner allgemeinsten Form untersucht.
- Topologie ist ein System von Mengen, das zur Definition eines topologischen Raums verwendet wird.
- Die Netzwerktopologie ist ein Diagramm des Standorts und der Verbindung von Netzwerkgeräten.
Zum Beispiel = 0 (also ist jede dreidimensionale kompakte glatte Mannigfaltigkeit eine Kante). Im Gegenteil, ═= ℤ2, es gibt also Flächen, die miteinander kobordant sind und nicht mit Null kobordant; Eine solche Fläche ist beispielsweise die projektive Ebene P
M. M. Postnikov.
6. Hauptphasen der Topologieentwicklung
Einige Ergebnisse topologischer Natur wurden bereits im 18. und 19. Jahrhundert gewonnen. (Eulers Satz über konvexe Polyeder, Klassifizierung von Oberflächen und Jordans Satz, dass eine einfache geschlossene Linie, die in einer Ebene liegt, die Ebene in zwei Teile teilt). Zu Beginn des 20. Jahrhunderts. der allgemeine Begriff des Raumes im Raum entsteht (metrisch ≈ M. Fréchet, topologisch ≈ F. Hausdorff), die ersten Ideen der Dimensionstheorie entstehen und die einfachsten Theoreme über stetige Abbildungen werden bewiesen (A. Lebesgue, L. Brouwer) , werden Polyeder eingeführt (H. Poincaré) und ihre sogenannten Betti-Zahlen bestimmt. Erstes Viertel des 20. Jahrhunderts. endet mit dem Aufblühen der allgemeinen Topologie und der Gründung der Moskauer Topologieschule; die Grundlagen der allgemeinen Dimensionstheorie werden gelegt (P. S. Uryson); die Axiomatik topologischer Räume erhält ihre moderne Form (P. S. Aleksandrov); die Theorie kompakter Räume wird aufgestellt (Alexandrov, Uryson) und der Satz über ihr Produkt bewiesen (A. N. Tikhonov); erstmals werden notwendige und hinreichende Bedingungen für die Metrisierbarkeit des Raumes gegeben (Alexandrov, Uryson); das Konzept einer lokal endlichen Überdeckung wird eingeführt (Alexandrov) [auf dessen Grundlage 1944 J. Dieudonné (Frankreich) parakompakte Räume definierte]; völlig regelmäßige Leerzeichen werden eingeführt (Tikhonov); der Begriff des Nervs wird definiert und damit die allgemeine Theorie der Homologie begründet (Alexandrow). Unter dem Einfluss von E. Noether werden Betti-Zahlen als Ränge von Homologiegruppen anerkannt, die daher auch Betti-Gruppen genannt werden. L. S. Pontryagin beweist anhand seiner Charaktertheorie die Gesetze der Dualität für geschlossene Mengen.
Im 2. Viertel des 20. Jahrhunderts. Die Entwicklung der allgemeinen Theorie und der Homologietheorie geht weiter: Bei der Entwicklung von Tikhonovs Ideen führen A. Stone (USA) und E. Cech den sogenannten Stein ≈ Tschechow oder die maximale (bi)kompakte Erweiterung eines völlig regelmäßigen Raums ein; Homologiegruppen beliebiger Räume werden definiert (Cech), Multiplikation wird in Kohomologiegruppen eingeführt (J. Alexander, A. N. Kolmogorov) und ein Kohomologiering wird konstruiert. Zu dieser Zeit herrschten in der algebraischen Theorie kombinatorische Methoden vor, die auf der Berücksichtigung einfacher Schemata beruhten; Daher wird die algebraische Theorie manchmal immer noch als kombinatorische Theorie bezeichnet. Es werden Näherungsräume und einheitliche Räume eingeführt. Die Theorie der Homotopien beginnt sich intensiv zu entwickeln (H. Hopf, Pontryagin); Homotopiegruppen werden definiert (V. Gurevich, USA) und glatte theoretische Überlegungen werden auf ihre Berechnung angewendet (Pontryagin). Die Axiome der Homologie- und Kohomologiegruppen werden formuliert (N. Steenrod und S. Eilenberg, USA). Es entsteht die Bündeltheorie (H. Whitney, USA; Pontryagin); Zellräume werden eingeführt (J. Whitehead, UK).
In der 2. Hälfte des 20. Jahrhunderts. In der UdSSR entsteht die sowjetische Schule der Allgemeinen Theorie und der Homologietheorie: Es wird an der Dimensionstheorie, dem Problem der Metrisierung, der Theorie der (bi)kompakten Erweiterungen, der allgemeinen Theorie der kontinuierlichen Abbildungen (faktorielle, offen, geschlossen), insbesondere die Theorie der Absolutheiten; Theorien sogenannter kardinalwertiger Invarianten (A.V. Arkhangelsky, B.A. Pasynkov, V.I. Ponomarev, E.G. Sklyarenko, Yu.M. Smirnov usw.).
Durch die Bemühungen einer Reihe von Wissenschaftlern (J. P. Serres und A. Cartan in Frankreich, M. M. Postnikov in der UdSSR, Whitehead usw.) wurde schließlich die Theorie der Homotopien entwickelt. Zu dieser Zeit entstanden große Zentren algebraischer Theorie in den USA, Großbritannien und anderen Ländern; Das Interesse an der geometrischen Theorie wird erneuert. Die Theorie der Vektorbündel und des K-Funktors wird geschaffen (M. Atiyah, Großbritannien; F. Hirzebruch, Deutschland), die algebraische Theorie wird häufig in der glatten Theorie verwendet (R. Thom, Frankreich) und algebraische Geometrie (Hirzebruch); Die Theorie der (Ko-)Bordismen wird entwickelt (V.A. Rokhlin, UdSSR; Tom, S.P. Novikov) und die Theorie der Glättung und Triangulierbarkeit (J. Milnor, USA).
Die Entwicklung der Technologie schreitet in alle Richtungen voran und der Anwendungsbereich erweitert sich kontinuierlich.
A. A. Maltsev.
═Ref.: Aleksandrov P.S., Einführung in die allgemeine Theorie der Mengen und Funktionen, M.≈L., 1948; Parkhomenko A. S., What is a line, M., 1954; Pontryagin L.S., Grundlagen der kombinatorischen Topologie, M.≈L., 1947; von ihm, Continuous Groups, 3. Aufl., M., 1973; Milnor J., Wallace A, Differentialtopologie. Grundkurs, trans. aus Englisch, M., 1972; Steenrod N., Chinn W., Erste Konzepte der Topologie, trans. aus Englisch, M., 1967; Aleksandrov P. S., Kombinatorische Topologie, M.≈L., 1947; Aleksandrov P. S., Pasynkov B. A., Einführung in die Dimensionstheorie. Einführung in die Theorie topologischer Räume und die allgemeine Dimensionstheorie, M., 1973; Aleksandrov P.S., Einführung in die homologische Dimensionstheorie und allgemeine kombinatorische Topologie, M., 1975; Arkhangelsky A.V., Ponomarev V.I., Grundlagen der allgemeinen Topologie in Problemen und Übungen, M., 1974; Postnikov M. M., Einführung in die Morsetheorie, M., 1971; Bourbaki N., Allgemeine Topologie. Grundstrukturen, trans. aus Französisch, M., 1968; seine, Allgemeine Topologie. Topologische Gruppen. Zahlen und verwandte Gruppen und Räume, trans. aus Französisch, M., 1969; seine, Allgemeine Topologie. Verwendung reeller Zahlen in der allgemeinen Topologie. Funktionsräume. Zusammenfassung der Ergebnisse. Wörterbuch, trans. aus Französisch, M., 1975; Kuratovsky K., Topologie, trans. aus dem Englischen, Bd. 1≈2, M., 1966≈69; Lang S., Einführung in die Theorie differenzierbarer Mannigfaltigkeiten, trans. aus Englisch, M., 1967; Spenier E., Algebraische Topologie, trans. aus Englisch, M., 1971.
Topologie (Begriffsklärung)
Topologie:
Beispiele für die Verwendung des Wortes Topologie in der Literatur.
Pontryagin, durch dessen Bemühungen ein neuer Zweig der Mathematik geschaffen wurde – die topologische Algebra –, der verschiedene algebraische Strukturen untersucht Topologie.
Und man kann Histologie ohne Hydrologie, Hydrologie ohne Geologie, Geologie ohne Geographie, Geographie ohne Topographie, Topographie ohne verstehen Topologie und alles zusammen ohne Omniologie und Omniologie – ohne Tabellen.
Wir haben die Histologie nicht verstanden. Wir haben die Hydrologie, die Hydrographie, die Geographie, die Topographie nicht verstanden. Topologie.
Im Allgemeinen beinhaltet dieser Ansatz die Dokumentation des Netzwerks Topologie, verwendete Anwendungsprogramme und Protokolle.
Also fuhr er fort und benutzte dabei immer kompliziertere Begriffe Topologie Geist und Geometrie des Bewusstseins und der Einsicht, legte die Elemente der endoskopischen Ontographie, die Klimatisierung des Gefühlslebens, seine Ebenen, Extreme, Höhen, Tiefen sowie Tiefen des Geistes dar und plauderte so lange, dass er heiser wurde, und der König hatte Kopfschmerzen.
Karten Topologie Das E-Mail-Routing eignet sich zur Lösung von Problemen bei der E-Mail-Übertragung zwischen Servern.
Ebenso hoffen wir auf eine Resolver-Bibliothek auf höherer Ebene, die Antworten basierend auf Informationen über sortiert Topologie, nur auf dem Client-Host vorhanden.
Dies bedeutet, dass das Netzwerk Topologie und Segmentierung wird zu einem wichtigen Schutzfaktor.
Schließlich kommt es im Wesentlichen bei jeder Theorie darauf an Topologie Bilder, und jede Ontologie ist nichts anderes als ein deduktiver Komplex universeller Bilder, die induktiv an die empirische Realität gebunden sind.
Erschaffen Topologie Bei Remote-Servern ermitteln Sie zunächst die Datenbanken, auf die Workstations und Server am häufigsten zugreifen.
Nämlich – in der Kontinuumswelt Topologie Seine internen Verbindungen ermöglichen es uns, eine Umgebung zu schaffen, in der Intersubjektivität zu einer Funktion der Verteilung der Rationalitäten in ihr wird.
Das heißt, so der Objektivist Topologie In der korpuskularen Welt wird das Problem der Intersubjektivität mit Hilfe eines intersubstantiellen Mittlers gelöst.
Wir reden über einige Topologien Räume fallen ineinander, verwandeln sich ineinander, so wie Buchstaben in verschiedenen Aspekten erscheinen oder sich im Monogramm eines Fensters abwechseln.
In kleinen Organisationen ist dies jedoch der Fall Topologie garantiert eine schnelle Datenaktualisierung.
Weil Sie planen Topologie, Sie sollten darüber nachdenken und Topologie E-Mail-Verkehr und Replikation.