Principiul diviziunii topologice. Topologie

Topologie- un cuvânt destul de frumos, sonor, foarte popular în unele cercuri nematematice, m-a interesat încă din clasa a IX-a. Desigur, nu aveam o idee exactă, dar bănuiam că totul era legat de geometrie.

Cuvintele și textul au fost selectate în așa fel încât totul să fie „intuitiv clar”. Rezultatul este o lipsă totală de alfabetizare matematică.

Ce este topologia ? Voi spune imediat că există cel puțin doi termeni „Topologie” - unul dintre ei pur și simplu denotă o anumită structură matematică, al doilea poartă cu el o întreagă știință. Această știință constă în studierea proprietăților unui obiect care nu se va schimba atunci când este deformat.

Exemplu ilustrativ 1. Cupa de covrigi.

Vedem că cana, prin deformări continue, se transformă într-o gogoașă (în limbajul obișnuit, un „tor bidimensional”). Sa observat că topologia studiază ceea ce rămâne neschimbat sub astfel de deformații. În acest caz, numărul de „găuri” din obiect rămâne neschimbat - există doar una. Deocamdată îl vom lăsa așa cum este, ne vom da seama puțin mai târziu)

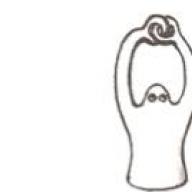
Exemplu ilustrativ 2. Omul topologic.

Prin deformări continue, o persoană (vezi poza) își poate desfășura degetele - un fapt. Nu este imediat evident, dar poți ghici. Dar dacă omul nostru topologic a avut prevederea de a pune un ceas pe o mână, atunci sarcina noastră va deveni imposibilă.

Să fim clari

Deci, sper că câteva exemple au adus o oarecare claritate la ceea ce se întâmplă.
Să încercăm să oficializăm toate acestea într-un mod copilăresc.
Vom presupune că lucrăm cu figuri de plastilină, iar plastilina poate întinderea, comprimarea, în timp ce lipirea diferitelor puncte și ruperea sunt interzise. Homeomorfe sunt figuri care se transformă unele în altele prin deformări continue descrise puțin mai devreme.

O carcasă foarte utilă este o sferă cu mânere. O sferă poate avea 0 mânere - atunci este doar o sferă, poate una - apoi este o gogoașă (în limbajul obișnuit, un „tor bidimensional”) etc.
Deci, de ce iese în evidență o sferă cu mânere printre alte figuri? Totul este foarte simplu - orice figură este homeomorfă unei sfere cu un anumit număr de mânere. Adică, în esență, nu avem nimic altceva O_o Orice obiect tridimensional este structurat ca o sferă cu un anumit număr de mânere. Fie că este o ceașcă, o lingură, o furculiță (linguriță=furculiță!), mouse de computer, persoană.

Aceasta este o teoremă destul de semnificativă care a fost demonstrată. Nu de noi și nici acum. Mai exact, s-a dovedit pentru o situație mult mai generală. Să vă explic: ne-am limitat să luăm în considerare figurile turnate din plastilină și fără cavități. Aceasta implică următoarele probleme:
1) nu putem obține o suprafață neorientabilă (sticlă Klein, bandă Möbius, plan proiectiv),
2) ne limităm la suprafețe bidimensionale (n/a: sferă - suprafață bidimensională),
3) nu putem obține suprafețe, figuri care se extind până la infinit (desigur că ne putem imagina acest lucru, dar nicio cantitate de plastilină nu va fi suficientă).

Fâșia Mobius

Sticla Klein

Termen topologie de rețea înseamnă o modalitate de a conecta computere într-o rețea. Este posibil să auziți și alte nume - structura rețelei sau Configurarea Rețelei (Este la fel). În plus, conceptul de topologie include multe reguli care determină amplasarea computerelor, metodele de așezare a cablurilor, metodele de amplasare a echipamentelor de conectare și multe altele. Până în prezent, au fost formate și stabilite mai multe topologii de bază. Dintre acestea, putem remarca „ obosi”, “inel" Și " stea”.

Topologie magistrală

Topologie obosi (sau, așa cum este adesea numit autobuz comun sau autostrada ) implică utilizarea unui singur cablu la care sunt conectate toate stațiile de lucru. Cablul comun este folosit de toate stațiile pe rând. Toate mesajele trimise de stațiile de lucru individuale sunt primite și ascultate de toate celelalte computere conectate la rețea. Din acest flux, fiecare stație de lucru selectează mesajele adresate numai acesteia.

Avantajele topologiei magistrală:

• ușurință de configurare;
• ușurință relativă de instalare și cost redus dacă toate stațiile de lucru sunt situate în apropiere;
• Eșecul uneia sau mai multor stații de lucru nu afectează în niciun fel funcționarea întregii rețele.

Dezavantajele topologiei magistralei:

• probleme cu magistrala oriunde (ruperea cablului, defectarea conectorului de rețea) duc la inoperabilitatea rețelei;
• dificultate în depanare;
• performanță scăzută – la un moment dat, un singur computer poate transmite date în rețea; pe măsură ce numărul stațiilor de lucru crește, performanța rețelei scade;
• scalabilitate slabă - pentru a adăuga noi stații de lucru este necesară înlocuirea secțiunilor magistralei existente.

Conform topologiei „autobuz” au fost construite rețelele locale cablu coaxial. În acest caz, secțiunile de cablu coaxial conectate prin conectori T au acționat ca o magistrală. Autobuzul trecea prin toate camerele și se apropia de fiecare computer. Pinul lateral al conectorului T a fost introdus în conectorul de pe placa de rețea. Cam așa arăta: Acum, astfel de rețele sunt depășite fără speranță și au fost înlocuite peste tot cu cabluri cu perechi răsucite „stea”, dar echipamentele pentru cablul coaxial pot fi încă văzute în unele întreprinderi.

Topologie inel

Inel este o topologie de rețea locală în care stațiile de lucru sunt conectate în serie între ele, formând un inel închis. Datele sunt transferate de la o stație de lucru la alta într-o direcție (într-un cerc). Fiecare PC funcționează ca un repetor, transmite mesaje către următorul computer, de exemplu. datele sunt transferate de la un computer la altul ca într-o cursă de ștafetă. Dacă un computer primește date destinate unui alt computer, le transmite mai departe de-a lungul inelului; în caz contrar, nu sunt transmise mai departe.

Avantajele topologiei inelare:

• ușurință de instalare;
• absența aproape completă a echipamentelor suplimentare;
• Posibilitatea de funcționare stabilă fără o scădere semnificativă a vitezei de transfer de date în condiții de încărcare mare a rețelei.

Cu toate acestea, „inelul” are și dezavantaje semnificative:

• fiecare stație de lucru trebuie să participe activ la transferul de informații; dacă cel puțin unul dintre ele se defectează sau se rupe cablul, funcționarea întregii rețele se oprește;
• conectarea unei noi stații de lucru necesită o oprire pe termen scurt a rețelei, deoarece inelul trebuie să fie deschis în timpul instalării unui PC nou;
• complexitatea configurarii si setarii;
• Dificultate la depanare.

Topologia de rețea în inel este folosită destul de rar. Și-a găsit aplicația principală în rețele de fibră optică Token Ring standard.

Topologie în stea

Stea este o topologie de rețea locală în care fiecare stație de lucru este conectată la un dispozitiv central (switch sau router). Dispozitivul central controlează mișcarea pachetelor în rețea. Fiecare computer este conectat printr-o placă de rețea la comutator cu un cablu separat. Dacă este necesar, puteți combina mai multe rețele împreună cu o topologie în stea - ca rezultat veți obține o configurație de rețea cu asemănător unui copac topologie. Topologia arborelui este comună în companiile mari. Nu o vom lua în considerare în detaliu în acest articol.

Topologia „stea” astăzi a devenit principala în construcția rețelelor locale. Acest lucru s-a întâmplat datorită numeroaselor sale avantaje:

• defectarea unei stații de lucru sau deteriorarea cablului acesteia nu afectează funcționarea întregii rețele;
• scalabilitate excelentă: pentru a conecta o nouă stație de lucru, trebuie doar să așezați un cablu separat de comutator;
• depanare ușoară și întreruperi ale rețelei;
• performanta ridicata;
• ușurință de configurare și administrare;
• Echipamentele suplimentare pot fi integrate cu ușurință în rețea.

Cu toate acestea, ca orice topologie, „steaua” nu este lipsită de dezavantaje:

• defectarea comutatorului central va duce la inoperabilitatea întregii rețele;
• costuri suplimentare pentru echipamentele de rețea - un dispozitiv la care vor fi conectate toate computerele din rețea (switch);
• numărul de stații de lucru este limitat de numărul de porturi din comutatorul central.

Stea – cea mai comună topologie pentru rețelele cu fir și fără fir. Un exemplu de topologie în stea este o rețea cu un cablu torsadat și un comutator ca dispozitiv central. Acestea sunt rețelele întâlnite în majoritatea organizațiilor.

Legate de.
Conţinut
Topologie generală
Topologie uniformă
Topologie algebrică
Topologie liniară pe bucăți
Topologia varietatilor
Principalele etape ale dezvoltării topologiei

1. Topologie generală
Partea de teorie care este orientată spre studiul axiomatic al continuității se numește teorie generală.Alături de algebra, teoria generală formează baza metodei moderne de teorie a mulțimilor în matematică.
Din punct de vedere axiomatic, continuitatea poate fi definită în multe moduri (în general, inegale). O axiomatică general acceptată se bazează pe conceptul unui set deschis. O structură topologică, sau topologie, pe o mulțime X este o familie de submulțimi, numite mulțimi deschise, astfel încât:
1) mulțimea goală ∅ și toate X sunt deschise;
2) uniunea oricărui număr și intersecția unui număr finit de mulțimi deschise este deschisă.
O mulțime pe care este dată o structură topologică se numește spațiu topologic. În spațiul topologic X se pot defini toate conceptele de bază ale analizei elementare legate de continuitate. De exemplu, o vecinătate a punctului x
∈ X este o mulțime deschisă arbitrară care conține acest punct; se spune că o mulțime A⊂X este închisă dacă complementul său XA este deschis; închiderea unei mulțimi A este cea mai mică mulțime închisă care conține A; dacă această închidere coincide cu X, atunci se spune că A este dens peste tot în X etc.
Prin definiție, ∅ și X sunt ambele mulțimi închise și deschise. Dacă nu există alte mulțimi în X care să fie atât închise, cât și deschise, atunci spațiul topologic X se numește conex. Un spațiu conectat vizual este format dintr-o „piesă”, în timp ce un spațiu incoerent este format din mai multe.
Orice submulțime A a unui spațiu topologic X are o structură topologică naturală constând din intersecții cu A de mulțimi deschise din X. Echipat cu această structură A se numește subspațiu al spațiului X. Fiecare spațiu metric devine topologic dacă mulțimile sale deschise sunt luate la să fie mulțimi care conțin, împreună cu un punct arbitrar, câteva vecinătăți ε ale acestuia (o bilă de rază ε centrată în acest punct). În special, orice submulțime a spațiului euclidian n-dimensional |R n este un spațiu topologic. Teoria unor astfel de spații (sub denumirea de „teoria geometrică”) și teoria spațiilor metrice sunt incluse în mod tradițional în teoria generală.
Teoria geometrică se descompune destul de clar în două părți: studiul submulților |R n de complexitate arbitrară, supuse anumitor restricții generale (un exemplu este așa-numita teorie a continuei, adică mulțimi închise mărginite conexe) și studiul a modurilor în care |R n spații topologice simple precum sferă, bilă etc. pot fi încorporate. (înglobările în |R n , de exemplu, sfere, pot fi foarte complexe).
O acoperire deschisă a unui spațiu topologic X este o familie de mulțimi deschise, a căror unire este întregul lui X. Un spațiu topologic X este numit compact (într-o altă terminologie, bicompact) dacă oricare dintre acoperirile sale deschise conține un număr finit. a elementelor care formează învelişul. Teorema clasică Heine-Borel afirmă că orice submulțime închisă mărginită |R n este compactă. Rezultă că toate teoremele de bază ale analizei elementare despre mulțimi închise mărginite (de exemplu, teorema lui Weierstrass că pe o astfel de mulțime o funcție continuă atinge valoarea maximă) sunt valabile pentru orice spații topologice compacte. Aceasta determină rolul fundamental jucat de spațiile compacte în matematica modernă (mai ales în legătură cu teoremele de existență). Identificarea clasei de spații topologice compacte a fost una dintre cele mai mari realizări ale teoriei generale, având semnificație matematică generală.
Se spune că un capac deschis (V β) este înscris într-un capac (U α) dacă pentru orice β există un α astfel încât V β ⊂ U α. Un înveliș (V β) se spune a fi local finit dacă fiecare punct x ∈ X are o vecinătate care se intersectează numai cu un număr finit de elemente ale acestui înveliș.
Se spune că un spațiu topologic este paracompact dacă orice acoperire deschisă a acestuia poate conține o acoperire finită local. Clasa spațiilor paracompacte este un exemplu de clase de spații topologice obținute prin impunerea așa-numitelor condiții de tip compactitate. Această clasă este foarte largă, în special conține toate spațiile topologice metrizabile, adică spațiile X în care poate fi introdusă o astfel de metrică
ρ că T. generat de ρ în X coincide cu T. definit în X.
Multiplicitatea unui înveliș deschis este cel mai mare număr k astfel încât există k dintre elementele sale având o intersecție nevidă. Cel mai mic număr n cu proprietatea că orice acoperire finită deschisă a unui spațiu topologic X poate conține o acoperire deschisă de multiplicitate ≤n + 1 este notat cu dimX și se numește dimensiunea lui X.
Această denumire este justificată de faptul că în situații geometrice elementare dimX coincide cu dimensiunea înțeleasă de obicei, de exemplu dim|R n = n. Sunt posibile și alte funcții numerice ale spațiului topologic X, diferite de dimX, dar în cele mai simple cazuri coincid cu dimX. Studiul lor face obiectul teoriei generale a dimensiunii - partea cea mai orientată geometric a T-ului general. Numai în cadrul acestei teorii este posibil, de exemplu, să se dea o definiție clară și destul de generală a conceptului intuitiv al unui figura geometrică și, în special, conceptul de linie, suprafață etc.
Clase importante de spații topologice se obțin prin impunerea așa-numitelor axiome de separare. Un exemplu este așa-numita axiomă Hausdorff, sau axioma T2, care necesită ca oricare două puncte distincte să aibă vecinătăți disjunse. Un spațiu topologic care satisface această axiomă se numește Hausdorff sau separabil. De ceva timp în practica matematică au fost întâlnite aproape exclusiv spații Hausdorff (de exemplu, orice spațiu metric este Hausdorff). Cu toate acestea, rolul spațiilor topologice non-Hausdorff în analiză și geometrie este în continuă creștere.
Spațiile topologice care sunt subspații ale spațiilor compacte Hausdorff (bi) se numesc complet regulate sau Tikhonov. Ele pot fi, de asemenea, caracterizate printr-o axiomă de separabilitate, și anume: o axiomă care necesită ca pentru orice punct x 0
∈ X și orice mulțime închisă F X care nu o conține, a existat o funcție continuă g: X → egală cu zero la x 0 și una pe F.
Spațiile topologice care sunt subspații deschise ale spațiilor compacte Hausdorff se numesc spații compacte local. Ele se caracterizează (în clasa spațiilor Hausdorff) prin faptul că fiecare dintre punctele lor are o vecinătate cu închidere compactă (exemplu: spațiu euclidian). Orice astfel de spațiu este completat cu un punct la unul compact (exemplu: prin adăugarea unui punct din plan se obține o sferă a unei variabile complexe, iar din |R n - o sferă S n).
O mapare f: X → Y a unui spațiu topologic X într-un spațiu topologic Y se numește mapare continuă dacă pentru orice mulțime deschisă V ⊂ Y mulțimea ƒ −1 (V) este deschisă în X. O mapare continuă se numește homeomorfism dacă este unu-la-unu și maparea inversă f − 1:Y
→ X este continuu. O astfel de mapare stabilește o corespondență unu-la-unu între mulțimi deschise de spații topologice X și Y, permutabilă cu operațiile de unire și intersecție a mulțimilor. Prin urmare, toate proprietățile topologice (adică proprietățile formulate în termeni de mulțimi deschise) ale acestor spații sunt aceleași, iar din punct de vedere topologic, spațiile topologice homeomorfe (adică spații pentru care există cel puțin un homeomorfism X → Y)
ar trebui să fie considerate identice (la fel ca în geometria euclidiană figurile care pot fi combinate prin mișcare sunt considerate identice). De exemplu, cercul și limita unui pătrat, hexagon etc. sunt homeomorfe („identice din punct de vedere topologic”). În general, oricare două linii închise simple (fără puncte duble) sunt homeomorfe. Dimpotrivă, un cerc nu este homeomorf la o dreaptă (deoarece eliminarea unui punct nu încalcă conexiunea cercului, dar încalcă conexiunea dreptei; din același motiv, o linie dreaptă nu este homeomorfă la o linie dreaptă. plan, iar un cerc nu este homeomorf la cifra opt).
De asemenea, un cerc nu este homeomorf la un plan (aruncați nu unul, ci două puncte).
Fie (X α) o familie arbitrară de spații topologice. Se consideră mulțimea X a tuturor familiilor de forma (x α ), unde x α ∈ X α (produsul direct al mulțimilor X α). Pentru orice α, formula p α ((x α )) = x α definește o mapare p α: X → X α (numită proiecție). În general vorbind, în X se pot introduce multe structuri topologice în raport cu care toate hărțile p α sunt continue.
Printre aceste structuri, există una mai mică (adică conținută în orice astfel de structură). Mulțimea X echipată cu această structură topologică se numește produsul topologic al spațiilor topologice X α și se notează cu simbolul ΠX α (și în cazul unui număr finit de factori, prin simbolul X 1 H... H X n ). În mod explicit, mulțimile deschise ale spațiului X pot fi descrise ca uniuni ale intersecțiilor finite ale tuturor mulțimilor de forma p α −1 (U α), unde U α este deschisă în X α.
Spațiul topologic X are următoarea proprietate remarcabilă a universalității, care îl caracterizează în mod unic (până la homeomorfism): pentru orice familie de hărți continue ƒ α: Y → X α există o hartă continuă unică ƒ : Y → X pentru care p α ∘ƒ=ƒ α pentru toate α. Spațiul |R n este produsul topologic al n instanțe ale dreptei numerice. Una dintre cele mai importante teoreme ale teoriei generale este afirmația că produsul topologic al spațiilor topologice compacte este compact.
Dacă X este un spațiu topologic și Y este o mulțime arbitrară și dacă i se oferă o mapare p: X → Y a spațiului X pe mulțimea Y ​​(de exemplu, dacă Y este o mulțime de câte a lui X printr-o relație de echivalență, și p este o mapare de proiecție naturală la fiecare element x ∈ X clasa sa de echivalență),
atunci putem pune problema introducerii unei structuri topologice în Y, în raport cu care maparea p este continuă. Cea mai „bogată” (în mulțimi deschise) o astfel de structură se obține considerând toate acele mulțimi V ca fiind mulțimi deschise în Y
⊂ Y pentru care mulțimea f ‑1 (V) ⊂ X este deschisă în X. Mulțimea Y ​​dotată cu această structură topologică se numește spațiu coeficient al spațiului topologic X (față de p). Are proprietatea că o hartă arbitrară ƒ : Y
→ Z este continuă dacă și numai dacă maparea ƒ∘p: X → Z este continuă O mapare continuă p: X → Y se numește factorială dacă spațiul topologic Y este, față de p, spațiul câtului spațiului topologic X. Maparea continuă p: X
→ Y se numește deschis dacă pentru orice mulțime deschisă U ⊂ X mulțimea p(U) este deschisă în Y și închis dacă pentru orice mulțime închisă F ⊂ X mulțimea p(F) este închisă în Y. Atât deschis cât și închis continuu hărți ƒ : X
→ Y, pentru care ƒ(X) = Y, sunt factoriale.
Fie X un spațiu topologic, A subspațiul său și ƒ : A → Y o hartă continuă. Presupunând că spațiile topologice X și Y sunt disjunctive, introducem X în unirea lor
∪ Y structură topologică, considerând ca mulţimi deschise uniunile mulţimilor deschise din X şi Y. În spaţiul X ∪ Y introducem cea mai mică relaţie de echivalenţă în care a ∼ ƒ(α) pentru orice punct a
∈ A. Spațiul coeficient corespunzător este notat cu X ∪ f Y și se spune că se obține prin lipirea unui spațiu topologic X de un spațiu topologic Y de-a lungul A printr-o hartă continuă ƒ. Această operație simplă și intuitivă se dovedește a fi foarte importantă, deoarece permite obținerea unora mai complexe din spații topologice relativ simple. Dacă Y este format dintr-un punct, atunci spațiul X
∪ f Y se notează cu simbolul X/A și se spune că se obține din X prin contractarea lui A la un punct. De exemplu, dacă X este un disc și A este cercul său de limită, atunci X/A este homeomorf la o sferă.
2. Topologie uniformă
Partea teoriei care studiază conceptul axiomatic al continuității se numește teorie uniformă.Definiția continuității uniforme a funcțiilor numerice, cunoscută din analiză, este direct transferată în mapările oricăror spații metrice. Prin urmare, axiomatica continuității uniforme se obține de obicei pornind de la spații metrice. Sunt explorate două abordări axiomatice ale continuității uniforme, bazate, respectiv, pe conceptele de proximitate și încercuire diagonală.
Submulțimile A și B ale unui spațiu metric X se numesc apropiate (notația AδB) dacă pentru orice ε > 0 există puncte a∈A și b∈B, distanța între care Luând proprietățile de bază ale acestei relații drept axiome, ajungem la următoarea definiție: proximitatea structurii (separabile) pe o mulțime X este o relație δ pe mulțimea tuturor submulților sale astfel încât:
1) ∅δ̅X (simbolul δ̅ denotă negația relației δ;
2)
Aδ̅B 1 şi Aδ̅B 2 ⇔ Aδ(B 1 U B 2);

3) (x) δ̅ (y) ⇔ x ≠ y;

4) dacă AδB, atunci există o mulțime Cδ̅B astfel încât Aδ(XC).
Mulțimea în care este specificată structura de proximitate se numește spațiu de proximitate. O mapare de la un spațiu de proximitate X la un spațiu de proximitate Y se spune a fi apropiată continuă dacă imaginile mulțimilor care sunt apropiate în X sunt apropiate în Y. Spațiile de proximitate X și Y sunt numite homeomorfe apropiate (sau echimorfe) dacă există o mapare continuă apropiată unu-la-unu
X → Y, inversul căruia este, de asemenea, continuu în apropiere (o astfel de mapare continuă în apropiere se numește echimorfism). În teoria uniformă, spațiile de proximitate echimorfe sunt considerate identice. Ca și spațiile metrice, orice spațiu de proximitate poate fi transformat într-un spațiu topologic (Hausdorff) luând în considerare o submulțime
U⊂X este deschis dacă (x)δ̅(XU) pentru orice punct x∈U. În acest caz, mapările continue din apropiere se dovedesc a fi mapări continue. Clasa spațiilor topologice obținute în modul descris din spații de proximitate coincide cu clasa spațiilor topologice complet regulate. Pentru orice spațiu X complet regulat, toate structurile de proximitate de pe X care generează structura sa topologică sunt în corespondență unu-la-unu cu așa-numitele compactificări (în altă terminologie, extensii bi-compacte) bX - spații topologice Hausdorff compacte care conțin X ca un spațiu dens peste tot.
Structura de proximitate δ corespunzătoare extensiei bX este caracterizată prin faptul că AδB dacă și numai dacă închiderile mulțimilor A și B se intersectează în bX. În special, pe orice spațiu topologic Hausdorff compact X există o structură unică de proximitate care generează structura sa topologică.
O altă abordare se bazează pe faptul că continuitatea uniformă într-un spațiu metric X poate fi definită prin relația „punctele x și y sunt la o distanță nu mai mare de ε”. Din punct de vedere general, o relație pe X nu este altceva decât o submulțime arbitrară U a produsului direct XХX. Relația „identitate” este, din acest punct de vedere, o diagonală Δ ⊂ X × X, adică o mulțime de puncte de forma (x, x), x∈X. Pentru orice relație U, relația inversă U −1 = ((x,y); (y,x) este definită
∈ U) și pentru oricare două relații U și V compoziția lor este definită U · V = ((x,y); există z ∈ X astfel încât (x, z) ∈ U, (z,y) ∈ V ). O familie de relații (U) se numește structură uniformă (separabilă) pe X (și relațiile U se numesc medii diagonale) dacă: 1) intersecția oricăror două medii diagonale conține un mediu diagonal; 2) fiecare mediu diagonal conţine
Δ, iar intersecția tuturor împrejurimilor diagonale coincide cu Δ; 3) împreună cu U mediul diagonalei este tot U −1 ; 4) pentru orice mediu al diagonalei U există un mediu al diagonalei W astfel încât W o W
⊂ U. O mulțime dotată cu o structură uniformă se numește spațiu uniform. O mapare ƒ : X → Y a unui spațiu uniform X într-un spațiu uniform Y se numește uniform continuă dacă imaginea inversă a mapării ƒ
Х ƒ : X Х X → Y Х Y al oricărui mediu al unei diagonale V ⊂ Y Х Y conține un mediu al unei diagonale din X Х X. Spațiile uniforme X și Y se numesc uniform homeomorfe dacă există un unu-la-unu cartografiere uniform continuă X
→ Y, inversul căruia este și o hartă uniform continuă.
În uniforma T. astfel de spații uniforme sunt considerate identice. Fiecare structură uniformă pe X definește o structură de proximitate: AδB dacă și numai dacă (A × B) ∩ U ≠ ∅ pentru orice mediu diagonal U ⊂ X × X.
În acest caz, hărțile uniform continue se dovedesc a fi aproape continue.
3. Topologie algebrică
Fie ca fiecare spatiu topologic X (din o clasa) sa fie asociat cu un obiect algebric h(X) (grup, inel, etc.), si fiecare hartie continua ƒ : X → Y sa fie asociata cu un homomorfism h(f) : h ( X)
→ h(Y) (sau h(f) : h(Y) → h(X), care este homomorfismul identităţii când ƒ este harta identităţii. Dacă h(f 1 ○ f 2) = h(f 1)
○ h(f 2) (sau, respectiv, h(f 1 ○ f 2) = h(f 2) ○ h(f 1), atunci se spune că h este un functor (respectiv, un cofunctor). Cel mai algebric T probleme.este oarecum legat de problema propagării: pentru o mapare continuă dată f: A
→ Y al unui subspațiu A ⊂ X într-un spațiu topologic Y, găsiți o mapare continuă g: X → Y care coincide pe A cu ƒ, adică astfel încât ƒ = g i, unde i: A
→ X - hartă de încorporare (i(a) = a pentru orice punct a ∈ A). Dacă o astfel de hartă continuă g există, atunci pentru orice functor (cofunctor) h există un homomorfism (φ: h(X)
→ h(Y) (homomorfism φ: h(Y) → h(X)), astfel încât h(f) = φ ○ h(i) (respectiv h(f) = h(i) ○ φ); va fi homomorfismul φ = h(g). Prin urmare, inexistența unui homomorfism
φ (pentru cel puțin un functor h) implică inexistența mapării g. Aproape toate metodele algebricei T pot fi de fapt reduse la acest principiu simplu.De exemplu, există un functor h, a cărui valoare pe minge E n este un grup trivial, iar pe sfera S n-1 care mărginește bila este un grup non-trivial. Aceasta implică deja absența așa-numitei retractări - o mapare continuă p: E n
→ S n-1 , fixat pe S n-1 , adică astfel încât compoziția p·i, unde i: S n‑1 → E n este o hartă de încorporare, este o hartă de identitate (dacă p există, atunci harta de identitate a grupului h(S n-1) va fi o compoziție de mapări h(i) : h(S n-1)
→ h(E n) și h(p) : h(E n) → h(S n-1), ceea ce este imposibil pentru grupul trivial h(E n). Cu toate acestea, acest fapt geometric elementar și (pentru n = 2) evident vizual (însemnând din punct de vedere fizic posibilitatea de a întinde un tambur pe un cerc rotund) nu a fost încă dovedit fără utilizarea metodelor algebric-topologice. Consecința sa imediată este afirmația că orice hartă continuă ƒ : E n
→ E n are cel puțin un punct fix, adică ecuația ƒ(x) = x are cel puțin o soluție în E n (dacă ƒ(x) ≠ x pentru tot x ∈ E n , atunci, luând p(x ) un punct din S n-1 coliniar la punctele ƒ(x) și x și astfel încât segmentul cu capete ƒ(x) și p(x) să conțină x, obținem retragerea p: E n
→ S n-1). Această teoremă de punct fix a fost una dintre primele teoreme ale teoriei algebrice, iar apoi a devenit sursa unei serii întregi de diverse teoreme privind existența soluțiilor ecuațiilor.
În general, cu cât structura algebrică a obiectelor h(X) este mai complexă, cu atât este mai ușor să se stabilească inexistența unui homomorfism (φ).De aceea, teoriile algebrice consideră obiectele algebrice de natură extrem de complexă, iar cerințele a topologiei algebrice a stimulat semnificativ dezvoltarea algebrei abstracte.
Un spațiu topologic X se numește spațiu celular, precum și o partiție celulară (sau complex CW), dacă conține o secvență crescătoare de subspații X 0 ⊂...
⊂ X n-1 ⊂ X n ⊂... (numite scheletele spațiului celular X), a cărui unire este întregul lui X, și sunt îndeplinite următoarele condiții: 1) mulțimea U ⊂ X este deschisă în X dacă și numai dacă pentru orice n mulțimea U
∩ X n este deschis în X n ; 2) X n se obține din X n-1 prin lipirea unei anumite familii de bile n-dimensionale de-a lungul sferelor lor (n-1)-dimensionale (prin intermediul unei mapări continue arbitrare a acestor sfere în X n-1); 3) X 0 este format din puncte izolate. Astfel, structura unui spațiu celular constă, grosier vorbind, în faptul că acesta este reprezentat ca o unire de mulțimi homeomorfe cu bile deschise (aceste mulțimi se numesc celule). În tehnicile algebrice, spațiile celulare sunt studiate aproape exclusiv, deoarece specificul problemelor tehnicilor algebrice pentru acestea este deja pe deplin manifestat. Mai mult, de fapt, unele spații celulare deosebit de simple (cum ar fi Poliedre, vezi mai jos) prezintă interes pentru sistemele algebrice, dar restrângerea clasei de spații celulare, de regulă, complică semnificativ studiul (deoarece multe operații utile asupra spațiilor celulare sunt derivate din clasa poliedrelor).
Două hărți continue f, g: X → Y se numesc homotopice dacă pot fi deformate continuu una în cealaltă, adică dacă există o familie de hărți continue f t: X → Y, continuu în funcție de parametrul t ∈ , astfel încât f 0 = ƒ și f 1 = g (dependența continuă de t înseamnă că formula F(x, t) = f t (x), x ∈ X, t
∈ definește o mapare continuă F: X Х → Y; această mapare, precum și familia (f t ) se numesc omotopie care leagă ƒ cu g). Setul tuturor mapărilor continue
X → Y se descompune în clase de homotopie de mapări homotopice între ele. Setul de clase de homotopie de mapări continue de la X la Y este notat cu simbolul . Studiul proprietăților relațiilor de homotopie și, în special, a mulțimilor este subiectul așa-numitei topologii a homotopiei (sau teoriei homotopiei). Pentru majoritatea spațiilor topologice interesante, mulțimile sunt finite sau numărabile și pot fi calculate în mod explicit eficient. Spațiile topologice X și Y se numesc echivalente de homotopie, sau având același tip de homotopie, dacă există astfel de hărți continue ƒ:
X → Y și g: Y → X astfel încât hărțile continue g·f: X → X și f·g: Y → Y sunt homotopice la hărțile de identitate corespunzătoare. În teoria homotopiei, astfel de spații ar trebui considerate identice (toți „invarianții de homotopie” lor coincid).
Rezultă că în multe cazuri (în special, pentru spațiile celulare) solubilitatea problemei de propagare depinde doar de clasa de homotopie a hărții continue ƒ : A → Y; mai precis, dacă pentru ƒ propagarea g: X
→ Y există, atunci pentru orice homotopie f t: A → Y (cu f 0 = f) există o distribuție g t: X → Y astfel încât g 0 = g. Prin urmare, în loc de ƒ, putem considera clasa sa de homotopie [f] și, în conformitate cu aceasta, studiem doar functorii (cofunctorii) invarianți de homotopie h, adică astfel încât h(f 0) = h(f 1), dacă hărţile f 0 şi f 1 homotopice. Acest lucru duce la o împletire atât de strânsă a teoriei algebrice și homotopice, încât acestea pot fi considerate ca o singură disciplină.
Pentru orice spațiu topologic Y, formulele h(X) = și h(f) = [φ○f], unde f: X 1 → X 2 și φ : X 2 → Y, definesc un cofunctor invariant de homotopie h, care este se spune că este reprezentat de spațiul topologic Y. Aceasta este o metodă standard (și în esență singura) pentru construirea cofunctorilor invarianți de homotopie. Pentru ca mulțimea h(X) să se dovedească a fi, să zicem, un grup, este necesar să se aleagă Y în consecință, de exemplu, pentru a cere ca acesta să fie un grup topologic (în general vorbind, acest lucru nu este în întregime adevărat: este este necesar să se aleagă un punct x 0 în X și să se ia în considerare numai hărți și homotopii continue, transformând x 0 într-o unitate de grup; această complicație tehnică va fi însă ignorată în cele ce urmează). Mai mult, este suficient ca Y să fie un grup topologic
„în sensul de homotopie”, adică astfel încât axiomele asociativității și existența unui element invers (care afirmă de fapt coincidența unor mapări) ar fi satisfăcute doar „până la homotopie”. Astfel de spații topologice sunt numite spații H. Astfel, fiecare H-spațiu Y definește un cofunctor invariant de homotopie h(X) = , ale cărui valori sunt grupuri.
Într-un mod similar (“dual”), fiecare spațiu topologic Y este definit prin formulele h(X) = , h(f) = [ƒ ○φ], unde ƒ : X 1
→ X 2 și φ : Y → X 1 , oarecare functor h. Pentru ca h(X) să fie un grup, Y trebuie să aibă o anumită structură algebrică, într-un sens bine definit, duală cu structura spațiului H. Spatiile topologice dotate cu aceasta structura se numesc co-N-spatii. Un exemplu de co-H-spațiu este sfera n-dimensională S n (pentru n ≥ 1).
Astfel, pentru orice spațiu topologic X, formula π n X = definește un anumit grup π n X, n ≥ 1, care se numește a n-a grupă de homotopie a spațiului X. Pentru n = 1, coincide cu grupul fundamental. Pentru n > 1 grup
π n X este comutativ. Dacă π 1 X = (1), atunci X se numește simplu conex.
Un spațiu celular X se numește spațiu K(G, n) dacă π i (X) = 0 pentru i ≠ n și π n X = G; un astfel de spațiu celular există pentru orice n ≥ 1 și orice grup G (commutativ pentru n > 1) și este determinat în mod unic până la echivalența homotopiei.
Pentru n > 1 (și de asemenea pentru n = 1, dacă grupul G este comutativ), spațiul K(G, n) se dovedește a fi un spațiu H și, prin urmare, reprezintă un anumit grup H n (X; G) = . Acest grup este numit grupul de coomologie n-dimensională a unui spațiu topologic X cu grupul de coeficienți G. Este un reprezentant tipic al unui număr de cofunctori importanți, inclusiv, de exemplu, functorul K KO(X) = , reprezentat prin așa-numitul BO Grassmannian infinit-dimensional, un grup de cobordisme orientate
Ω n X etc.
Dacă G este un inel, atunci suma directă H*(X; G) a grupurilor H n (X; G) este o algebră peste G. Mai mult, această sumă directă are o structură algebrică foarte complexă, în care (pentru G = Z p, unde Z p este un grup ciclic de ordin p) include acțiunea asupra H*(X; G) a unei algebre p necomutative, numită algebra Steenrod. Complexitatea acestei structuri permite, pe de o parte, să se dezvolte metode eficiente (dar deloc simple) de calculare a grupurilor H n (X; G) și, pe de altă parte, să se stabilească legături între grupurile H n (X). ; G) și alți functori invarianți de homotopie (de exemplu, grupuri de homotopie π n X),
care fac adesea posibilă calcularea explicită a acestor functori.
Din punct de vedere istoric, grupurile de coomologie au fost precedate de așa-numitele grupuri de omologie H n (X; G), care sunt grupuri de homotopie π n M(X, G) ale unui spațiu celular M(X, G), construite unic din spațiul celular. X și grupul G. Grupurile de omologie și coomologia într-un anumit sens sunt duale între ele, iar teoriile lor sunt în esență echivalente. Cu toate acestea, structura algebrică găsită în grupurile de omologie este mai puțin familiară (de exemplu, aceste grupuri nu constituie o algebră, ci o așa-numită coalgebră) și, prin urmare, grupurile de coomologie sunt de obicei utilizate în calcule. În același timp, în unele întrebări, grupurile de omologie se dovedesc a fi mai convenabile, așa că sunt de asemenea studiate. Partea teoriei algebrice care se ocupă cu studiul (și aplicarea) grupurilor de omologie și coomologie se numește teoria omologiei.
Transferul rezultatelor teoriei algebrice în spații mai generale decât spațiile celulare este subiectul așa-numitei teorii algebrice generale.În special, teoria omologiei generale studiază grupurile de omologie și coomologie ale spațiilor topologice arbitrare și aplicațiile acestora. Rezultă că în afara clasei de spații celulare compacte, abordări diferite ale construcției acestor grupuri conduc, în general, la rezultate diferite, astfel încât pentru spațiile topologice necelulare apar o serie întreagă de grupuri diferite de omologie și coomologie. Principala aplicație a teoriei generale a omologiei este în teoria dimensiunii și în teoria așa-numitelor legi ale dualității (care descriu relația dintre proprietățile topologice a două submulțimi suplimentare ale spațiului topologic), iar dezvoltarea acesteia a fost în mare măsură stimulată. de nevoile acestor teorii.
4. Topologie liniară pe bucăți
O submulțime P ∈ |R n se numește con cu vârful a și baza B dacă fiecare dintre punctele sale aparține unui segment unic de forma ab, unde b ∈ B. O submulțime X ∈ |R n se numește poliedru dacă există dintre punctele sale are o vecinătate în X a cărei închidere este un con cu o bază compactă. O mapare continuă ƒ : X → Y a poliedrelor se numește liniară pe bucăți dacă este liniară pe razele fiecărei vecinătăți conice a oricărui punct x ∈ X. O mapare liniară pe bucăți unu-la-unu, a cărei inversă este, de asemenea, liniară pe bucăți , se numește izomorfism liniar pe bucăți. Subiectul teoriei liniare pe bucăți este studiul poliedrelor și al mapărilor lor liniare pe bucăți. În teoria liniară pe bucăți, poliedrele sunt considerate identice dacă sunt izomorfe liniar pe bucăți.
O submulțime X ∈ |R n este un poliedru (compact) dacă și numai dacă este uniunea unei familii (finite) de poliedre convexe. Orice poliedru poate fi reprezentat ca o uniune de Simplexuri care se intersectează numai de-a lungul fețelor întregi. Această reprezentare se numește triangulație poliedrică. Fiecare triangulație este determinată în mod unic de schema sa simplială, adică de mulțimea tuturor vârfurilor sale, în care sunt marcate submulțimile, care sunt mulțimi de vârfuri de simplexuri. Prin urmare, în loc de poliedre, putem lua în considerare doar scheme simple ale triangulațiilor lor. De exemplu, folosind o schemă simplă se pot calcula grupuri de omologie și coomologie. Acest lucru se face după cum urmează:
a) un simplex ale cărui vârfuri sunt ordonate într-un anumit mod se numește simplex ordonat al unei triangulații (sau schemă simplială) dată K; combinațiile liniare formale de simplexuri ordonate de o dimensiune n dată cu coeficienți dintr-un grup dat G se numesc lanțuri n-dimensionale; toate formează în mod natural un grup, care este notat cu simbolul C n (K; G);
b) eliminând vârful cu număr i, 0 ≤ i ≤ n, din simplexul n-dimensional ordonat σ, se obține un simplex ordonat (n-1)-dimensional, care se notează cu simbolul σ (i); lanţ
∂σ = σ (0) −σ (1) + ... +(−1) n σ (n) se numește limita lui σ; prin liniaritate maparea ∂ se extinde la homomorfismul ∂ : C n (K; G) → C n-1 (K; G);
c) lanţurile c pentru care ∂c = 0 se numesc cicluri, formează un grup de cicluri Z n (K; G);
d) lanţurile de forma ∂c se numesc limite, ele constituie grupul de limite B n (K; G);
e) se demonstrează că B n (K; G) ⊂ Z n (K; G) (limita este un ciclu); prin urmare grupul de factori este definit
Hn (K; G) = Zn (K; G)/ Bn (K; G).
Se dovedește că grupul H n (K; G) este izomorf cu grupul de omologie H n (X; G) al poliedrului X, a cărui triangulare este K. O construcție similară, în care se începe nu de la lanțuri, dar din colanțuri (funcții arbitrare definite pe mulțimea tuturor simplexelor ordonate și luând valori în G), dă grupuri de coomologie.
Cu această construcție, prezentată într-o formă ușor modificată, a început, în mod esențial, formarea algebricului T. În construcția inițială au fost luate în considerare așa-numitele simplexe orientate (clase de simplexe ordonate care se disting prin permutări chiar de vârfuri). Acest design a fost dezvoltat și generalizat într-o mare varietate de direcții. În special, aspectele sale algebrice au dat naștere așa-numitei algebre omologice.
În modul cel mai general, o schemă simplială poate fi definită ca o mulțime în care sunt marcate anumite submulțimi finite („simplici”) și este necesar ca orice submulțime a unui simplex să fie din nou un simplex. O astfel de schemă simplială este o schemă simplifică pentru triangularea unui poliedru dacă și numai dacă numărul de elemente ale unei submulțimi marcate arbitrare nu depășește un număr fix. Totuși, conceptul de poliedru poate fi generalizat (obținând așa-numitele „poliedre cu dimensiuni infinite”),
și atunci orice schemă simplială va fi o schemă de triangulare a unui poliedru (numită realizarea lui geometrică).
O acoperire deschisă arbitrară (U α ) a fiecărui spațiu topologic X poate fi asociată cu o schemă simplă ale cărei vârfuri sunt elementele U α ale învelișului și o submulțime este marcată dacă și numai dacă elementele învelișului care constituie această submulțime au o intersecție negoală. Această diagramă simplă (și poliedrul corespunzător) se numește nerv de acoperire. Nervii tuturor învelișurilor posibile aproximează, într-un anumit sens, spațiul X și, pe baza grupurilor lor de omologie și coomologie, este posibil, printr-o trecere adecvată la limită, să se obțină grupele de omologie și coomologie ale lui X însuși. ideea stă la baza aproape tuturor construcțiilor teoriei generale a omologiei. Aproximarea spațiului topologic de către nervii învelișurilor sale deschise joacă, de asemenea, un rol important în general T.
5. Topologia varietatilor
Un spațiu topologic paracompact Hausdorff este numit varietate topologică n-dimensională dacă este „local euclidian”, adică dacă fiecare dintre punctele sale are o vecinătate (numită vecinătate de coordonate sau hartă) homeomorfă spațiului topologic |Rn. În această vecinătate, punctele sunt specificate prin n numere x 1,
..., x n, numite coordonate locale. La intersecția a două hărți, coordonatele locale corespunzătoare sunt exprimate una în termenii altora prin anumite funcții numite funcții de tranziție. Aceste funcții definesc un homeomorfism de mulțimi deschise în |R n și sunt numite homeomorfism de tranziție.
Să fim de acord să numim un homeomorfism arbitrar între mulțimi deschise în |R n un t-homeomorfism. Un homeomorfism care este un izomorfism liniar pe bucăți va fi numit p-homeomorfism, iar dacă este exprimat prin funcții netede (diferențiabile de orice număr de ori), îl vom numi un s-homeomorfism.
Fie α = t, p sau s. O varietate topologică se numește α-varietate dacă acoperirea sa cu hărți este aleasă astfel încât homeomorfismele de tranziție pentru oricare două dintre hărțile sale (în intersectare) să fie α-homeomorfisme. O astfel de acoperire definește o structură α pe varietatea topologică X.
Deci o varietate t este orice varietate topologică, varietățile p sunt numite varietăți liniare pe bucăți. Fiecare varietate liniară pe bucăți este un poliedru. În clasa tuturor poliedrelor, varietățile liniare în bucăți n-dimensionale sunt caracterizate prin faptul că oricare dintre punctele lor are o vecinătate izomorfă liniar în bucăți cu cubul n-dimensional. Varietățile s sunt numite varietăți netede (sau diferențiabile). O hartă α este o varietate α care se numește o mapare continuă arbitrară pentru α = t, o mapare liniară arbitrară pe bucăți pentru α = s, o mapare netedă arbitrară pentru α = s, adică o mapare continuă scrisă în coordonate locale prin funcții netede.
O hartă α unu-la-unu, a cărei inversă este și o hartă α, se numește α-homeomorfism (pentru α = s, de asemenea, un difeomorfism), α-varietățile X și Y sunt numite α-homeomorfism ( pentru α = s, difeomorf) dacă există, deși ar fi unul
α-homeomorfism X → Y.
Subiectul teoriei α-varietăților este studiul α-varietăților și α-mapările lor; în acest caz, α-varietățile α-homeomorfe sunt considerate identice. Teoria s-varietăților face parte din T liniar pe bucăți. Teoria s-varietăților se mai numește și T neted.
Metoda principală a teoriei multiplelor moderne este de a reduce problemele sale la probleme de teorie algebrică pentru anumite spații topologice construite corespunzător. Această strânsă legătură între teoria varietăților și teoria algebrică a făcut posibilă, pe de o parte, rezolvarea multor probleme geometrice dificile, iar pe de altă parte, a stimulat puternic dezvoltarea teoriei algebrice în sine.
Exemple de varietăți netede sunt suprafețele n-dimensionale din |R n care nu au puncte singulare. Se dovedește (teorema de încorporare) că orice varietate netedă este difeomorfă la o astfel de suprafață (pentru N ≥ 2n + 1). Un rezultat similar este valabil și pentru α = t, p.
Fiecare varietate p este o varietate t. Se dovedește că pe orice varietate s se poate introduce o structură p într-un mod natural (care se numește de obicei triangulație Aithead). Putem spune că orice α-varietate unde α = p sau s este o α’-varietate unde α’ = t sau p.
Răspunsul la întrebarea opusă: pe ce α’-variete putem introduce o α-structură (o astfel de α’-varietate cu α’ = p se numește netedă, iar cu α’ = t - triangulată),
si daca se poate, atunci cat? - depinde de dimensiunea n.
Există doar două varietati topologice unidimensionale: cercul S 1 (varietatea compactă) și linia dreaptă |R (varietatea necompactă). Pentru orice α = p, s există o structură α unică pe varietățile t S 1 și |R.
În mod similar, pe orice varietate (suprafață) topologică bidimensională există o structură α unică și toate suprafețele conectate compacte pot fi descrise cu ușurință (pot fi descrise și suprafețele conectate necompacte, dar răspunsul este mai complex). Pentru ca suprafețele să fie homeomorfe, este suficient ca acestea să fie echivalente cu homotopie. Mai mult, tipul de homotopie al oricărei suprafețe este caracterizat în mod unic de grupele sale de omologie. Există două tipuri de suprafețe: orientabile și neorientabile. Printre orientabile se numără sfera SI și torul TI. Fie X și Y două α-variete n-dimensionale conectate.
Să tăiem o minge în X și Y (pentru n = 2 - un disc) și să lipim sferele de limită rezultate (pentru n = 2 - cercuri). Sub rezerva unor precauții evidente, rezultatul este din nou o varietate α.
Se numește suma conexă a α-varietăților X și Y și se notează cu X#Y. De exemplu, TI#TI are forma unui covrig. Sfera S n este zero al acestei adunări, adică S n #X = X pentru orice X. În special, SІ#TI = TI. Se dovedește că suprafața orientabilă este homeomorfă la o sumă conexă de forma SІ#TI#
...#TI, numărul p de termeni TI se numește genul suprafeței. Pentru o sferă p = 0, pentru un tor p = 1 etc. O suprafață din genul p poate fi vizualizată ca o sferă de care sunt lipite p „mânere”.
Fiecare suprafață neorientabilă este homeomorfă la o sumă conexă |RPI#... #|RPI a unui anumit număr de plane proiective |RPI. Poate fi imaginat ca o sferă de care sunt lipite mai multe foi Mobius.
Pe fiecare varietate topologică tridimensională pentru orice α = p, s există, de asemenea, o structură α unică și este posibil să se descrie toate tipurile de homotopie de varietăți topologice tridimensionale (cu toate acestea, grupurile de omologie nu mai sunt suficiente pentru aceasta). În același timp, până în prezent (1976) nu au fost descrise toate (cel puțin compacte conectate) conjecturile Poincaré, este necunoscut.
Este remarcabil că pentru varietățile topologice compacte și conectate de dimensiune n ≥ 5 situația se dovedește a fi complet diferită: toate problemele principale pentru acestea pot fi considerate rezolvate în principiu (mai precis, reduse la probleme de teorie algebrică). Orice varietate netedă X este încorporată ca o suprafață netedă (n-dimensională) în IR N, iar vectorii tangenți la X constituie o nouă varietate netedă TX, care se numește mănunchiul tangent al unei varietăți netede X. În general, un pachet vectorial peste un spațiu topologic X se numește spațiu topologic E, pentru care este dată o astfel de mapare continuă
π : E → X astfel încât pentru fiecare punct x ∈ X imaginea inversă a lui v (stratul) este un spațiu vectorial și există o acoperire deschisă (U α ) a spațiului X astfel încât pentru orice α imaginea inversă
π −1 (U α) este homeomorf la produsul U α × |R n , și există un homeomorfism π −1 (U α) → U α × |R n , mapând liniar fiecare strat
π −1 (x), x ∈ U α, la spațiul vectorial (x) H |R n. Când E = TX, harta continuă π asociază fiecărui vector tangent punctul de tangență al acestuia, astfel încât stratul
π −1 (x) va fi spațiul tangent la X în punctul x. Rezultă că orice mănunchi de vectori peste un spațiu compact X definește un element al grupului KO(X). Astfel, în special, pentru orice colector X neted, compact și conectat din grupul KO(X) este definit un element corespunzător mănunchiului tangent. Se numește invariant tangențial al unei varietăți netede X. Există un analog al acestei construcții pentru orice α.
Pentru α = p, rolul grupului KO(X) este jucat de un alt grup, notat KPL(X), iar pentru α = t, rolul acestui grup este jucat de un grup notat KTop(X). Fiecare α-varietate X definește în grupul corespunzător [KO(X), KPL(X) sau KTop(X)] un element numit invariantul său α-tangențial.
Există homomorfisme naturale KO(X) → KPL(X) → KTop(X), și rezultă că pe o varietate α n-dimensională (n ≥ 5) compactă și conexă X, unde α = t, p, dacă și numai dacă se poate introduce o structură α (α = p dacă α = t, și α = s dacă α = p) când invariantul ei α-tangențial se află în imaginea grupului corespunzător.
Numărul unor astfel de structuri este finit și egal cu numărul de elemente ale unei mulțimi de factori a mulțimii, unde Y α este un spațiu topologic special construit (pentru α = s, spațiul topologic Y α este de obicei notat cu simbolul PL/ O, iar pentru α = p - prin simbolul Top/PL).
Astfel, problema existenței și unicității unei structuri α este redusă la o anumită problemă în teoria homotopiei. Tipul de homotopie a spațiului topologic PL/O este destul de complicat și nu a fost încă complet calculat (1976); se ştie totuşi că
π i (PL/O) = 0 pentru i ≤ 6, rezultă că orice varietate liniară pe bucăți de dimensiunea n ≤ 7 este netezibilă, iar pentru n ≤ 6 într-un mod unic. Dimpotrivă, tipul de homotopie al spațiului topologic Top/PL se dovedește a fi surprinzător de simplu: acest spațiu este homotopie echivalent cu K(ℤ 2 , 3).
În consecință, numărul de structuri liniare pe bucăți dintr-o varietate topologică nu depășește numărul de elemente ale grupului H i(X, ℤ 2). Astfel de structuri există cu siguranță dacă H 4 (X, ℤ 2)
= 0, dar pentru H 4 (X, ℤ 2) ≠ 0 structura liniară pe bucăți poate să nu existe.
În special, există o structură liniară unică pe bucăți pe sfera S n. Pot exista multe structuri netede pe sfera S n, de exemplu, pe S 7 există 28 de structuri netede diferite. Pe torul T n (produsul topologic al n copii ale cercului S 1) există pentru n ≥ 5 multe structuri liniare pe bucăți diferite, care admit toate o structură netedă.
Astfel, primul este echivalent cu sfera și este homeomorf cu aceasta).
Alături de α-varietăți, putem considera așa-numitele α-variete cu graniță; ele se caracterizează prin faptul că vecinătăţile unora dintre punctele lor (constituind muchia) sunt α-homeomorfe semispaţiului X n ≥ 0 al spaţiului |R n . O limită este o varietate α (n-1)-dimensională (în general vorbind, deconectată).
Se spune că două α-variete compacte n-dimensionale X și Y sunt (co)bordante dacă există o α-varietate compactă (n+1)-dimensională cu granița W, astfel încât limita sa este uniunea varietăților netede disjunse α- homeomorf la X și Y .
Dacă hărțile de încorporare X → W și Y → W sunt echivalențe de homotopie, atunci varietățile netede se numesc h-cobordante. Folosind metode de descompunere cu mâner, este posibil să se demonstreze că pentru n ≥ 5 α-variete compacte simple conectate sunt α-homeomorfe dacă sunt h-cobordante.
Această teoremă h-cobordism oferă cea mai puternică modalitate de a stabili α-homeomorfia α-varietăților (în special, conjectura Poincaré este un corolar al acesteia). Un rezultat similar, dar mai complex, este valabil și pentru α-varietățile neconectate simplu.
Colecția de n clase de α-variete compacte cobordante este un grup comutativ în raport cu operația de sumă conexă. Zeroul acestui grup este clasa α-varietăților care sunt muchii, adică cobordante cu zero. Se pare că acest grup pentru α = s este izomorf cu grupul de homotopie π 2n+1 MO (n+1) al unui spațiu topologic MO (n+1) special construit, numit spațiu Thom.
Un rezultat similar apare pentru α = p, t. Prin urmare, metodele teoriei algebrice fac posibilă, în principiu, calcularea grupului α n. În special, se dovedește că grupul s n este o sumă directă a grupurilor ℤ 2 într-o cantitate egală cu numărul de partiții ale numărului n în alți termeni decât numerele de forma 2 m -1. De exemplu, s 3 = 0 (deci fiecare varietate netedă compactă tridimensională este o limită).
Dimpotrivă, s 2 = ℤ 2, deci există suprafețe care sunt cobordante între ele și nu cobordante cu zero; o astfel de suprafață, de exemplu, este planul proiectiv |RP I.
M. M. Postnikov.
6. Principalele etape ale dezvoltării topologiei
Unele rezultate de natură topologică au fost obținute încă din secolele al XVIII-lea și al XIX-lea. (Teorema lui Euler asupra poliedrelor convexe, clasificarea suprafețelor și teorema lui Jordan că o dreaptă simplă închisă situată într-un plan împarte planul în două părți). La începutul secolului al XX-lea. se creează un concept general de spațiu în spațiu (metric - M. Fréchet, topologic - F. Hausdorff), și se construiește o prelungire (bi)compactă a unui spațiu complet regulat sub influența Elementelor; se definesc grupuri de omologie de spații arbitrare (Cech), în grupuri de coomologie (J. teoria homotopiei (H. Hopf, Pontryagin); grupurile de homotopie sunt definite (V. în Franța, M. M. Postnikov în URSS, Whitehead etc.) teoria se formează în cele din urmă homotopii.În acest moment, au fost create centre mari de topologie algebrică în SUA, și triangulabilitatea (J. Milnor, SUA).A, Topologie diferențială. Curs de început, tradus din engleză, Moscova, 1972; Steenrod N., Chinn W., Primele concepte de topologie, tradus din engleză, M., 1967; Alexandrov P. S., Combinatorial topology, M.-L., 1947; Alexandrov P. S., Pasynkov B. A., Introduction to the theory of dimension.
Introducere în teoria spațiilor topologice și teoria generală a dimensiunii, M., 1973; Aleksandrov P.S., Introducere în teoria omologică a dimensiunii și topologia combinatorie generală, M., 1975; Arkhangelsky A.V., Ponomarev V.I., Fundamentele topologiei generale în probleme și exerciții, M., 1974; Postnikov M. M., Introducere în teoria Morse, M., 1971; Bourbaki N., Topologie generală. Structuri de bază, trad. din franceză, M., 1968; lui, Topologie generală. Grupuri topologice. Numere și grupuri și spații aferente, trad. din franceză, M., 1969; lui, Topologie generală.

O rețea de calculatoare poate fi împărțită în două componente. O rețea fizică de calculatoare este, în primul rând, un echipament. Adică toate cablurile și adaptoarele necesare conectate la computere, hub-uri, comutatoare, imprimante și așa mai departe. Tot ceea ce ar trebui să funcționeze într-o rețea comună.

A doua componentă a unei rețele de calculatoare este rețeaua logică. Acesta este principiul conectării unui număr de calculatoare și a echipamentelor necesare într-un singur sistem (așa-numita topologie de rețea de calculatoare). Acest concept este mai aplicabil rețelelor locale. Este topologia selectată pentru conectarea unui număr de computere care va influența echipamentul necesar, fiabilitatea rețelei, posibilitatea de extindere a acesteia și costul lucrării. În zilele noastre, cele mai utilizate tipuri de topologii de rețele de computere sunt inel, stea și magistrală. Acesta din urmă, însă, aproape a ieșit din uz.

Steaua, inelul și magistrala sunt topologiile de bază ale rețelelor de calculatoare.

"Stea"

Topologia rețelelor de calculatoare „stea” este o structură al cărei centru este un dispozitiv de comutare. Toate computerele sunt conectate la acesta prin linii separate.

Dispozitivul de comutare poate fi un hub, adică un HUB sau un comutator. Această topologie este numită și „stea pasivă”. Dacă dispozitivul de comutare este un alt computer sau server, atunci topologia poate fi numită „stea activă”. Este dispozitivul de comutare care primește semnalul de la fiecare computer, este procesat și trimis către alte computere conectate.

Această topologie are o serie de avantaje. Avantajul incontestabil este că computerele nu depind unul de celălalt. Dacă unul dintre ele se defectează, rețeaua însăși rămâne în stare de funcționare. De asemenea, puteți conecta cu ușurință un computer nou la o astfel de rețea. Când echipamentele noi sunt conectate, elementele rămase ale rețelei vor continua să funcționeze ca de obicei. În acest tip de topologie de rețea este ușor de găsit defecțiuni. Poate că unul dintre principalele avantaje ale „stelei” este performanța sa ridicată.

Cu toate acestea, în ciuda tuturor avantajelor, acest tip de rețea de calculatoare are și dezavantaje. Dacă dispozitivul central de comutare eșuează, întreaga rețea va înceta să funcționeze. Are restricții asupra stațiilor de lucru conectate. Nu poate exista mai mult decât numărul disponibil de porturi pe dispozitivul de comutare. Iar ultimul dezavantaj al rețelei este costul acesteia. Este necesară o cantitate destul de mare de cablu pentru a conecta fiecare computer.

"Inel"

Topologia rețelelor de calculatoare „ring” nu are un centru structural. Aici, toate stațiile de lucru împreună cu serverul sunt unite într-un cerc închis. În acest sistem, semnalul se mișcă secvenţial de la dreapta la stânga într-un cerc. Toate computerele sunt repetitoare, astfel încât semnalul de marcare este menținut și transmis mai departe până ajunge la destinatar.

Acest tip de topologie are, de asemenea, atât avantaje, cât și dezavantaje. Principalul avantaj este că funcționarea rețelei de calculatoare rămâne stabilă chiar și sub sarcină grea. Acest tip de rețea este foarte ușor de instalat și necesită o cantitate minimă de echipamente suplimentare.

Spre deosebire de topologia „stea”, în topologia „ring” funcționarea întregului sistem poate fi paralizată de defecțiunea oricărui computer conectat. Mai mult, identificarea defecțiunii va fi mult mai dificilă. În ciuda instalării ușoare a acestei opțiuni de rețea, configurația sa este destul de complexă și necesită anumite abilități. Un alt dezavantaj al acestei topologii este necesitatea suspendării întregii rețele pentru a conecta echipamente noi.

"Obosi"

Topologia magistrală a rețelelor de calculatoare devine acum din ce în ce mai puțin comună. Este alcătuit dintr-o singură coloană vertebrală lungă la care sunt conectate toate computerele.

În acest sistem, ca și în altele, datele sunt trimise împreună cu adresa destinatarului. Toate computerele primesc semnalul, dar acesta este primit direct de destinatar. Stațiile de lucru conectate printr-o topologie de magistrală nu pot trimite pachete de date în același timp. În timp ce unul dintre computere efectuează această acțiune, ceilalți își așteaptă rândul. Semnalele se deplasează de-a lungul liniei în ambele direcții, dar când ajung la capăt, ele sunt reflectate și se suprapun, amenințănd buna funcționare a întregului sistem. Există dispozitive speciale - terminatoare concepute pentru a amortiza semnalele. Sunt instalate la capetele autostrăzii.

Avantajele topologiei „autobuz” includ faptul că o astfel de rețea poate fi instalată și configurată destul de rapid. În plus, instalarea acestuia va fi destul de ieftină. Dacă unul dintre computere eșuează, rețeaua va continua să funcționeze normal. Conectarea echipamentelor noi se poate face în stare de funcționare. Rețeaua va funcționa.

Dacă cablul central este deteriorat sau unul dintre terminatori nu mai funcționează, acest lucru va duce la oprirea întregii rețele. Găsirea unei defecțiuni într-o astfel de topologie este destul de dificilă. O creștere a numărului de stații de lucru reduce performanța rețelei și duce, de asemenea, la întârzieri în transferul de informații.

Topologii derivate ale rețelelor de calculatoare

Clasificarea rețelelor de calculatoare după topologie nu se limitează la trei opțiuni de bază. Există, de asemenea, tipuri de topologii precum „linie”, „inel dublu”, „topologie de plasă”, „copac”, „zăbrele”, „rețea apropiată”, „fulg de zăpadă”, „topologie complet conectată”. Toate sunt derivate din cele de bază. Să ne uităm la câteva opțiuni.

Topologii ineficiente

Într-o topologie mesh, toate stațiile de lucru sunt conectate între ele. Un astfel de sistem este destul de greoi și ineficient. Este necesar să se aloce o linie pentru fiecare pereche de computere. Această topologie este utilizată numai în sistemele cu mai multe mașini.

Topologia de plasă este, de fapt, o versiune redusă a celei complet conectate. Și aici, toate computerele sunt conectate între ele prin linii separate.

Cele mai eficiente topologii

Topologia pentru construirea rețelelor de calculatoare numită „fulg de zăpadă” este o versiune redusă a „stelei”. Aici, hub-urile conectate între ele într-un tip stea acționează ca stații de lucru. Această opțiune de topologie este considerată una dintre cele mai optime pentru rețele locale și globale mari.

De regulă, rețelele mari locale, precum și cele globale au un număr mare de subrețele construite pe diferite tipuri de topologii. Acest tip se numește mixt. Aici puteți distinge simultan „steaua”, „anvelopa” și „inelul”.

Deci, în articolul de mai sus, au fost luate în considerare toate topologiile principale de rețele de calculatoare disponibile utilizate în rețelele locale și globale, variațiile, avantajele și dezavantajele acestora.

Dicționar explicativ al limbii ruse. D.N. Uşakov

topologie

topologie, multe nu, w. (din greaca topos - loc si logos - invatatura) (mat.). Parte a geometriei care studiază proprietățile calitative ale figurilor (adică, independent de concepte precum lungimea, unghiurile, dreptatea etc.).

Noul dicționar explicativ al limbii ruse, T. F. Efremova.

topologie

și. O ramură a matematicii care studiază proprietățile calitative ale figurilor geometrice, independent de lungimea lor, unghiuri, dreptate etc.

Dicţionar enciclopedic, 1998

topologie

TOPOLOGIA (din greaca topos - loc si... logica) este o ramura a matematicii care studiaza proprietatile topologice ale figurilor, i.e. proprietăți care nu se modifică sub nicio deformație produsă fără ruperi și lipire (mai precis, cu mapări one-to-one și continue). Exemple de proprietăți topologice ale figurilor sunt dimensiunea, numărul de curbe care mărginesc o zonă dată etc. Astfel, un cerc, o elipsă și conturul unui pătrat au aceleași proprietăți topologice, deoarece aceste linii pot fi deformate una în alta în modul descris mai sus; în același timp, inelul și cercul au proprietăți topologice diferite: cercul este limitat de un contur, iar inelul de două.

Topologie

(din grecescul topos ≈ loc și ¼ logie) ≈ parte a geometriei dedicată studiului fenomenului de continuitate (exprimat, de exemplu, în conceptul de limită). Varietatea manifestărilor de continuitate în matematică și o gamă largă de abordări diferite ale studiului acesteia au condus la dezintegrarea matematicii unificate într-un număr de departamente („matematică generală”, „matematică algebrică” etc.), care diferă unele de altele în subiectul și metoda de studiu și de fapt foarte puțin legate între ele. I. Topologie generală Partea de teorie care este orientată spre studiul axiomatic al continuității se numește teorie generală.Alături de algebra, teoria generală formează baza metodei moderne de teorie a mulțimilor în matematică. Din punct de vedere axiomatic, continuitatea poate fi definită în multe moduri (în general, inegale). O axiomatică general acceptată se bazează pe conceptul unui set deschis. O structură topologică, sau topologie, pe o mulțime X este o familie de submulțimi ale sale, numite mulțimi deschise, astfel încât: 1) mulțimea goală Æ și tot X sunt deschise; 2) uniunea oricărui număr și intersecția unui număr finit de mulțimi deschise este deschisă. O mulțime pe care este dată o structură topologică se numește spațiu topologic. În spațiul topologic X se pot defini toate conceptele de bază ale analizei elementare legate de continuitate. De exemplu, o vecinătate a unui punct x О X este o mulțime deschisă arbitrară care conține acest punct; o mulţime A Ì X se numeşte închisă dacă complementul ei X \ A este deschis; închiderea unei mulțimi A este cea mai mică mulțime închisă care conține A; dacă această închidere coincide cu X, atunci se spune că A este dens peste tot în X etc. Prin definiție, Æ și X sunt ambele mulțimi închise și deschise. Dacă nu există alte mulțimi în X care să fie atât închise, cât și deschise, atunci spațiul topologic X se numește conex. Un spațiu conectat vizual este format dintr-o „piesă”, în timp ce un spațiu deconectat este format din mai multe. Orice submulțime A a unui spațiu topologic X are o structură topologică naturală constând din intersecții cu A de mulțimi deschise din X. Echipat cu această structură A se numește subspațiu al spațiului X. Fiecare spațiu metric devine topologic dacă mulțimile sale deschise sunt luate la să fie mulțimi care conțin, împreună cu un punct arbitrar, unele e-vecinătate (o bilă de rază e centrată în acest punct). În special, orice submulțime a unui spațiu euclidian n-dimensional ═este un spațiu topologic. Teoria unor astfel de spații (sub denumirea de „teoria geometrică”) și teoria spațiilor metrice sunt în mod tradițional incluse în teoria generală.Teoria geometrică este destul de clar împărțită în două părți: studiul submulților de complexitate arbitrară, sub rezerva anumitor restricții de o natură generală (un exemplu este așa-numita teorie a continue, adică mulțimi închise mărginite conectate) și studiul modalităților în care spații topologice simple precum o sferă, o bilă etc. pot fi încorporate în ═. (investițiile în, de exemplu, sfere pot fi foarte complexe). O acoperire deschisă a unui spațiu topologic X este o familie de mulțimi deschise, a căror unire este întregul lui X. Un spațiu topologic X este numit compact (în altă terminologie, bicompact) dacă oricare dintre acoperirile sale deschise conține un număr finit. de elemente care formează şi învelişul. Teorema clasică Heine ≈ Borel afirmă că orice submulțime închisă mărginită este ═compact. Rezultă că toate teoremele de bază ale analizei elementare despre mulțimi închise mărginite (de exemplu, teorema lui Weierstrass că pe o astfel de mulțime o funcție continuă atinge valoarea maximă) sunt valabile pentru orice spații topologice compacte. Aceasta determină rolul fundamental jucat de spațiile compacte în matematica modernă (mai ales în legătură cu teoremele de existență). Identificarea clasei de spații topologice compacte a fost una dintre cele mai mari realizări ale teoriei generale, având semnificație matematică generală. Se spune că un capac deschis (Vb) este înscris într-un capac (Ua) dacă pentru oricare b există un a astfel încât Vb Ì Ua. Un înveliș (Vb) se numește local finit dacă fiecare punct x Î X are o vecinătate care se intersectează numai cu un număr finit de elemente ale acestui înveliș. Se spune că un spațiu topologic este paracompact dacă orice acoperire deschisă a acestuia poate conține o acoperire finită local. Clasa spațiilor paracompacte este un exemplu de clase de spații topologice obținute prin impunerea așa-numitelor condiții de tip compactitate. Această clasă este foarte largă, în special, conține toate spațiile topologice metrizabile, adică spațiile X în care este posibil să se introducă o metrică r astfel încât T generat de r în X să coincidă cu T definit în X. Multiplicitatea a unui înveliș deschis este cel mai mare, numărul k este astfel încât există k dintre elementele sale având o intersecție nevidă. Cel mai mic număr n, care are proprietatea că un înveliș deschis cu multiplicitatea £n + 1 poate fi înscris în orice înveliș finit deschis al unui spațiu topologic X, este notat cu simbolul dimX și se numește dimensiunea lui X. Acest nume este justificată de faptul că în situații geometrice elementare dimX coincide cu dimensiunea uzuală de înțeles, de exemplu dim = n. Sunt posibile și alte funcții numerice ale spațiului topologic X, diferite de dimX, dar în cele mai simple cazuri coincid cu dimX. Studiul lor este subiectul teoriei generale a dimensiunii, partea cea mai orientată geometric a T generalului. Numai în cadrul acestei teorii este posibil, de exemplu, să se dea o definiție clară și destul de generală a conceptului intuitiv al unei figuri geometrice și, în special, a conceptului de linie, suprafață etc. Clase importante de spații topologice se obțin prin impunerea așa-numitelor axiome de separare. Un exemplu este așa-numita axiomă Hausdorff, sau axioma T2, care necesită ca oricare două puncte distincte să aibă vecinătăți disjunse. Un spațiu topologic care satisface această axiomă se numește Hausdorff sau separabil. De ceva timp în practica matematică au fost întâlnite aproape exclusiv spații Hausdorff (de exemplu, orice spațiu metric este Hausdorff). Cu toate acestea, rolul spațiilor topologice non-Hausdorff în analiză și geometrie este în continuă creștere. Spațiile topologice care sunt subspații ale spațiilor compacte Hausdorff (bi) se numesc complet regulate sau Tikhonov. Ele pot fi, de asemenea, caracterizate printr-o axiomă de separabilitate, și anume: o axiomă care necesită ca pentru orice punct x0 ═X și orice mulțime închisă F ═X care nu o conține, să existe o funcție continuă g: X ╝ egală cu zero la x0 și unu pe F. Spațiile topologice care sunt subspații deschise ale spațiilor compacte Hausdorff se numesc local spații compacte. Ele se caracterizează (în clasa spațiilor Hausdorff) prin faptul că fiecare dintre punctele lor are o vecinătate cu închidere compactă (exemplu: spațiu euclidian). Orice astfel de spațiu este completat cu un punct la unul compact (exemplu: prin adăugarea unui punct din plan se obține o sferă a unei variabile complexe, iar din ═≈ o sferă S n). O mapare f: X ╝ Y dintr-un spațiu topologic X într-un spațiu topologic Y se numește mapare continuă dacă pentru orice mulțime deschisă V М Y mulțimea f≈1(V) este deschisă în X. O mapare continuă se numește homeomorfism dacă este unu-la-unu și maparea inversă f≈ 1: Y ╝ X continuă. O astfel de mapare stabilește o corespondență unu-la-unu între mulțimi deschise de spații topologice X și Y, permutabilă cu operațiile de unire și intersecție a mulțimilor. Prin urmare, toate proprietățile topologice (adică proprietățile formulate în termeni de mulțimi deschise) ale acestor spații sunt aceleași, iar din punct de vedere topologic, spațiile topologice homeomorfe (adică spații pentru care există cel puțin un homeomorfism X ╝ Y) ar trebui să fie considerate la fel (la fel ca în geometria euclidiană, figurile care pot fi combinate prin mișcare sunt considerate identice). De exemplu, cercul și limita unui pătrat, hexagon etc. sunt homeomorfe („identice din punct de vedere topologic”). În general, oricare două linii închise simple (fără puncte duble) sunt homeomorfe. Dimpotrivă, un cerc nu este homeomorf la o dreaptă (deoarece eliminarea unui punct nu încalcă conexiunea cercului, dar încalcă conexiunea dreptei; din același motiv, o linie dreaptă nu este homeomorfă la o linie dreaptă. plan, iar un cerc nu este homeomorf la cifra opt). De asemenea, un cerc nu este homeomorf la un plan (aruncați nu unul, ci două puncte). Fie (Xa) ≈ o ​​familie arbitrară de spații topologice. Se consideră mulțimea X a tuturor familiilor de forma (xa), unde xa ═Xa (produsul direct al mulțimilor Xa). Pentru orice a, formula definește o mapare ═ (numită proiecție). În general vorbind, în X se pot introduce multe structuri topologice în raport cu care toate hărțile pa sunt continue. Printre aceste structuri, există una mai mică (adică conținută în orice astfel de structură). Mulțimea X echipată cu această structură topologică se numește produsul topologic al spațiilor topologice Xa și se notează cu simbolul PHa (și în cazul unui număr finit de factori, prin simbolul X1 ` ... ` Xn). În mod explicit, mulțimile deschise ale spațiului X pot fi descrise ca uniuni de intersecții finite ale tuturor mulțimilor de forma în care Ua este deschisă în Xa. Spațiul topologic X are următoarea proprietate remarcabilă de universalitate, care îl caracterizează în mod unic (până la homeomorfism): pentru orice familie de mapări continue fa: Y ╝ Xa există o mapare continuă unică f: Y ╝ X pentru care ══pentru toate A. Spațiul ═este produsul topologic al n instanțe ale dreptei numerice. Una dintre cele mai importante teoreme ale teoriei generale este afirmația că produsul topologic al spațiilor topologice compacte este compact. Dacă X ≈ spațiu topologic și Y ≈ o mulțime arbitrară și dacă este dată o mapare p: X ╝ Y a spațiului X pe mulțimea Y ​​(de exemplu, dacă Y este o mulțime de coeficient de X printr-o relație de echivalență, și p este o mapare de proiecție naturală la fiecare element x Î X este clasa sa de echivalență), atunci putem pune problema introducerii în Y a unei structuri topologice în raport cu care maparea p este continuă. Cea mai „bogată” (în mulțimi deschise) o astfel de structură se obține considerând ca mulțimi deschise în Y toate acele mulțimi V Ì Y pentru care mulțimea f‑1(V) Ì X este deschisă în X. Mulțimea Y ​​echipată cu aceasta structura topologică se numește spațiul coeficient al spațiului topologic X (față de p). Are proprietatea că o mapare arbitrară f: Y ╝ Z este continuă dacă și numai dacă maparea ═: X ╝ Z este continuă O mapare continuă p: X ╝ Y se numește factor dacă spațiul topologic Y este un spațiu factorial al spațiul topologic față de p X. O mapare continuă p: X ╝ Y se numește deschisă dacă pentru orice mulțime deschisă U Ì X mulțimea p(U) este deschisă în Y și închisă dacă pentru orice mulțime închisă F Ì X mulţimea p(F) este închisă în Y. Cât de deschise şi închise hărţile continue f: X ╝ Y pentru care f(X) = Y sunt factoriale. Fie X ≈ un spațiu topologic, A ≈ subspațiul său și f: A ╝ Y ≈ o hartă continuă. Presupunând că spațiile topologice X și Y sunt disjunctive, introducem o structură topologică în uniunea lor X È Y, considerând uniunile de mulțimi deschise din X și Y ca fiind mulțimi deschise. În continuare, introducem în spațiul X È Y cea mai mică echivalență. relație în care a ~ f(a) pentru orice punct a Î A. Spațiul coeficient corespunzător este notat cu simbolul X È fY și se spune că se obține prin lipirea spațiului topologic X de spațiul topologic Y de-a lungul lui A prin mijlocul unei hărți continue f. Această operație simplă și intuitivă se dovedește a fi foarte importantă, deoarece permite obținerea unora mai complexe din spații topologice relativ simple. Dacă Y este format dintr-un punct, atunci spațiul X È fY este notat cu simbolul X/A și se spune că se obține din X prin contractarea lui A la un punct. De exemplu, dacă X ≈ un disc și A ≈ cercul său de limită, atunci X/A este homeomorf la o sferă. 2. Topologie uniformă Partea teoriei care studiază conceptul axiomatic de continuitate uniformă se numește teorie uniformă.Definiția continuității uniforme a funcțiilor numerice, cunoscută din analiză, este transferată direct în mapările oricăror spații metrice. Prin urmare, axiomatica continuității uniforme se obține de obicei pornind de la spații metrice. Două abordări axiomatice ale continuității uniforme, bazate, respectiv, pe conceptele de proximitate și încercuire diagonală, sunt explorate în detaliu. Submulțimile A și B ale spațiului metric X se numesc apropiate (notația AdB) dacă pentru orice e > 0 există puncte a Î A și b Î B, distanța dintre care< e. Принимая основные свойства этого отношения за аксиомы, приходят к следующему определению: (отделимой) структурой близости на множестве Х называется такое отношение d на множестве всех его подмножеств, что: 1) ÆX (символом обозначается отрицание отношения d; 2) AB1 и AB2Û A(B1 U B2); ═3) {x}{y} Û x ¹ y;4) если АВ, то существует такое множество С В, что А(Х\С). Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости Х в пространство близости Y называется близостно непрерывным, если образы близких в Х множеств близки в Y. Пространства близости Х и Y называются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение X ╝ Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Т. эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество u Ì x открытым, если {x}(X \U) для любой точки х Î U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства Х все структуры близости на X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии ≈ би-компактными расширениями) вХ ≈ компактными хаусдорфовыми топологическими пространствами, содержащими Х в качестве всюду плотного пространства. Структура близости d, соответствующая расширению вХ, характеризуется тем, что АdВ тогда и только тогда, когда замыкания множеств А и В пересекаются в bX. В частности, на любом компактном хаусдорфовом топологическом пространстве Х существует единственная структура близости, порождающая его топологическую структуру. Другой подход основан на том, что равномерную непрерывность в метрическом пространстве Х можно определить в терминах отношения «точки х и у находятся на расстоянии, не большем e». С общей точки зрения, отношение на Х есть не что иное как произвольное подмножество U прямого произведения Х ` X. Отношение «тождество» является с этой точки зрения диагональю D Ì Х ` X, то есть множеством точек вида (х, х), х Î X. Для любого отношения U определено обратное отношение U≈1 = {(х, у); (у, х) Î U } и для любых двух отношений U и V определена их композиция U × V = {(х, у); существует z Î Х такое, что (х, z) Î U, (z, y) Î V }. Семейство отношений {U } называется (отделимой) равномерной структурой на Х (а отношения U называется окружениями диагонали), если: 1) пересечение любых двух окружений диагонали содержит окружение диагонали; 2) каждое окружение диагонали содержит D, и пересечение всех окружений диагонали совпадает с D; 3) вместе с U окружением диагонали является и U≈1; 4) для любого окружения диагонали U существует такое окружение диагонали W, что W o W Ì U. Множество, наделённое равномерной структурой, называется равномерным пространством. Отображение f: X ╝ Y равномерного пространства Х в равномерное пространство Y называется равномерно непрерывным, если прообраз при отображении f ` f: Х ` Х ╝ Y ` Y любого окружения диагонали V Ì Y ` Y содержит некоторое окружение диагонали из Х ` X. Равномерные пространства Х и Y называются равномерно гомеоморфными, если существует взаимно однозначное равномерно непрерывное отображение Х ╝ Y, обратное к которому также является равномерно непрерывным отображением. В равномерной Т. такие равномерные пространства считаются одинаковыми. Каждая равномерная структура на Х определяет некоторую структуру близости: АdВ тогда и только тогда, когда (A ` В) Ç U ¹ Æ для любого окружения диагонали U Ì X ` X. При этом равномерно непрерывные отображения оказываются близостно непрерывными. 3. Topologie algebrică Fie fiecare spațiu topologic X (din o clasă) să fie asociat cu un obiect algebric h(X) (grup, inel etc.), și fie fiecare hartă continuă f: X ╝ Y ≈ un homomorfism h(f) : h( X ) ╝ h(Y) (sau h(f) : h(Y) ╝ h(X), care este homomorfismul identităţii când f este harta identităţii. Dacă h(f1 ═f2) = h(f1) ═h( f2) (sau, respectiv, h(f1 ═f2) = h(f2) h(f1), atunci spunem că h este un functor (respectiv, un cofunctor). Majoritatea problemelor din teoria algebrică sunt într-un fel sau altul legate la următoarea problemă de propagare: pentru o mapare continuă dată f: A ╝ Y a subspațiului A Ì X într-un spațiu topologic Y, găsiți o mapare continuă g: X ╝ Y care coincide pe A cu f, adică astfel încât f = g×i, unde i: A ╝ X ≈ înglobare mapare (i(a) = a pentru orice punct a О A). Dacă o astfel de mapare continuă g există, atunci pentru orice functor (cofunctor) h există un homomorfism (j : h(X) ╝ h(Y) (homomorfism j: h(Y) ╝ h(X)), astfel încât h(f) = j ═h(i) (respectiv, h(f) = h(i) ═j); va fi homomorfismul j = h(g). În consecință, inexistența unui homomorfism j (cel puțin pentru un functor h) implică inexistența mapării g. Aproape toate metodele algebricei T pot fi de fapt reduse la acest principiu simplu.De exemplu, există un functor h a cărui valoare pe minge E n este un grup trivial, iar pe sfera S n≈1 ≈ un grup netrivial care mărginește bila. . Aceasta implică deja absența așa-numitei retrageri ≈ mapare continuă р: E n╝ S n≈1, fixată pe S n≈1, adică astfel încât compoziția р×i, unde i: S n‑1 ╝ E n ≈ embedding mapping , este o mapare de identitate (dacă p există, atunci maparea de identitate a grupului h(S n≈1) va fi o compoziție a mapărilor h(i) : h(S n≈1) ╝ h (E n) și h(p) : h( E n) ╝ h(S n≈1), ceea ce este imposibil pentru un grup trivial h(E n). Cu toate acestea, acest fapt geometric elementar și (pentru n = 2) evident vizual (însemnând din punct de vedere fizic posibilitatea de a întinde un tambur pe un cerc rotund) nu a fost încă dovedit fără utilizarea metodelor algebric-topologice. Consecința sa imediată este afirmația că orice mapare continuă f: E n╝ E n are cel puțin un punct fix, adică ecuația f(x) = x are cel puțin o soluție în E n (dacă f(x) ¹ x pentru toate x О E n, atunci, luând p(x) un punct din S n≈1, coliniar cu punctele f(x) și x și astfel încât segmentul cu capete f(x) și p(x) ) conţine x, obţinem retragerea р: E n╝ S n≈1). Această teoremă de punct fix a fost una dintre primele teoreme ale teoriei algebrice, iar apoi a devenit sursa unei serii întregi de diverse teoreme privind existența soluțiilor ecuațiilor. În general, stabilirea inexistenței unui homomorfism (j este mai ușoară, cu cât structura algebrică a obiectelor h(X) este mai complexă. Prin urmare, în teoriile algebrice sunt luate în considerare obiectele algebrice de natură extrem de complexă, iar cerințele algebricei. topologia a stimulat semnificativ dezvoltarea algebrei abstracte.Spațiul topologic X se numește spațiu celular, precum și partiție celulară (sau complex CW), dacă conține o succesiune crescândă de subspații X 0 М ¼ М X n≈1 М X n М ¼ (numite scheletele unui spațiu celular X), a cărui unire este întregul lui X și sunt îndeplinite următoarele condiții: 1) mulțimea U Ì X este deschisă în X dacă și numai dacă pentru orice n mulţimea U Ç X n este deschisă în X n; 2) X n se obține din X n≈1 prin lipirea unei anumite familii de bile n-dimensionale de-a lungul sferelor lor (n≈1)-dimensionale (prin intermediul unei mapări continue arbitrare a acestor sfere la X n≈1); 3) X0 este format din puncte izolate. Astfel, structura unui spațiu celular constă, grosier vorbind, în faptul că acesta este reprezentat ca o unire de mulțimi homeomorfe cu bile deschise (aceste mulțimi se numesc celule). În tehnicile algebrice, spațiile celulare sunt studiate aproape exclusiv, deoarece specificul problemelor tehnicilor algebrice pentru acestea este deja pe deplin manifestat. Mai mult, de fapt, unele spații celulare deosebit de simple (cum ar fi poliedre, vezi mai jos) sunt de interes pentru teoria algebrică, dar restrângerea clasei de spații celulare, de regulă, complică semnificativ studiul (deoarece multe operații utile asupra spațiilor celulare sunt derivate din clasa poliedrelor). Două hărți continue f, g: X ╝ Y sunt numite homotopice dacă pot fi deformate continuu una în cealaltă, adică dacă există o familie de hărți continue ft: X ╝ Y care depind continuu de parametrul t О astfel încât f0 = f și f1 = g (dependența continuă de t înseamnă că formula F(x, t) = ft(x), x О X, t О definește o hartă continuă F: X ` ╝ Y; această hartă, precum și familia (ft) se numește omotopie, legând f la g). Setul tuturor mapărilor continue X ╝ Y se împarte în clase de homotopie de mapări homotopice între ele. Setul de clase de homotopie de mapări continue de la X la Y este notat cu simbolul . Studiul proprietăților relațiilor de homotopie și, în special, a mulțimilor este subiectul așa-numitei topologii a homotopiei (sau teoriei homotopiei). Pentru majoritatea spațiilor topologice interesante, mulțimile sunt finite sau numărabile și pot fi calculate în mod explicit eficient. Spațiile topologice X și Y se numesc echivalente de homotopie, sau având același tip de homotopie, dacă există hărți continue f: X ╝ Y și g: Y ╝ X astfel încât hărțile continue g×f: X ╝ X și f×g: Y ╝ Y sunt homotopice la mapările de identitate corespunzătoare. În teoria homotopiei, astfel de spații ar trebui considerate identice (toți „invarianții de homotopie” lor coincid). Rezultă că în multe cazuri (în special, pentru spațiile celulare) solubilitatea problemei de propagare depinde doar de clasa de homotopie a mapării continue f: A ╝ Y; mai precis, dacă pentru f există distribuția g: X ╝ Y, atunci pentru orice homotopie ft: A ╝ Y (cu f0 = f) există o distribuție gt: X ╝ Y astfel încât g0 = g. Prin urmare, în loc de f, putem considera clasa sa de homotopie [f] și, în conformitate cu aceasta, studiem doar functorii (cofunctorii) invarianți de homotopie h, adică astfel încât h(f0) = h(f1) dacă hărțile f0 și f1 sunt homotopice. Acest lucru duce la o împletire atât de strânsă a teoriei algebrice și homotopice, încât acestea pot fi considerate ca o singură disciplină. Pentru orice spațiu topologic Y, formulele h(X) = și h(f) = , unde f: X1 ╝ X2 și j: X2 ╝ Y, definesc un cofunctor invariant de homotopie h, despre care se spune că este reprezentat de spațiul topologic Y. Această ≈ metodă standard (și în esență singura) pentru construirea cofunctorilor invarianți de homotopie. Pentru ca mulțimea h(X) să se dovedească a fi, să zicem, un grup, este necesar să se aleagă Y în consecință, de exemplu, pentru a cere ca acesta să fie un grup topologic (în general vorbind, acest lucru nu este în întregime adevărat: este este necesar să se aleagă un punct x0 în X și să se ia în considerare numai hărți și homotopii continue, transformând x0 în unitatea grupului; această complicație tehnică va fi însă ignorată în cele ce urmează). Mai mult, este suficient ca Y să fie un grup topologic „în sensul de homotopie”, adică axiomele asociativității și existența unui element invers (care afirmă de fapt coincidența anumitor hărți) să fie satisfăcute doar „până la homotopie.” Astfel de spații topologice sunt numite spații H. Astfel, fiecare H-spațiu Y definește un cofunctor invariant de homotopie h(X) = , ale cărui valori sunt grupuri. Într-un mod similar (“dual”), fiecare spațiu topologic Y este definit prin formulele h(X) = , h(f) = , unde f: X1 ╝ X2 și j: Y ╝ X1, un functor h. Pentru ca h(X) să fie un grup, Y trebuie să aibă o anumită structură algebrică, într-un sens bine definit, duală cu structura spațiului H. Spatiile topologice dotate cu aceasta structura se numesc co-N-spatii. Un exemplu de co-H-spațiu este sfera n-dimensională S n (pentru n ³ 1). Astfel, pentru orice spațiu topologic X, formula pnX = definește un anumit grup pnX, n ³ 1, care se numește a n-a grupă de homotopie a spațiului X. Pentru n = 1, coincide cu grupul fundamental. Pentru n > 1 grupul pnX este comutativ. Dacă p1X= (1), atunci X se numește simplu conex. Un spațiu celular X se numește spațiu K(G, n) dacă pi(X) = 0 pentru i ¹ n și pnX = G; un astfel de spațiu celular există pentru orice n ³ 1 și orice grup G (commutativ pentru n > 1) și este definit în mod unic până la echivalența homotopiei. Pentru n > 1 (și, de asemenea, pentru n = 1, dacă grupul G este comutativ), spațiul K(G, n) se dovedește a fi un spațiu H și, prin urmare, reprezintă un anumit grup H n(X; G) = . Acest grup este numit grupul de coomologie n-dimensional al spațiului topologic X cu grupul de coeficienți G. Este un reprezentant tipic al unui număr de cofunctori importanți, inclusiv, de exemplu, functorul K KO(X) = [X, BO], reprezentat de așa-numitul BO Grassmanian infinit-dimensional, grupul de cobordism orientat WnX etc. Dacă G este un inel, atunci suma directă H*(X; G) a grupurilor H n(X; G) este o algebră peste G. Mai mult, această sumă directă are o structură algebrică foarte complexă, în care (pentru G = Zp, unde Zp ≈ grup ciclic de ordin p) include acțiunea asupra H*(X; G) a unei algebre p necomutative, numită algebra Steenrod. Complexitatea acestei structuri permite, pe de o parte, să se dezvolte metode eficiente (dar deloc simple) pentru calcularea grupelor H n(X; G), și, pe de altă parte, să se stabilească legături între grupurile H n( X; G) și alți functori invarianți de homotopie (de exemplu, grupuri de homotopie pnX), care fac adesea posibilă calcularea explicită a acestor functori. Din punct de vedere istoric, grupurile de coomologie au fost precedate de așa-numitele grupuri de omologie Hn(X; G), care sunt grupuri de homotopie pnM(X, G) ale unui spațiu celular M(X, G), construite unic din spațiul celular X și grupa G. Grupurile de omologie și coomologie sunt într-un anumit sens duale între ele, iar teoriile lor sunt în esență echivalente. Cu toate acestea, structura algebrică găsită în grupurile de omologie este mai puțin familiară (de exemplu, aceste grupuri nu constituie o algebră, ci o așa-numită coalgebră) și, prin urmare, grupurile de coomologie sunt de obicei utilizate în calcule. În același timp, în unele întrebări, grupurile de omologie se dovedesc a fi mai convenabile, așa că sunt de asemenea studiate. Partea teoriei algebrice care se ocupă cu studiul (și aplicarea) grupurilor de omologie și coomologie se numește teoria omologiei. Transferul rezultatelor teoriei algebrice în spații mai generale decât spațiile celulare este subiectul așa-numitei teorii algebrice generale.În special, teoria omologiei generale studiază grupurile de omologie și coomologie ale spațiilor topologice arbitrare și aplicațiile acestora. Rezultă că în afara clasei de spații celulare compacte, abordări diferite ale construcției acestor grupuri conduc, în general, la rezultate diferite, astfel încât pentru spațiile topologice necelulare apar o serie întreagă de grupuri diferite de omologie și coomologie. Principala aplicație a teoriei generale a omologiei este în teoria dimensiunii și în teoria așa-numitelor legi ale dualității (care descriu relația dintre proprietățile topologice a două submulțimi suplimentare ale spațiului topologic), iar dezvoltarea acesteia a fost în mare măsură stimulată. de nevoile acestor teorii. 4. Topologie liniară pe bucăți O submulțime Р О ═ se numește con cu un vârf a și o bază B dacă fiecare dintre punctele sale aparține unui singur segment de forma ab, unde b О В. O submulțime Х О ═ se numește poliedru dacă oricare dintre ele. puncte are o vecinătate în X, a cărei închidere este un con cu o bază compactă. O mapare continuă f: X ╝ Y a poliedrelor se numește liniară pe bucăți dacă este liniară pe razele fiecărei vecinătăți conice a oricărui punct x О X. O mapare liniară pe bucăți unu-la-unu, a cărei inversă este, de asemenea, liniară pe bucăți , se numește izomorfism liniar pe bucăți. Subiectul teoriei liniare pe bucăți este studiul poliedrelor și al mapărilor lor liniare pe bucăți. În teoria liniară pe bucăți, poliedrele sunt considerate identice dacă sunt izomorfe liniar pe bucăți. O submulțime X О ═dacă și numai dacă este un poliedru (compact) dacă reprezintă unirea unei familii (finite) de poliedre convexe. Orice poliedru poate fi reprezentat ca o uniune de simplexe care se intersectează numai de-a lungul fețelor întregi. Această reprezentare se numește triangulație poliedrică. Fiecare triangulație este determinată în mod unic de schema sa simplială, adică de mulțimea tuturor vârfurilor sale, în care sunt marcate submulțimile, care sunt mulțimi de vârfuri de simplexuri. Prin urmare, în loc de poliedre, putem lua în considerare doar scheme simple ale triangulațiilor lor. De exemplu, folosind o schemă simplă se pot calcula grupuri de omologie și coomologie. Aceasta se face astfel: a) un simplex ale cărui vârfuri sunt ordonate într-un anumit fel se numește simplex ordonat al unei triangulații (sau schemă simplială) dată K; combinațiile liniare formale de simplexuri ordonate de o dimensiune n dată cu coeficienți dintr-un grup dat G se numesc lanțuri n-dimensionale; toate formează în mod natural un grup, care este notat cu simbolul C n(K; G); b) eliminând vârful cu numărul i, 0 £ i £ n, din simplexul n-dimensional ordonat s, obținem un simplex (n≈1)-dimensional ordonat, care se notează cu simbolul s(i); lanțul ═ se numește limita s; prin liniaritate maparea ═ se extinde la un homomorfism ═: Cn(K; G) ╝ Cn-1 (K; G); c) lanţurile c pentru care ═= 0 se numesc cicluri, constituie grupul de cicluri Zn(K; G); d) lanţurile de forma ═ se numesc limite, ele constituie grupul de limite Bn(K; G); e) se demonstrează că Bn(K; G) М Zn(K; G) (limita este un ciclu); prin urmare, grupa de coeficient Hn(K; G) = Zn(K; G)/Bn(K; G) este definită. Rezultă că grupul Hn(K; G) este izomorf cu grupul de omologie Hn(X; G) al poliedrului X, din care K este o triangulație. O construcție similară, care pornește nu de la lanțuri, ci de la colanțuri (funcții arbitrare definite pe mulțimea tuturor simplexurilor ordonate și luând valori în G), dă grupuri de coomologie. Cu această construcție, prezentată aici într-o formă ușor modificată, a început în mod esențial formarea algebricului T. În construcția inițială au fost luate în considerare așa-numitele simplexuri orientate (clase de simplexuri ordonate care se disting prin permutări pare ale vârfurilor). Acest design a fost dezvoltat și generalizat într-o mare varietate de direcții. În special, aspectele sale algebrice au dat naștere așa-numitei algebre omologice. În modul cel mai general, o schemă simplială poate fi definită ca o mulțime în care sunt marcate anumite submulțimi finite („simplici”) și este necesar ca orice submulțime a unui simplex să fie din nou un simplex. O astfel de schemă simplială este o schemă simplifică pentru triangularea unui poliedru dacă și numai dacă numărul de elemente ale unei submulțimi marcate arbitrare nu depășește un număr fix. Totuși, conceptul de poliedru poate fi generalizat (obținând așa-numitele „poliedre cu dimensiuni infinite”), și atunci orice schemă simplială va fi o schemă pentru triangularea unui poliedru (numită realizarea lui geometrică). O acoperire arbitrară deschisă (Ua) a fiecărui spațiu topologic X poate fi asociată cu o schemă simplă, ale cărei vârfuri sunt elementele Ua ale acoperirii și o submulțime este marcată dacă și numai dacă elementele învelișului care constituie această submulțime au o intersecție negoală. Această diagramă simplă (și poliedrul corespunzător) se numește nerv de acoperire. Nervii tuturor învelișurilor posibile aproximează, într-un anumit sens, spațiul X și, pe baza grupurilor lor de omologie și coomologie, este posibil, printr-o trecere adecvată la limită, să se obțină grupele de omologie și coomologie ale lui X însuși. ideea stă la baza aproape tuturor construcțiilor teoriei generale a omologiei. Aproximarea spațiului topologic de către nervii învelișurilor sale deschise joacă, de asemenea, un rol important în general T. 5. Topologia varietatilor Un spațiu topologic paracompact Hausdorff este numit o varietate topologică n-dimensională dacă este „local euclidian”, adică dacă fiecare dintre punctele sale are o vecinătate (numită vecinătate de coordonate sau hartă) homeomorfă spațiului topologic. În această vecinătate, punctele sunt specificate prin n numere x1, ┘, xn, numite coordonate locale. La intersecția a două hărți, coordonatele locale corespunzătoare sunt exprimate una în termenii altora prin anumite funcții numite funcții de tranziție. Aceste funcții definesc un homeomorfism de mulțimi deschise în, numit homeomorfism de tranziție. Să fim de acord să numim un homeomorfism arbitrar între mulțimi deschise de ═ un t-homeomorfism. Un homeomorfism care este un izomorfism liniar pe bucăți va fi numit p-homeomorfism, iar dacă este exprimat prin funcții netede (diferențiabile de orice număr de ori), ≈ s-homeomorfism. Fie a = t, p sau s. O varietate topologică este numită a-varietate dacă acoperirea sa cu hărți este aleasă astfel încât homeomorfismele de tranziție pentru oricare două dintre hărțile sale (în intersectare) sunt a-homeomorfisme. O astfel de acoperire definește o structură a pe o varietate topologică X. Astfel, o varietate t este pur și simplu orice varietate topologică, varietățile p sunt numite varietăți liniare pe bucăți. Fiecare varietate liniară pe bucăți este un poliedru. În clasa tuturor poliedrelor, varietățile liniare în bucăți n-dimensionale sunt caracterizate prin faptul că oricare dintre punctele lor are o vecinătate izomorfă liniar în bucăți cu cubul n-dimensional. Varietățile s sunt numite varietăți netede (sau diferențiabile). o mapare a o varietate a se numește o mapare continuă arbitrară pentru a = t, pentru a = s ≈ o mapare liniară arbitrară pe bucăți, pentru a = s ≈ o mapare netedă arbitrară, adică o mapare continuă scrisă în coordonate locale prin funcții netede. O hartă a unu-la-unu, a cărei inversă este și o hartă a, se numește a-homeomorfism (pentru a = s și difeomorfism), a-varietățile X și Y sunt numite a-homeomorfism (pentru a = s ≈ difeomorf) dacă există deși ar exista un a-homeomorfism X ╝ Y. Subiectul teoriei a-varietăților este studiul a-varietăților și a-hărților lor; în acest caz, a-varietățile a-homeomorfe sunt considerate identice. Teoria soiurilor s face parte din T liniar pe bucăți. Teoria soiurilor s se mai numește și T neted. Metoda principală a teoriei varietăților moderne este de a reduce problemele sale la probleme de T algebric. pentru unele spații topologice construite corespunzător. Această legătură strânsă între teoria varietăților și teoria algebrică a făcut posibilă, pe de o parte, rezolvarea multor probleme geometrice dificile și, pe de altă parte, a stimulat puternic dezvoltarea teoriei algebrice în sine.Exemple de varietăți netede sunt n- suprafeţe dimensionale care nu au puncte singulare. Se dovedește (teorema de încorporare) că orice varietate netedă este difeomorfă la o astfel de suprafață (pentru N ³ 2n + 1). Un rezultat similar este valabil și pentru a = t, p. Fiecare varietate p este o varietate t. Se dovedește că pe orice varietate s se poate introduce o structură p într-un mod natural (care se numește de obicei triangulație Aithead). Putem spune că orice a-varietate unde a = p sau s este o a▓-varietate unde a▓ = t sau p. Răspunsul la întrebarea opusă: pe care a▓-variete se poate introduce o structură a (o astfel de a▓-varietate pentru a▓ = p se numește netezibilă, iar pentru a▓ = t ≈triangulată), iar dacă da, câți? ≈ depinde de dimensiunea n. Există doar două varietati topologice unidimensionale: cercul S1 (varietatea compactă) și linia dreaptă ═ (varietatea necompactă). Pentru orice a = p, s există o structură a unică pe t-varietățile S1 și ═. În mod similar, pe orice varietate (suprafață) topologică bidimensională există o structură a unică și toate suprafețele conectate compacte pot fi descrise cu ușurință (pot fi descrise și suprafețele conectate necompacte, dar răspunsul este mai complex). Pentru ca suprafețele să fie homeomorfe, este suficient ca acestea să fie echivalente cu homotopie. Mai mult, tipul de homotopie al oricărei suprafețe este caracterizat în mod unic de grupele sale de omologie. Există două tipuri de suprafețe: orientabile și neorientabile. Printre orientabile se numără sfera S2 și torul T2. Fie X și Y ≈ două varietati a n-dimensionale conectate. Să tăiem o minge în X și Y (pentru n = 2 ≈ disc) și să lipim sferele de limită rezultate (pentru n = 2 ≈ cerc). Sub rezerva unor precauții evidente, rezultatul este din nou o varietate. Se numește o sumă conexă a a-varietăților X și Y și se notează cu X#Y. De exemplu, T2#T2 are forma unui covrig. Sfera S n este zero al acestei adunări, adică S n # X = X pentru orice X. În special, S2 # T2 = T2. Se dovedește că suprafața orientabilă este homeomorfă la o sumă conexă de forma S2#T2#┘#T2, numărul p de termeni ai lui T2 se numește genul suprafeței. Pentru o sferă p = 0, pentru un tor p = 1 etc. e. O suprafață din genul p poate fi reprezentată vizual ca o sferă de care sunt lipite p „mânere”. Fiecare suprafață neorientabilă este homeomorfă la o sumă conexă P2# ¼ #P2 a unui anumit număr de planuri proiective P2. Poate fi imaginat ca o sferă de care sunt lipite mai multe foi Mobius. Pe fiecare varietate topologică tridimensională pentru orice a = p, s există, de asemenea, o structură a unică și este posibil să se descrie toate tipurile de homotopie de varietăți topologice tridimensionale (cu toate acestea, grupurile de omologie nu mai sunt suficiente pentru aceasta). În același timp, până în prezent (1976) nu au fost descrise toate varietățile topologice tridimensionale (cel puțin compacte conectate) de un anumit tip de homotopie. Acest lucru nu s-a făcut nici măcar pentru varietati pur și simplu conectate (toate sunt echivalente homotopie cu sfera S3). Conjectura Poincaré afirmă că orice astfel de varietate este homeomorfă pentru S 3. Pentru varietăți topologice cu patru dimensiuni (compacte și conectate), problema existenței și unicității structurilor a (a = p, s) nu a fost încă rezolvată, iar tipul lor de homotopie este descris numai sub ipoteza unei simple conexiuni. Nu se știe dacă analogul conjecturii Poincaré este valabil pentru ei. Este remarcabil că pentru varietăți topologice compacte și conectate de dimensiunea n ³ 5 situația se dovedește a fi complet diferită: toate problemele principale pentru acestea pot fi considerate rezolvate în principiu (mai precis, reduse la probleme de teorie algebrică). Orice colector neted X poate fi încorporat ca o suprafață netedă (n-dimensională) în; iar vectorii tangenți la X constituie o nouă varietate netedă TX, care se numește mănunchiul tangent al varietății netede X. În general, un pachet vectorial peste un spațiu topologic X este un spațiu topologic E pentru care o mapare continuă p: E ╝ X este dat astfel încât pentru fiecare punct x О X imaginea inversă v (stratul) este un spațiu vectorial și există o acoperire deschisă (Ua) a spațiului X astfel încât pentru orice a imaginea inversă p≈1(Ua) este homeomorfă la produsul Ua ` , și există un homeomorfism p≈1(Ua) ╝ Ua ` , mapând liniar fiecare strat p≈1(x), x О Ua, pe spațiul vectorial (x) ` . Când E = TX, maparea continuă p asociază cu fiecare vector tangent punctul său de tangență, astfel încât stratul p≈1(x) va fi tangenta spațiului la X în punctul x. Rezultă că orice mănunchi de vectori peste un spațiu compact X definește un element al grupului KO(X). Astfel, în special, pentru orice colector X neted, compact și conectat din grupul KO(X) este definit un element corespunzător mănunchiului tangent. Se numește invariant tangențial al unui soi neted X. Există un analog al acestei construcții pentru orice a. Pentru a = p, rolul grupului KO(X) este jucat de un alt grup, notat KPL(X), iar pentru a = t, rolul acestui grup este jucat de un grup notat KTop(X). Fiecare a-varietate X definește în grupul corespunzător [KO(X), KPL(X) sau KTop(X)] un element numit invariantul său a-tangențial. Există homomorfisme naturale KO(X) ╝ KPL(X) ╝ KTop(X), și se dovedește că pe un n-dimensional (n ³ 5) compact și conectat a"-varietate X, unde a" = t, p , atunci numai atunci se poate introduce o structură a (a = p dacă a" = t și a = s dacă a" = p) când invariantul său a"-tangențial se află în imaginea grupului corespunzător. astfel de structuri este finită și egală cu numărul de elemente ale unei mulțimi de câte a mulțimii, unde Ya ≈ un spațiu topologic special construit (pentru a = s, spațiul topologic Ya este de obicei notat cu simbolul PL/O, iar pentru a = p ≈ prin simbolul Top/PL).Astfel, problema existenței și unicității structurii a- se reduce la o problemă în teoria homotopiei.Tipul de homotopie a spațiului topologic PL/O este destul de complicat și nu a fost încă complet calculat (1976); cu toate acestea, se știe că pi(PL/O) = 0 pentru i £ 6, ceea ce implică faptul că orice varietate liniară pe bucăți de dimensiunea n £ 7 este netezibilă într-un mod unic pentru n £ 6. dimpotrivă, tipul de homotopie al spațiului topologic Top/PL s-a dovedit a fi surprinzător de simplu: acest spațiu este homotopie echivalent cu K(ℤ2, 3). În consecință, numărul de structuri liniare pe bucăți dintr-o varietate topologică nu depășește numărul de elemente ale grupului H 3(X, ℤ2). Astfel de structuri există cu siguranță dacă H 4(X, ℤ2) = 0, dar pentru H 4(X, ℤ2) ¹ 0 este posibil să nu existe o structură liniară pe bucăți. În special, există o structură liniară unică pe bucăți pe sfera S n. Pot exista multe structuri netede pe sfera S n, de exemplu, pe S 7 există 28 de structuri netede diferite. Pe torul T n (produsul topologic al n copii ale cercului S 1) există pentru n ³ 5 multe structuri liniare pe bucăți diferite, care admit toate o structură netedă. Astfel, începând de la dimensiunea 5, există varietăți netede homeomorfe, dar nu difeomorfe; sfere cu această proprietate există pornind de la dimensiunea 7. Problema descrierii (până la un a-homeomorfism) a tuturor n-dimensionale (n ³ 5) a-varietăți compacte conectate poate fi rezolvată în mod natural în două etape: căutați condiții pentru echivalența homotopiei de a-varietăți și condiții a-homeomorfism de homotopie a-varietăți echivalente. Prima problemă se referă la teoria homotopiei și în cadrul acesteia poate fi considerată complet rezolvată. A doua problemă este, de asemenea, în esență complet rezolvată (cel puțin pentru a-varietățile simple conectate). Baza soluției sale este transferul tehnicii de „descompunere a mânerului” la dimensiuni mai mari. Folosind această tehnică, este posibil, de exemplu, să se demonstreze conjectura Poincaré pentru varietăți topologice n-dimensionale (n ³ 5) (o varietate topologică compactă conectată care este echivalentă homotopie cu o sferă și este homeomorfă cu aceasta). Alături de a-varietățile, putem considera așa-numitele a-varietăți cu graniță; ele se caracterizează prin faptul că vecinătățile unora dintre punctele lor (constituind muchia) sunt a-homeomorfe semispațiului Xn ³ 0 al spațiului. Granița este o varietate a (n≈1)-dimensională (în general vorbind, deconectată). Două varietati a compacte n-dimensionale X și Y se spune că sunt (co)bordante dacă există o varietate a compactă (n+1)-dimensională cu granița W, astfel încât granița sa este uniunea unor varietăți netede disjunse a- homeomorf la X și Y Dacă mapările de încorporare X ╝ W și Y ╝ W sunt echivalențe homotopie, atunci varietățile netede sunt numite h-cobordante. Folosind metode de descompunere cu mâner, este posibil să se demonstreze că pentru n ³ 5 a-varietățile compacte pur și simplu conectate sunt a-homeomorfe dacă sunt h-cobordante. Această teoremă h-cobordism oferă cea mai puternică modalitate de a stabili homeomorfia a-varietăților a (în special, conjectura Poincaré este un corolar al acesteia). Un rezultat similar, dar mai complex, este valabil și pentru varietatile a neconectate simplu. Colecția de ═clase de a-variete compacte cobordante este un grup comutativ în raport cu operația de sumă conexă. Zeroul acestui grup este clasa a-varietăților care sunt muchii, adică cobordante cu zero. Se pare că acest grup pentru a = s este izomorf cu grupul de homotopie p2n+1MO (n+1) al unui spațiu topologic MO (n+1) special construit, numit spațiu Thom. Un rezultat similar are loc pentru a = p, t. Prin urmare, metodele teoriei algebrice fac posibilă, în principiu, calcularea unui grup. În special, se dovedește că grupul ═este o sumă directă a grupurilor ℤ2 într-o sumă egală cu numărul de partiții ale numărului n în alți termeni decât numerele de forma 2m≈

De exemplu, = 0 (deci fiecare colector neted compact tridimensional este o muchie). Dimpotrivă, ═= ℤ2, deci există suprafețe care sunt cobordante între ele și nu cobordante cu zero; o astfel de suprafață, de exemplu, este planul proiectiv P

M. M. Postnikov.

6. Principalele etape ale dezvoltării topologiei

Unele rezultate de natură topologică au fost obținute încă din secolele al XVIII-lea și al XIX-lea. (Teorema lui Euler asupra poliedrelor convexe, clasificarea suprafețelor și teorema lui Jordan că o dreaptă simplă închisă situată într-un plan împarte planul în două părți). La începutul secolului al XX-lea. se creează conceptul general de spațiu în spațiu (metric ≈ M. Fréchet, topologic ≈ F. Hausdorff), apar ideile inițiale ale teoriei dimensiunii și se demonstrează cele mai simple teoreme privind mapările continue (A. Lebesgue, L. Brouwer) , se introduc poliedre (H. Poincaré) și se determină așa-numitele numere Betti ale acestora. Primul sfert al secolului XX. se încheie cu înflorirea topologiei generale și crearea școlii topologice de la Moscova; se pun bazele teoriei generale a dimensiunii (P. S. Uryson); axiomaticii spaţiilor topologice i se dă forma sa modernă (P. S. Aleksandrov); se construiește teoria spațiilor compacte (Alexandrov, Uryson) și se demonstrează teorema asupra produsului lor (A. N. Tikhonov); pentru prima dată sunt date condiții necesare și suficiente pentru metrizabilitatea spațiului (Alexandrov, Uryson); este introdus conceptul de acoperire local finită (Alexandrov) [pe baza căreia în 1944 J. Dieudonné (Franţa) a definit spaţiile paracompacte]; sunt introduse spații complet regulate (Tikhonov); se definește conceptul de nerv și astfel se întemeiază teoria generală a omologiei (Alexandrov). Sub influența lui E. Noether, numerele Betti sunt recunoscute ca rânduri ale grupurilor de omologie, care sunt, prin urmare, numite și grupuri Betti. L. S. Pontryagin, pe baza teoriei sale a caracterelor, demonstrează legile dualității pentru mulțimi închise.

În al 2-lea sfert al secolului al XX-lea. Dezvoltarea teoriei generale și a teoriei omologiei continuă: în dezvoltarea ideilor lui Tihonov, A. Stone (SUA) și E. Cech introduc așa-numita piatră ≈ Cehov, sau extinderea maximă, (bi)compactă a unui spațiu complet regulat; Sunt definite grupuri de omologie ale spațiilor arbitrare (Cech), se introduce multiplicarea în grupuri de coomologie (J. Alexander, A. N. Kolmogorov) și se construiește un inel de coomologie. În acest moment, în teoria algebrică domneau metode combinatorii bazate pe luarea în considerare a schemelor simple; Prin urmare, teoria algebrică se mai numește uneori teorie combinatorie.Se introduc spațiile de proximitate și spațiile uniforme. Teoria homotopilor începe să se dezvolte intens (H. Hopf, Pontryagin); sunt definite grupuri de homotopie (V. Gurevich, SUA) și se aplică considerații de teorie netedă la calculul lor (Pontriagin). Sunt formulate axiomele grupărilor de omologie și coomologie (N. Steenrod și S. Eilenberg, SUA). Apare teoria fasciculelor (H. Whitney, SUA; Pontryagin); sunt introduse spații celulare (J. Whitehead, Marea Britanie).

În a doua jumătate a secolului al XX-lea. În URSS se formează școala sovietică de teorie generală și teoria omologiei: se lucrează la teoria dimensiunii, problema metrizării, teoria extensiilor (bi)compacte, teoria generală a mapărilor continue (factoriale, etc.). deschis, închis), în special teoria absolutelor; teorii ale așa-numitelor invarianți cu valori cardinale (A.V. Arkhangelsky, B.A. Pasynkov, V.I. Ponomarev, E.G. Sklyarenko, Yu.M. Smirnov etc.).

Prin eforturile unui număr de oameni de știință (J. P. Serres și A. Cartan în Franța, M. M. Postnikov în URSS, Whitehead etc.), s-a format în sfârșit teoria homotopilor. În acest moment, au fost create centre mari de teorie algebrică în SUA, Marea Britanie și alte țări; interesul pentru teoria geometrică este reînnoit.Se creează teoria fasciculelor vectoriale și a functorului K (M. Atiyah, Marea Britanie; F. Hirzebruch, Germania), teoria algebrică este utilizată pe scară largă în teoria smooth (R. Thom, Franța) și geometrie algebrică (Hirzebruch); Se dezvoltă teoria (co)bordismelor (V.A. Rokhlin, URSS; Tom, S.P. Novikov) și teoria netezirii și triangulabilității (J. Milnor, SUA).

Dezvoltarea tehnologiei continuă în toate direcțiile, iar domeniul de aplicare al aplicațiilor sale este în continuă extindere.

A. A. Maltsev.

═Ref.: Aleksandrov P.S., Introducere în teoria generală a mulțimilor și funcțiilor, M.≈L., 1948; Parkhomenko A. S., Ce este o linie, M., 1954; Pontryagin L.S., Fundamentele topologiei combinatorii, M.≈L., 1947; de el, Grupuri continue, ed. a III-a, M., 1973; Milnor J., Wallace A, Topologie diferențială. Curs de început, trad. din engleză, M., 1972; Steenrod N., Chinn W., Primele concepte de topologie, trad. din engleză, M., 1967; Aleksandrov P. S., Topologie combinatorie, M.≈L., 1947; Aleksandrov P. S., Pasynkov B. A., Introducere în teoria dimensiunilor. Introducere în teoria spațiilor topologice și teoria generală a dimensiunii, M., 1973; Aleksandrov P.S., Introducere în teoria omologică a dimensiunii și topologia combinatorie generală, M., 1975; Arkhangelsky A.V., Ponomarev V.I., Fundamentele topologiei generale în probleme și exerciții, M., 1974; Postnikov M. M., Introducere în teoria Morse, M., 1971; Bourbaki N., Topologie generală. Structuri de bază, trad. din franceză, M., 1968; lui, Topologie generală. Grupuri topologice. Numere și grupuri și spații aferente, trad. din franceză, M., 1969; lui, Topologie generală. Utilizarea numerelor reale în topologia generală. Spații funcționale. Rezumatul rezultatelor. Dicţionar, trans. din franceză, M., 1975; Kuratovsky K., Topologie, trad. din engleză, vol. 1≈2, M., 1966≈69; Lang S., Introducere în teoria varietăților diferențiabile, trad. din engleză, M., 1967; Spenier E., Topologie algebrică, trad. din engleză, M., 1971.

Topologie (dezambiguizare)

Topologie:

• Topologia este o ramură a matematicii care studiază fenomenul continuității în forma sa cea mai generală.
• Topologia este un sistem de mulțimi utilizat în definirea unui spațiu topologic.
• Topologia rețelei este o diagramă a locației și conexiunii dispozitivelor de rețea.

Exemple de utilizare a cuvântului topologie în literatură.

Pontryagin, prin ale cărui eforturi a fost creată o nouă ramură a matematicii - algebra topologică - studiind diferite structuri algebrice înzestrate cu topologie.

Și nu se poate înțelege histologia fără hidrologie, hidrologie fără geologie, geologie fără geografie, geografie fără topografie, topografie fără topologieși toate împreună fără omneologie, și omneologie - fără tabele.

Nu am înțeles histologia, nu am înțeles hidrologia, hidrografia, geografia, topografia, topologie.

În general, această abordare presupune documentarea rețelei topologie, programe de aplicație și protocoale utilizate.

Așa că a continuat, folosind termeni din ce în ce mai complicati, referindu-se la topologie spiritul și geometria conștientizării și a perspicacității, expunând elementele ontografiei endoscopice, climatizarea vieții emoționale, nivelurile sale, extremele, suișurile, coborâșurile, precum și scăderile spiritului și a vorbit atât de mult încât a devenit răgușit, iar regele avea dureri de cap.

Carduri topologie Rutarea e-mailului este utilă pentru rezolvarea problemelor legate de transferul de e-mail între servere.

De asemenea, sperăm să vedem o bibliotecă de rezoluție de nivel superior care sortează răspunsurile pe baza informațiilor despre topologie, existent doar pe gazda client.

Aceasta înseamnă că rețeaua topologie iar segmentarea devine un important factor protector.

La urma urmei, în esență, orice teorie se rezumă la topologie imagini, iar orice ontologie nu este altceva decât un complex deductiv de imagini universale, legate inductiv de realitatea empirică.

A crea topologie servere la distanță, mai întâi determinați bazele de date pe care stațiile de lucru și serverele le vor accesa cel mai frecvent.

Și anume - în lumea continuumului topologie conexiunile sale interne ne permit să constituim un mediu în care intersubiectivitatea devine o funcție a distribuției raționalităților în cadrul acesteia.

Adică, potrivit obiectivistului topologieÎn lumea corpusculară, problema intersubiectivității este rezolvată în ea cu ajutorul unui mediator intersubstanțial.

Vorbim despre unele topologii spații care se încadrează unul în celălalt, se transformă unul în celălalt, așa cum literele apar sub diferite aspecte sau se alternează în monograma unei ferestre.

Cu toate acestea, în organizațiile mici, acest lucru topologie garantează actualizarea rapidă a datelor.

Pentru că plănuiești topologie, Ar trebui să luați în considerare și topologie traficul de corespondență și replicare.