Todo comenzó con el hecho de que un amigo de un amigo de mi amigo necesitaba ayuda con estos mismos filtros. A través de los caminos Jedi, me llegaron rumores sobre esto, me di de baja en los comentarios a la publicación en el enlace. Parece haber ayudado. Bueno, espero.
Esta historia despertó en mí los recuerdos de mi tercer año, o algo así, cuando pasé el DSP yo mismo, y me inspiró a escribir un artículo para todos aquellos que están interesados \u200b\u200ben cómo funcionan los filtros digitales, pero que están naturalmente asustados por fórmulas de alta seguridad y dibujos psicodélicos en (ya No estoy hablando de libros de texto).
En general, en mi experiencia, la situación con los libros de texto se describe con la famosa frase sobre el hecho de que el bosque no es visible detrás de los árboles. Y es decir, cuando empiezan a asustarle directamente con las fórmulas de transformación Z y división polinomial, que a menudo son más largas que dos tableros, el interés en el tema se agota muy rápido. Empezaremos por uno sencillo, ya que no es necesario pintar expresiones largas y complejas para entender lo que está pasando.
Primero, algunos conceptos básicos simples.
1. Respuesta de impulso.
Digamos que tenemos una caja con cuatro pines. No tenemos idea de lo que hay dentro, pero sabemos con certeza que los dos pines de la izquierda son la entrada y los dos pines de la derecha son la salida. Intentemos aplicarle un pulso muy corto de amplitud muy grande y veamos qué sucede en la salida. Bueno, pues, da lo mismo que dentro de este cuatripolar no está claro, porque cómo describirlo no está claro, pero al menos veremos algo.
Aquí debe decirse que un pulso corto (en general, infinitamente corto) de gran amplitud (en general, infinita) se llama función delta en teoría. Por cierto, lo curioso es que la integral de este sin fin la función es igual a uno. Esa es la normalización.
Entonces, lo que vimos en la salida de una red de cuatro puertos al aplicar una función delta a la entrada se llama respuesta impulsiva este de cuatro polos. Sin embargo, hasta ahora no está claro cómo nos ayudará, pero ahora recordemos el resultado y pasemos al siguiente concepto interesante.
2. Convolución.
En resumen, la convolución es una operación matemática que se reduce a integrar el producto de funciones:
![]()
Se indica, como puede ver, con un asterisco. También puede ver que durante la convolución, una función se toma en su orden "directo" y pasamos la segunda "al revés". Por supuesto, en un caso discreto, que es más valioso para la humanidad, la convolución, como cualquier integral, pasa a sumar:

Parecería una especie de aburrida abstracción matemática. Sin embargo, de hecho, el paquete es quizás el fenómeno más mágico de este mundo, sorprendentemente solo superado por el nacimiento de una persona en el mundo, con la única diferencia de que de donde vienen los niños, la mayoría de las personas aprenden al menos a la edad de dieciocho años, mientras que sobre eso, lo que es una convolución y lo útil y sorprendente que es, una gran parte de la población mundial no tiene ni idea durante toda su vida.
Entonces, el poder de esta operación radica en el hecho de que si f es cualquier señal de entrada arbitraria yg es la respuesta al impulso de una red de cuatro puertos, entonces el resultado de la convolución de estas dos funciones será similar al que obtendríamos si pasamos la señal f a través de esta red de cuatro puertos.
Es decir, la respuesta al impulso es un elenco completo de todas las propiedades del cuadrupolo en relación con la acción de entrada, y la convolución de la señal de entrada con él le permite restaurar la señal de salida correspondiente. En cuanto a mí, ¡esto es simplemente increíble!
3. Filtros.
Puede hacer mucho con la respuesta al impulso y la convolución. Por ejemplo, si la señal es sonora, puede organizar reverberación, eco, coro, flanger y mucho, mucho más; se pueden diferenciar e integrar ... En general, crear cualquier cosa. Lo más importante para nosotros ahora es que, por supuesto, utilizando la convolución, los filtros se obtienen con la misma facilidad.
El filtro digital en sí es la convolución de la señal de entrada con una respuesta de impulso correspondiente al filtro deseado.
Pero, por supuesto, la respuesta al impulso debe obtenerse de alguna manera. Por supuesto, ya hemos descubierto cómo medirlo anteriormente, pero esta tarea tiene poco sentido: si ya hemos ensamblado un filtro, ¿por qué más deberíamos medir algo? Puede usarlo tal como está. Y además, el valor más importante de los filtros digitales es que pueden tener características inalcanzables (o muy difíciles de lograr) en la realidad, por ejemplo, una fase lineal. Así que no hay forma de medir en absoluto, solo necesitas contar.
4. Obtener una respuesta impulsiva.
En este punto, en la mayoría de las publicaciones sobre el tema, los autores comienzan a descargar montañas de transformaciones Z y fracciones de polinomios en el lector, confundiéndolo por completo. No haré esto, solo explicaré brevemente para qué sirve todo esto y por qué en la práctica no es muy necesario para el público progresista.
Supongamos que averiguamos lo que queremos del filtro e hicimos una ecuación que lo describe. Además, para encontrar la respuesta al impulso, puede sustituir la función delta en la ecuación derivada y obtener la deseada. El único problema es cómo hacerlo, porque el delta funciona en el tiempo acerca dela zona está determinada por un sistema astuto y, en general, hay todo tipo de infinitos. Entonces, en esta etapa, todo resulta terriblemente difícil.
Aquí sucede, y recuerdan que existe la transformada de Laplace. Por sí solo, no es una libra de pasas. La única razón por la que se tolera en la ingeniería de radio es precisamente el hecho de que en el espacio del argumento, la transición a la que es esta transformación, algunas cosas realmente se vuelven más simples. En particular, la función delta que nos dio tantos problemas en el dominio del tiempo se expresa muy fácilmente: ¡allí es solo una unidad!
La transformación Z (también conocida como transformación Laurent) es una versión discreta de la transformación de Laplace.
Es decir, aplicando la transformada de Laplace (o transformada Z, si es necesario) a la función que describe el filtro deseado, sustituyendo uno en el resultante y transformándolo de nuevo, obtenemos la respuesta al impulso. Suena fácil, cualquiera puede probarlo. No me arriesgaré, porque, como ya se mencionó, la transformada de Laplace es algo duro, sobre todo lo contrario. Dejémoslo como último recurso, y nosotros mismos buscaremos formas más sencillas de conseguir lo que buscamos. Hay muchos de ellos.
En primer lugar, podemos recordar otro hecho sorprendente de la naturaleza: las características de amplitud-frecuencia e impulso están conectadas entre sí por la amable y familiar transformada de Fourier. Esto significa que podemos dibujar cualquier respuesta de frecuencia a nuestro gusto, tomar de ella la transformada de Fourier inversa (aunque continua, incluso discreta) y obtener la respuesta de impulso del sistema que la implementa. ¡Es simplemente asombroso!
Aquí, sin embargo, no funcionará sin problemas. En primer lugar, es probable que la respuesta de impulso que obtengamos sea infinita (no explicaré por qué; así es como funciona el mundo), por lo que tendremos que cortarla en algún momento (poniéndola igual a cero más allá de este punto) mediante una decisión deliberada. Pero no funcionará así; como resultado de esto, como era de esperar, habrá distorsiones de la respuesta de frecuencia del filtro calculado, se volverá ondulado y el corte de frecuencia se difuminará.
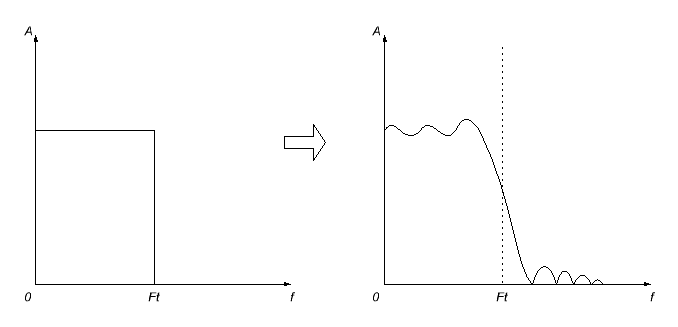
Para minimizar estos efectos, se aplican varias funciones de ventana de suavizado a la respuesta de impulso acortada. Como resultado, la respuesta de frecuencia suele ser aún más borrosa, pero las oscilaciones desagradables (especialmente en la banda de paso) desaparecen. 
En realidad, después de dicho procesamiento, obtenemos una respuesta de impulso operativo y podemos construir un filtro digital.
El segundo método de cálculo es aún más simple: las respuestas de impulso de los filtros más populares se han expresado durante mucho tiempo en forma analítica para nosotros. Solo queda sustituir sus valores y aplicar una función de ventana al resultado a su gusto. Así que ni siquiera necesitas contar las transformaciones.
Y, por supuesto, si el objetivo es emular el comportamiento de un circuito en particular, puede obtener su respuesta de impulso en el simulador:

Aquí apliqué un pulso de 100500 voltios (sí, 100,5 kV) con una duración de 1 μs a la entrada del circuito RC y obtuve su respuesta de impulso. Está claro que en realidad esto no se puede hacer, pero en el simulador, este método, como puede ver, funciona muy bien.
5. Notas.
Lo anterior sobre el acortamiento de la respuesta al impulso, por supuesto, se refería a los llamados. Filtros de respuesta de impulso finito (FIR / FIR). Tienen muchas propiedades valiosas, incluida la fase lineal (bajo ciertas condiciones de respuesta de impulso), que no produce distorsión de la señal durante el filtrado, así como una estabilidad absoluta. También hay filtros con respuesta de impulso infinita (filtros IIR / IIR). Consumen menos recursos en términos de cálculos, pero ya no tienen las ventajas enumeradas.
En el próximo artículo, espero mostrarles un ejemplo sencillo de una implementación práctica de un filtro digital.
Conferencia número 10
Filtros digitales de respuesta de impulso finito
La función de transferencia de un filtro de respuesta de impulso finito digital físicamente realizable (filtro FIR) se puede representar como
(10.1).
Al reemplazar en la expresión (10.1), obtenemos la respuesta de frecuencia del filtro FIR en la forma
![]() (10.2),
(10.2),
dónde ![]() - característica de amplitud-frecuencia (AFC) filtrar,
- característica de amplitud-frecuencia (AFC) filtrar,
![]() - característica de frecuencia de fase (PFC) filtrar.
- característica de frecuencia de fase (PFC) filtrar.
Retardo de fase el filtro se define como
![]() (10.3).
(10.3).
Retraso de grupo el filtro se define como
![]() (10.4).
(10.4).
Una característica distintiva de los filtros FIR es la capacidad de implementar retardos constantes de fase y grupo en ellos, es decir, respuesta de fase lineal
(10.5),
donde un es una constante. Si se cumple esta condición, la señal que pasa a través del filtro no distorsiona su forma.
Para derivar las condiciones que proporcionan una respuesta de fase lineal, escribimos la respuesta de frecuencia del filtro FIR teniendo en cuenta (10.5)
![]() (10.6).
(10.6).
Al equiparar las partes real e imaginaria de esta igualdad, obtenemos
 (10.7).
(10.7).
Dividiendo la segunda ecuación por la primera, obtenemos
 (10.8).
(10.8).
Finalmente, puedes escribir
 (10.9).
(10.9).
Esta ecuación tiene dos soluciones. El primero enun \u003d 0 corresponde a la ecuación
 (10.10).
(10.10).
Esta ecuación tiene una solución única correspondiente a un arbitrarioh (0) (sin (0) \u003d 0) y h (n) \u003d 0 para n \u003e 0. Esta solución corresponde a un filtro cuya respuesta de impulso tiene un único recuento distinto de cero en el momento inicial. Dicho filtro no tiene ningún interés práctico.
Busquemos otra solución para. En este caso, multiplicando de forma cruzada los numeradores y denominadores en (10.8), obtenemos
(10.11).
Por lo tanto tenemos
![]() (10.12).
(10.12).
Dado que esta ecuación tiene la forma de una serie de Fourier, su solución, si existe, es única.
Es fácil ver que la solución de esta ecuación debe satisfacer las condiciones
(10.13),
(10.14).
De la condición (10.13) se deduce que para cada orden de filtronorte solo hay un retardo de faseun , en el que se puede lograr una estricta linealidad de la respuesta de fase. De la condición (10.14) se deduce que la respuesta al impulso del filtro debe ser simétrica con respecto al punto para unnorte y relativo al punto medio del intervalo (Figura 10.1).
 |
La respuesta de frecuencia de dicho filtro (por un extrañonorte ) Se puede escribir como
(10.15).
Haciendo una sustitución en la segunda cantidadm \u003d N -1- n, obtenemos
(10.16).
Dado que h (n) \u003d h (N -1- n ), entonces las dos sumas se pueden combinar
 (10.17).
(10.17).
Sustituyendo, obtenemos
(10.18).
Si denotamos
 (10.19),
(10.19),
entonces finalmente podemos escribir
 (10.20).
(10.20).
Por lo tanto, para un filtro con una respuesta de fase lineal, tenemos
 (10.21).
(10.21).
Para el caso de inclusonorte de manera similar tendremos
 (10.22).
(10.22).
Haciendo una sustitución en la segunda suma, obtenemos
 (10.23).
(10.23).
Haciendo un reemplazo, obtenemos
(10.24).
Designando
![]() (10.25),
(10.25),
finalmente tendrá
 (10.26).
(10.26).
Por lo tanto, para un filtro FIR con una respuesta de fase lineal y un orden parN se puede escribir
 (10.27).
(10.27).
En lo que sigue, por simplicidad, consideraremos solo filtros con un orden impar.
Al sintetizar la función de transferencia del filtro, los parámetros iniciales son, por regla general, los requisitos para la respuesta de frecuencia. Existen muchas técnicas para sintetizar filtros FIR. Consideremos algunos de ellos.
Dado que la respuesta de frecuencia de cualquier filtro digital es una función periódica de la frecuencia, se puede representar como una serie de Fourier
![]() (10.28),
(10.28),
donde los coeficientes de la serie de Fourier son
 (10.29).
(10.29).
Se ve que los coeficientes de la serie de Fourierh (n ) coinciden con los coeficientes de la respuesta al impulso del filtro. Por lo tanto, si se conoce la descripción analítica de la respuesta de frecuencia requerida del filtro, entonces es fácil determinar los coeficientes de la respuesta al impulso a partir de ella y, a partir de ellos, la función de transferencia del filtro. Sin embargo, en la práctica esto no es factible, ya que la respuesta al impulso de dicho filtro tiene una longitud infinita. Además, dicho filtro no se puede realizar físicamente ya que la respuesta al impulso comienza en -¥ , y ningún retraso finito hará que este filtro sea físicamente realizable.
Uno de los posibles métodos para obtener un filtro FIR que se aproxime a una respuesta de frecuencia dada es truncar la serie infinita de Fourier y la respuesta al impulso del filtro, asumiendo queh (n) \u003d 0 para. Luego
 (10.30).
(10.30).
Viabilidad física de la función de transferenciaH (z ) se puede lograr multiplicandoH (z) encendido.
 (10.31),
(10.31),
dónde
(10.32).
Con esta modificación de la función de transferencia, la característica de amplitud del filtro no cambia y el retardo de grupo aumenta en un valor constante.
Como ejemplo, calculemos un filtro FIR de paso bajo con una respuesta de frecuencia de la forma
 (10.33).
(10.33).
De acuerdo con (10.29), los coeficientes de respuesta al impulso del filtro se describen mediante la expresión
 (10.34).
(10.34).
Ahora de (10.31) se puede obtener una expresión para la función de transferencia
 (10.35),
(10.35),
dónde
(10.36).
Características de amplitud del filtro calculado para variosnorte se presentan en la Figura 10.2.

Figura 10.2
La ondulación en la banda de paso y la banda de parada se produce debido a la lenta convergencia de la serie de Fourier, que, a su vez, se debe a la presencia de una discontinuidad en la función en la frecuencia de corte de la banda de paso. Estas ondas se conocen como ondulación de Gibbs.
La figura 10.2 muestra que al aumentarnorte la frecuencia de ondulación aumenta, mientras que la amplitud disminuye tanto en las frecuencias más bajas como en las más altas. Sin embargo, la amplitud de la última ondulación en la banda de paso y la primera ondulación en la banda de supresión permanecen prácticamente sin cambios. En la práctica, tales efectos a menudo son indeseables, lo que requiere encontrar formas de reducir las pulsaciones de Gibbs.
Respuesta de impulso truncadah (n ) se puede representar como el producto de la respuesta de impulso infinita requerida y algunos funciones de ventana w (n) de longitud n (Figura 10.3).
![]() (10.37).
(10.37).
 |
En el caso considerado de un truncamiento simple de la serie de Fourier, usamos ventana rectangular
 (10.38).
(10.38).
En este caso, la respuesta de frecuencia del filtro se puede representar como una convolución compleja
 (10.39).
(10.39).
Esto significa que será una versión "borrosa" de la característica requerida.
El problema se reduce a encontrar las funciones de ventana que permitan reducir las pulsaciones de Gibbs con la misma selectividad de filtro. Para hacer esto, primero debe estudiar las propiedades de la función de ventana usando el ejemplo de una ventana rectangular.
El espectro de la función de ventana rectangular se puede escribir como
 (10.40).
(10.40).
El espectro de la función de ventana rectangular se muestra en la Figura 10.4.

Figura 10.4
Dado que en, el ancho del lóbulo principal del espectro resulta ser.
La presencia de lóbulos laterales en el espectro de la función de ventana conduce a un aumento de la ondulación de Gibbs en la respuesta de frecuencia del filtro. Para obtener una pequeña ondulación en la banda de paso y una gran atenuación en la banda de supresión, es necesario que el área delimitada por los lóbulos laterales sea una pequeña fracción del área delimitada por el lóbulo principal.
A su vez, el ancho del lóbulo principal determina el ancho de la zona de transición del filtro resultante. Para una alta selectividad de filtro, el ancho del lóbulo principal debe ser lo más pequeño posible. Como se ve en lo anterior, el ancho del lóbulo principal disminuye al aumentar el orden del filtro.
Por tanto, las propiedades de las funciones de ventana adecuadas se pueden formular de la siguiente manera:
- la función de ventana debe estar limitada en el tiempo;
- el espectro de la función de ventana debe aproximarse mejor a la función de frecuencia limitada, es decir tener un mínimo de energía fuera del lóbulo principal;
- el ancho del lóbulo principal del espectro de la función de ventana debe ser lo más pequeño posible.
Las funciones de ventana más utilizadas son:
1. Ventana rectangular. Considerado arriba.
2. Ventana de Hamming.
 (10.41),
(10.41),
dónde.
Cuando esta ventana se llama ventana de Henn (hanning).
3. Ventana de Blackman.
 (10.42).
(10.42).
4. Ventana de Bartlett.
 (10.43).
(10.43).
Los indicadores de los filtros construidos utilizando las funciones de ventana especificadas se resumen en la Tabla 10.1.
|
Ventana |
Ancho del lóbulo principal |
Factor de ondulación,% |
||
N \u003d 11 |
N \u003d 21 |
N \u003d 31 |
||
|
Rectangular |
22.34 |
21.89 |
21.80 |
|
|
Hanning |
2.62 |
2.67 |
2.67 |
|
|
Hamming |
1.47 |
0.93 |
0.82 |
|
|
Hombre negro |
0.08 |
0.12 |
0.12 |
|
El factor de ondulación se define como la relación entre la amplitud máxima del lóbulo lateral y la amplitud del lóbulo principal en el espectro de la función de ventana.
Para seleccionar el orden de filtro requerido y la función de ventana más apropiada al calcular filtros reales, puede usar los datos de la Tabla 10.2.
|
transicional |
Desigualdad transmisión (dB) |
Atenuación en barreras (dB) |
|
|
Rectangular |
|||
|
Hanning |
|||
|
Hamming |
|||
|
Hombre negro |
Como puede verse en la tabla 10.1, existe una relación definida entre el factor de ondulación y el ancho del lóbulo principal en el espectro de la función de ventana. Cuanto menor sea el coeficiente de ondulación, mayor será la anchura del lóbulo principal y, por tanto, la zona de transición en la respuesta de frecuencia del filtro. Para garantizar una baja ondulación en la banda de paso, es necesario elegir una ventana con un coeficiente de ondulación adecuado y proporcionar el ancho requerido de la zona de transición con un orden de filtro mayor N.
Este problema se puede resolver con la ayuda de la ventana sugerida por Kaiser. La función de la ventana de Kaiser tiene la forma
 (10.44),
(10.44),
donde a es un parámetro independiente, ![]() , I 0 es la función de Bessel de orden cero del primer tipo, definida por la expresión
, I 0 es la función de Bessel de orden cero del primer tipo, definida por la expresión
 (10.45).
(10.45).
Una propiedad atractiva de la ventana de Kaiser es la capacidad de cambiar suavemente el coeficiente de ondulación de valores pequeños a valores grandes cuando solo se cambia un parámetro a. En este caso, como para otras funciones de ventana, el ancho del lóbulo principal se puede ajustar por el orden de filtro N.
Los principales parámetros que se establecen al desarrollar un filtro real son:
Ancho de banda - w p;
Franja de obstáculos - w a;
La ondulación máxima permitida en la banda de paso - A p;
Atenuación mínima en la banda de supresión - A a;
-frecuencia de muestreo -w s.
Estos parámetros se ilustran en la Figura 10.5. En este caso, la ondulación máxima en la banda de paso se define como
![]() (10.46),
(10.46),
y la atenuación mínima en la banda de supresión como
Un procedimiento relativamente simple para calcular un filtro con una ventana de Kaiser incluye los siguientes pasos:
1.Se determina la respuesta al impulso del filtro h (n), siempre que la respuesta de frecuencia sea ideal
 (10.48),
(10.48),
donde (10,49).
2. El parámetro d se selecciona como
![]() (10.50),
(10.50),
dónde  (10.51).
(10.51).
3. El verdadero valor de A a y A p se calcula mediante las fórmulas (10.46), (10.47).
4.Elija el parámetro a como
 (10.52).
(10.52).
5. Seleccione el parámetro D como
 (10.53).
(10.53).
6. El valor impar más pequeño del orden de filtrado se selecciona de la condición
![]() (10.54),
(10.54),
 (10.57)
(10.57)
sigue que
Dado que las muestras de la respuesta al impulso del filtro son los coeficientes de su función de transferencia, la condición (10.59) significa que los códigos de todos los coeficientes del filtro contienen solo una parte fraccionaria y un bit de signo y no contienen una parte entera.
El número de bits de la parte fraccionaria de los coeficientes del filtro se determina a partir de la condición de satisfacer la función de transferencia del filtro con coeficientes cuantificados, los requisitos especificados para la aproximación a la función de transferencia de referencia con valores exactos de los coeficientes.
Los valores absolutos de las muestras de las señales de entrada del filtro suelen normalizarse de modo que
Si el análisis se realiza para un filtro FIR con una respuesta de fase lineal, entonces el algoritmo para calcular su señal de salida puede ser el siguiente
donde se redondean los coeficientes del filtro a s k.
Este algoritmo corresponde al diagrama de bloques del filtro que se muestra en la figura 10.5.
 |
Hay dos formas de implementar este algoritmo. En el primer caso, todas las operaciones de multiplicación se realizan exactamente y no hay redondeo de productos. En este caso, la longitud de palabra de los productos es igual as en + s k, donde s en es el ancho de la señal de entrada y s k es el ancho de los coeficientes del filtro. En este caso, el diagrama de bloques del filtro que se muestra en la figura 10.5 corresponde exactamente al filtro real.
En la segunda forma de implementar el algoritmo (10.61), cada resultado de la operación de multiplicación se redondea, es decir los productos se calculan con algún error. En este caso, es necesario cambiar el algoritmo (10.61) para tener en cuenta el error introducido al redondear los productos.
Si los valores de muestra de la señal de salida del filtro se calculan de acuerdo con el primer método (con valores exactos de los productos), entonces la varianza del ruido de salida se determina como
![]() (10.66),
(10.66),
aquellos. depende de la varianza del ruido de redondeo de la señal de entrada y de los valores de los coeficientes del filtro. Desde aquí puede encontrar el número requerido de bits de la señal de entrada como
 (10.67).
(10.67).
A partir de los valores conocidos de s en y s k, se puede determinar el número de bits necesarios para la parte fraccionaria del código de la señal de salida como
Si los valores de muestra de la señal de salida se calculan de acuerdo con el segundo método, cuando cada producto se redondea a s d bits, entonces la varianza del ruido de redondeo generado por cada uno de los multiplicadores se puede expresar en términos del ancho del producto como
DR in y relación señal / ruido en la salida del filtro SNR out. El valor del rango dinámico de la señal de entrada en decibelios se define como
![]() (10.74),
(10.74),
donde A max y A min son las amplitudes máxima y mínima de la señal de entrada del filtro.
La relación señal-ruido en la salida del filtro, expresada en decibelios, se define como
![]() (10.75),
(10.75),
determina el valor cuadrático medio de la potencia de la señal sinusoidal de salida del filtro con amplitud A min, y
(10.77)
determina la potencia de ruido a la salida del filtro. De (10.75) y (10.76) con A max \u003d 1 obtenemos una expresión para la varianza del ruido de salida del filtro
![]() (10.78).
(10.78).
Este valor de la varianza del ruido de salida del filtro se puede utilizar para calcular los anchos de las señales de entrada y salida del filtro.
Consideremos el más simple de los filtros digitales: filtros con parámetros constantes.
La señal de entrada se envía a la entrada del filtro digital en forma de una secuencia de valores numéricos que siguen con un intervalo (Fig. 4.1, a). Cuando se recibe cada valor de la siguiente señal en el filtro digital, se calcula el siguiente valor de la señal de salida Los algoritmos de cálculo pueden ser muy diversos; durante el cálculo, además del último valor de la señal de entrada,
valores previos de las señales de entrada y salida: La señal a la salida del filtro digital es también una secuencia de valores numéricos, seguida de un intervalo. Este intervalo es el mismo para todo el dispositivo de procesamiento de señales digitales.

Figura: 4.1. Señal en la entrada y salida del filtro digital
Por lo tanto, si la señal más simple en forma de un solo impulso se aplica a la entrada del filtro digital (figura 4.2, a)
![]()
luego en la salida recibiremos una señal en forma de una secuencia discreta de valores numéricos, seguida de un intervalo
Por analogía con los circuitos analógicos convencionales, llamemos a esta señal de respuesta la respuesta de impulso del filtro (figura 4.2, b). A diferencia de la respuesta al impulso de un circuito analógico, la función es adimensional.

Figura: 4.2. Respuesta de impulso de un solo impulso y filtro digital
Apliquemos una señal discreta arbitraria a la entrada del filtro Fig. 4.1, a), que es un conjunto de valores discretos
Bajo la acción del primer elemento a la salida del filtro, se forma una secuencia multiplicada por la secuencia multiplicada por y desplazada a la derecha por una cantidad, etc. Como resultado, en la salida, obtenemos una secuencia con

Por tanto, la señal de salida se define como una convolución discreta de la señal de entrada y la respuesta al impulso. En este sentido, los filtros digitales son similares a los circuitos convencionales, donde la salida es igual a la convolución de la entrada y la respuesta al impulso.
La fórmula (4.1) es un algoritmo de filtrado digital. Si la respuesta al impulso del filtro se describe mediante una secuencia con un número finito de miembros, entonces el filtro se puede implementar como un circuito que se muestra en la Fig. 4.3. Aquí la letra denota los elementos del retardo de la señal por un tiempo (para una celda); -Elementos que multiplican la señal por el factor adecuado.
El circuito que se muestra en la Fig. 4.3 no es un circuito de filtro digital; este diagrama es una representación gráfica del algoritmo de filtrado digital y muestra la secuencia de operaciones aritméticas realizadas durante el procesamiento de la señal.

Figura: 4.3. Circuito de filtro digital no recursivo
Para los filtros digitales que procesan señales en forma de secuencias numéricas abstractas, el concepto de "retardo de tiempo" no es del todo correcto. Por lo tanto, los elementos que retrasan la señal por celda suelen estar marcados en los circuitos de filtro digital con un símbolo que indica el retraso de la señal en el lenguaje de las transformaciones. En lo que sigue, nos adheriremos a esta designación.
Volvamos al circuito de filtro digital que se muestra en la Fig. 4.3 Los filtros que utilizan solo valores de señal de entrada para el cálculo se denominan simples o no recursivos.
Un algoritmo de filtro no recursivo es fácil de escribir si se conoce la respuesta al impulso del filtro. Para la implementación práctica del algoritmo, es necesario que la respuesta al impulso contenga un número finito de términos. Si la respuesta al impulso contiene un número infinito de términos, pero su magnitud disminuye rápidamente, entonces podemos restringirnos a un número finito de términos, descartando aquellos cuyos valores son pequeños. Si los elementos de la respuesta al impulso no disminuyen en magnitud, el algoritmo de filtro no recursivo resulta irrealizable.

Figura: 4.4. -cadena
Como ejemplo, considere el filtro digital más simple similar a la cadena (Fig. 4.4). La respuesta al impulso de la cadena tiene la forma
![]()
Para escribir la respuesta al impulso del filtro digital correspondiente, la expresión debe reemplazarse por Sin embargo, la respuesta al impulso de la cadena -es adimensional y la respuesta al impulso del filtro digital debe ser adimensional. Por lo tanto, omitimos el factor en la expresión (4.2) y escribimos la respuesta al impulso del filtro digital en la forma
![]()
Tal respuesta de impulso contiene infinitos términos, pero su valor disminuye exponencialmente, y puede limitarse a términos, eligiendo tales que
Ahora puede escribir una expresión para la señal en la salida del filtro.
Esta expresión también es un algoritmo de filtro digital. El diagrama de este filtro se muestra en la Fig. 4.5.
El segundo enfoque para el análisis de procesos en filtros digitales es similar al método del operador para analizar circuitos analógicos convencionales, solo que en lugar de la transformada de Laplace, se utiliza la transformación-.

Figura: 4.5. Diagrama de un filtro digital no recursivo similar a la cadena
Definamos el parámetro del filtro digital, similar a la función de transferencia del circuito eléctrico. Para hacer esto, aplique la conversión -a la respuesta de impulso del filtro digital:

La función se denomina función de filtro del sistema.
De acuerdo con la expresión (4.1), la señal en la salida del filtro digital es igual a la convolución discreta de la señal de entrada y la respuesta al impulso del filtro. Aplicando el teorema de la transformada de convolución a esta expresión, obtenemos que la -transformación de la señal de salida es igual a la -transformación de la señal de entrada multiplicada por la función de filtro del sistema:
![]()
Por lo tanto, la función del sistema juega el papel de la función de transferencia de filtro digital.
Como ejemplo, busquemos la función del sistema de un filtro digital de primer orden similar a la cadena:

El tercer método para analizar el paso de señales a través de filtros digitales es similar al método clásico de ecuaciones diferenciales. Consideremos este método usando el ejemplo de cadenas de pedidos.
El circuito analógico más simple de primer orden es una cadena (véase la figura 4.4), cuyo paso de señales se describe mediante la ecuación diferencial
![]()
Para un circuito discreto, en lugar de la ecuación diferencial (4.8), se debe escribir una ecuación en diferencia, donde las señales de entrada y salida se especifican para momentos discretos de tiempo y la diferencia de los valores de la señal adyacente debe aparecer en lugar de la derivada. Para una cadena discreta de primer orden, la ecuación en diferencias se puede escribir en una forma bastante general
Aplicamos a la ecuación -transformación
de donde encontramos la función de filtro del sistema
![]()
La fórmula (4.10) es una expresión bastante general para la función del sistema del filtro digital de primer orden. Cuando, coincide con la expresión (4.7) obtenida previamente para la función de sistema del filtro digital, que es equivalente a la -cadena.
Encontremos el algoritmo de filtrado digital correspondiente a la función del sistema (4.10). Para ello, resolvemos la ecuación (4.9) con respecto a
Un circuito equivalente de este algoritmo se muestra en la Fig. 4.6. En comparación con el filtro no recursivo (ver Fig. 4.5), aquí se ha agregado una especie de "bucle de retroalimentación", lo que significa que los valores de la señal de salida se utilizan en los siguientes

Figura: 4.6. Esquema de un filtro digital recursivo similar a una cadena
cálculos. Los filtros de este tipo se denominan recursivos.
El algoritmo (4.11) corresponde a un filtro que es completamente equivalente al filtro no recursivo previamente considerado. Pero para determinar un valor de la señal de salida usando el algoritmo de filtro no recursivo (4.4), se requiere realizar operaciones, y cuando se usa el algoritmo de filtro recursivo (4.11), solo se requieren dos operaciones. Ésta es la principal ventaja de los filtros recursivos. Además, los filtros recursivos permiten procesar la señal con mayor precisión, ya que permiten una implementación más correcta de la respuesta al impulso sin descartar su "cola". Los filtros recursivos le permiten implementar algoritmos que generalmente no son posibles con filtros no recursivos. Por ejemplo, con un filtro que funciona según el esquema de la Fig. 4.6, es, en esencia, un acumulador-integrador ideal y tiene una respuesta de impulso de la forma Un filtro con tal característica no se puede implementar en un circuito no recursivo.
Los ejemplos considerados muestran que no tiene sentido aplicar algoritmos no recursivos para crear filtros digitales con una respuesta de impulso larga. En estos casos, tiene más sentido utilizar filtros recursivos.
El campo de aplicación de los algoritmos no recursivos es la implementación de filtros digitales con un número reducido de términos respuesta a impulso. Un ejemplo es un diferenciador simple cuya señal de salida es igual al incremento de la señal de entrada:
El diagrama de dicho filtro digital se muestra en la Fig. 4.7.

Figura: 4.7. Diagrama del diferenciador digital más simple
Considere ahora un filtro digital general, que se describe mediante la ecuación
Esta ecuación se puede considerar como una ecuación de diferencia de orden y como un algoritmo de filtrado digital, si la reescribimos de manera diferente, es decir

Figura: 4.8. Circuito de filtro de orden digital recursivo
El algoritmo (4.13) corresponde al esquema que se muestra en la Fig. 4.8. Encontremos la función del sistema de dicho filtro. Para hacer esto, aplique a la ecuación -transformación:
La expresión (4.14) permite establecer una conexión entre las oscilaciones de los elementos del circuito de filtrado y la función del sistema. Los coeficientes en el numerador de la función del sistema determinan los valores de los coeficientes en
(en la parte no recursiva del filtro) y los coeficientes en el denominador definen la parte recursiva del filtro.
48 filtros digitales con respuesta de impulso finita. Cálculo de filtros de cue.
Filtro de respuesta de impulso finito (Filtro no recursivo, Filtro FIR) o FIR-filter (FIR abreviatura para respuesta de impulso finita) - uno de los tipos de filtros digitales lineales, un rasgo característico del cual es su respuesta de impulso limitada en el tiempo (a partir de algún momento se vuelve exactamente cero). Dicho filtro también se denomina no recursivo debido a la falta de retroalimentación. El denominador de la función de transferencia de dicho filtro es una cierta constante.
Ecuación de diferencia que describe la relación entre las señales de entrada y salida del filtro: donde PAGS- orden de filtrado, x(norte) - señal de entrada, y(norte) es la señal de salida, y segundo yo - coeficientes de filtrado. En otras palabras, el valor de cualquier muestra de la señal de salida está determinado por la suma de los valores escalados. PAGSmuestras anteriores. Se puede decir de otra manera: el valor de la salida del filtro en cualquier momento es el valor de la respuesta al valor instantáneo de la entrada y la suma de todas las respuestas que disminuyen gradualmente. PAGSmuestras de señal anteriores que aún afectan la salida (después PAGS-recuentos, la función transitoria de impulso se vuelve igual a cero, como ya se mencionó, por lo PAGSth también se vuelve igual a cero). Escribamos la ecuación anterior en una forma más amplia:

Para encontrar el núcleo del filtro, ponga
x(norte) = δ( norte)
donde δ ( norte) es una función delta. Entonces, la respuesta al impulso del filtro FIR se puede escribir como:

La transformada Z de la respuesta al impulso nos da la función de transferencia del filtro FIR:

] Propiedades
Un filtro FIR tiene una serie de propiedades útiles que a veces lo hacen más preferible de usar que un filtro IIR. Éstos son algunos de ellos:
Los filtros FIR son robustos.
Los filtros FIR no requieren retroalimentación cuando se implementan.
La fase de los filtros FIR se puede hacer lineal
Filtro FIR de forma directa
Los filtros FIR se pueden implementar usando tres elementos: un multiplicador, un sumador y una unidad de retardo. La variante que se muestra en la figura es una implementación directa de los filtros FIR de tipo 1.

Implementación de filtro FIR de forma directa
Programa de muestra
El siguiente es un programa de filtro FIR de ejemplo escrito en C:
/ * Filtro FIR para 128 tomas * /
flotar fir_filter (entrada flotante)
muestra flotante estática;
acc \u003d 0.0f; /* Batería */
/ * Multiplicación y acumulación * /
para (i \u003d 0; i< 128; i++) {
acc + \u003d (h [i] * muestra [i]);
/ * Salida * /
/ * Compensación de la señal retardada * /
para (i \u003d 127; i\u003e 0; i--)
muestra [i] \u003d muestra;
49 Suavizado de datos. Mover el promedio.
50 Suavizado de datos. Alisado con parábolas.
51 Suavizado de datos. Spencer alisando.
52 Suavizado de datos. Filtrado mediano.
Promedio de movimiento, suavizado por conejos, suavizado de Spencer, filtrado de mediana
Al desarrollar métodos para determinar los parámetros de procesos físicos que cambian lentamente en el tiempo, una tarea importante es eliminar la influencia de los efectos de ruido o interferencias aleatorias que se superponen a la señal procesada recibida en la salida del convertidor primario.
Para eliminar este efecto, puede aplicar suavizado de datos. Una de las formas más sencillas de hacer esto es el promedio aritmético. Cuando se aplica, cada valor de una función discreta (matriz de datos procesados) se calcula de acuerdo con la expresión:
donde es el número de puntos para el promedio aritmético (entero impar);
Valor de función pasado antes del procesamiento;
También existen otros métodos de suavizado bastante efectivos, por ejemplo, mediante parábolas de segundo grado en cinco, siete, nueve y once puntos de acuerdo con las expresiones:
o parábolas de cuarto grado a los siete, nueve, once y trece puntos:
En aplicaciones prácticas, otros métodos efectivos dan buenos resultados, por ejemplo, alisado Spencer de 15 puntos:
Sustituyendo un exponente complejo en estas expresiones, donde se puede determinar la función de transferencia de la transformación correspondiente.
Para promediar aritmética
La expresión entre paréntesis es una progresión geométrica con denominador, por lo tanto, esta expresión se puede representar como:
 .
.
Esta fórmula representa la característica de transferencia del filtro de paso bajo y puede verse en ella que cuantos más términos estén involucrados en el promedio, mayor será la supresión de los componentes de ruido de alta frecuencia en la señal (ver Figura 6.1).
Sin embargo, el concepto de frecuencia cuando se procesan tendencias de tiempo difiere del concepto análogo cuando se procesan señales. Esto se debe a que a la hora de estudiar las tendencias temporales lo que interesa no es su composición de frecuencias, sino el tipo de cambio (aumento, disminución, constancia, ciclicidad, etc.).
El uso de los llamados algoritmos heurísticos también es bastante efectivo para suavizar los datos.
Uno de ellos es el filtrado medio. En el curso de su implementación en una ventana de tiempo deslizante de dimensión, donde un número entero es un número impar, el elemento central es reemplazado por el elemento central de la secuencia, que son ordenados, en orden ascendente de valores, elementos de la matriz de datos de la señal suavizada que caen en la ventana de tiempo. La ventaja del filtrado medio es la capacidad de eliminar el ruido de impulso, cuya duración no excede, prácticamente sin distorsionar las señales que cambian suavemente. Este método de supresión de ruido no tiene una justificación matemática rigurosa, pero la sencillez de los cálculos y la eficacia de los resultados obtenidos han propiciado su uso generalizado.

Figura 6.1 - Gráficos de características de transferencia
operaciones de promedio aritmético para m \u003d 5, 7, 9, 11
Otro algoritmo de suavizado interesante es el promedio de la mediana. Su esencia es la siguiente. En una ventana de tiempo deslizante, las dimensiones (- un número entero impar), los elementos de la matriz de datos se ordenan en orden ascendente, y luego el primer y último elemento se eliminan de la secuencia ordenada (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Este método le permite suprimir los impulsos y las interferencias de radiofrecuencia, así como lograr un buen suavizado de la señal.
| " |