ყველაფერი იქიდან დაიწყო, რომ ჩემი მეგობრის მეგობრის მეგობარს დახმარება სწორედ ამ ფილტრებისთვის სჭირდებოდა. ჯედას გზების საშუალებით, ამ თემაზე ჭორებმა მიაღწია, მე გამოვწერე კომენტარი ბმულზე განთავსებულ კომენტარზე. როგორც ჩანს, ეს დაეხმარა. იმედი მაქვს.
ამ ამბავმა გაუღვიძა მოგონებები მესამე კურსზე, ან რამე სხვაზე, როდესაც DSP ჩავაბარე და შთააგონა სტატიის დაწერა ყველასთვის, ვინც დაინტერესებულია თუ როგორ მუშაობს ციფრული ფილტრები, მაგრამ ბუნებრივად მათ აშინებთ უხამსი ფორმულები და ფსიქოდელიური ნახატები (მე უკვე მე არ ვსაუბრობ სახელმძღვანელოებზე).
საერთოდ, ჩემი გამოცდილებით, სახელმძღვანელოებთან დაკავშირებული ვითარება აღწერილია ცნობილი ფრაზით იმის შესახებ, რომ ხეების უკან ტყე არ ჩანს. და ეს უნდა ითქვას, რომ როდესაც ისინი პირდაპირ შეგაშინებენ Z- ტრანსფორმაციისა და პოლინომების დაყოფის ფორმულებით, რომლებიც ხშირად ორ დაფაზე მეტია, თემისადმი ინტერესი ძალიან სწრაფად ქრება. ჩვენ დავიწყებთ მარტივს, რადგან სულაც არ არის საჭირო გრძელი რთული გამოთქმების დახატვა იმის გასაგებად, თუ რა ხდება.
პირველ რიგში, რამდენიმე მარტივი ძირითადი ცნება.
1. იმპულსის პასუხი.
ვთქვათ, გვაქვს ყუთი ოთხი პინით. წარმოდგენა არ გვაქვს რა არის შიგნით, მაგრამ დანამდვილებით ვიცით, რომ ორი მარცხენა ქინძი არის შესასვლელი, ხოლო ორი მარჯვენა ქინძისთავი არის გასასვლელი. შევეცადოთ გამოვიყენოთ ძალიან დიდი ამპლიტუდის ძალიან მოკლე პულსი და ვნახოთ რა ხდება გამომავალზე. რატომ, სულ ერთია, რომ ამ ოთხპოლუსის შიგნით - გაუგებარია, რადგან გაუგებარია მისი აღწერა, ასე რომ, სულ მცირე, ჩვენ მაინც ვნახავთ რამეს.
აქ უნდა ითქვას, რომ დიდი (ზოგადად ლაპარაკით, უსასრულოდ მოკლე) დიდი (ზოგადად საუბარი, უსასრულო) ამპლიტუდის მოკლე (ზოგადად ლაპარაკი, უსასრულო) ამპლიტუდის თეორიულად დელტას ფუნქციას უწოდებენ. სხვათა შორის, სასაცილო ის არის, რომ ამის განუყოფელი ნაწილია დაუსრულებელი ფუნქცია უდრის ერთს. ასეთია ნორმალიზაცია.
ასე რომ, რასაც ჩვენ ვნახეთ ოთხი პორტიანი ქსელის გამოსასვლელში, დელტა ფუნქციის შეყვანისას, ეწოდება იმპულსური პასუხი ეს ოთხპოლუსიანი. ჯერჯერობით, გაუგებარია, როგორ დაგვეხმარება, მაგრამ ახლა უბრალოდ გავიხსენოთ შედეგი და გადავიდეთ შემდეგ საინტერესო კონცეფციაზე.
2. კონვოლუცია.
მოკლედ, კონვოლუცია არის მათემატიკური ოპერაცია, რომელიც ამცირებს ფუნქციების პროდუქტის ინტეგრირებას:
![]()
ეს მითითებულია, როგორც ხედავთ, ვარსკვლავით. თქვენ ასევე ხედავთ, რომ კონვოლუციის დროს, ერთი ფუნქცია მიიღება მისი "პირდაპირი" თანმიმდევრობით, ხოლო მეორეს "უკან წინა" გადავცემთ. რა თქმა უნდა, კაცობრიობისთვის უფრო ღირებულ დისკრეტულ შემთხვევაში, კონვოლუცია, ისევე როგორც ნებისმიერი ინტეგრალი, გადადის ჯამში:

ეს, როგორც ჩანს, ერთგვარი მოსაწყენი მათემატიკური აბსტრაქციაა. თუმცა, სინამდვილეში, კონვოლუცია ალბათ ამ სამყაროს ყველაზე ჯადოსნური ფენომენია, რაც გასაკვირია მხოლოდ სამყაროში ადამიანის დაბადებით, მხოლოდ იმ განსხვავებით, რომ იქ, სადაც ბავშვები მოდიან, ადამიანების უმეტესობა სულ მცირე თვრამეტი წლის ასაკში სწავლობს, ხოლო ამის შესახებ, რა არის კონვოლუცია და რამდენად სასარგებლო და საოცარი, მსოფლიოს მოსახლეობის უზარმაზარ ნაწილს საერთოდ არ აქვს წარმოდგენა მთელი ცხოვრების განმავლობაში.
ამ ოპერაციის სიმძლავრე იმაში მდგომარეობს, რომ თუ f არის თვითნებური შეყვანის სიგნალი, და g არის ოთხ პორტიანი ქსელის იმპულსური პასუხი, მაშინ ამ ორი ფუნქციის კონვოლუციის შედეგი იქნება მსგავსი, რასაც მივიღებთ f სიგნალის გავლით ამ ოთხ პორტიან ქსელში.
ანუ იმპულსური პასუხი არის კვადროპოლის ყველა თვისების სრული შემადგენლობა შეყვანის მოქმედებასთან მიმართებაში და მასთან შეყვანის სიგნალის კონვოლუცია საშუალებას გაძლევთ აღადგინოთ შესაბამისი გამომავალი სიგნალი. რაც შეეხება მე, ეს უბრალოდ საოცარია!
3. ფილტრები.
იმპულსის რეაგირებისა და კონვოლუციის საშუალებით ბევრი რამის გაკეთება შეგიძლიათ. მაგალითად, თუ სიგნალი ხმამაღალია, შეგიძლიათ მოაწყოთ რევერბი, ექო, გუნდი, ფლანგერი და მრავალი სხვა; შეიძლება დიფერენცირებული და ინტეგრირებული იყოს ... ზოგადად, თქვენ შეგიძლიათ შექმნათ ყველაფერი. ახლა ჩვენთვის ყველაზე მნიშვნელოვანია ის, რომ, რა თქმა უნდა, კონვოლუციის გამოყენებით, ფილტრები ისეთივე ადვილად მიიღება.
ციფრული ფილტრი თავისთავად არის შეყვანის სიგნალის კონვოლუცია იმპულსის რეაქციით, რომელიც სასურველი ფილტრის შესაბამისია.
მაგრამ, რა თქმა უნდა, იმპულსური პასუხი როგორმე უნდა მივიღოთ. ჩვენ, რა თქმა უნდა, უკვე მივხვდით, თუ როგორ უნდა გავზომოთ ზემოთ, მაგრამ ასეთ ამოცანას აზრი არ აქვს - თუ ფილტრი უკვე აწყობილი გვაქვს, სხვაგან რატომ უნდა გავზომოთ რამე, შეგიძლიათ გამოიყენოთ ისე, როგორც არის. გარდა ამისა, ციფრული ფილტრების ყველაზე მნიშვნელოვანი მნიშვნელობა იმაშია, რომ მათ შეიძლება ჰქონდეთ მახასიათებლები, რომლებიც რეალობაში მიუღწეველია (ან ძალზე ძნელი მისაღწევია) - მაგალითად, ხაზოვანი ფაზა. ასე რომ, გაზომვის საშუალება საერთოდ არ არსებობს, უბრალოდ უნდა დაითვალოთ.
4. იმპულსური პასუხის მიღება.
ამ ეტაპზე, ამ პუბლიკაციების უმეტესობაში, ავტორები იწყებენ მკითხველს Z- გარდაქმნებისა და წილადების ფრაქციების მთების გადაყრას მკითხველს, რაც მას აბსოლუტურად არეულობს. ამას არ გავაკეთებ, უბრალოდ მოკლედ ავუხსნი რისთვის არის ეს ყველაფერი და რატომ არ არის ეს საჭირო პროგრესული საზოგადოებისთვის პრაქტიკაში.
დავუშვათ, რომ გავიგეთ, რა გვინდა ფილტრისგან და გავაკეთეთ განტოლება, რომელიც მას აღწერს. გარდა ამისა, იმპულსური პასუხის მოსაძებნად შეგიძლიათ დელტა ფუნქცია ჩაანაცვლოთ მიღებულ განტოლებაში და მიიღოთ სასურველი. ერთადერთი პრობლემა ის არის, თუ როგორ უნდა გავაკეთოთ ეს, რადგან დელტა დროულად ფუნქციონირებს დაახლოებითმე -6 არეალს ეშმაკური სისტემა ადგენს და საერთოდ, ყველანაირი უსასრულობაა. ამ ეტაპზე ყველაფერი საშინლად რთული აღმოჩნდა.
აქ ეს ხდება და მათ ახსოვთ, რომ არსებობს ლაპლასის გარდაქმნა. თავისთავად, ეს არ არის ქიშმიშის ფუნტი. ერთადერთი მიზეზი იმისა, რომ ეს რადიოტექნიკაში აიტანება, არის ზუსტად ის ფაქტი, რომ არგუმენტის სივრცეში, რომლის გადასვლაც არის ეს ტრანსფორმაცია, ზოგი რამ მართლაც მარტივდება. კერძოდ, ძალიან დელტა ფუნქცია, რამაც ამდენი უბედურება მოგვცა დროის სფეროში, ძალიან მარტივად არის გამოხატული - აქ ის მხოლოდ ერთეულია!
Z- გარდაქმნა (იგივე ლორანის გარდაქმნა) ლაპლასის გარდაქმნის დისკრეტული ვარიანტია.
ანუ, ლაპლასის გარდაქმნის (ან საჭიროების შემთხვევაში Z- გარდაქმნის) გამოყენება სასურველი ფილტრის აღმწერი ფუნქციისთვის, მისი ჩანაცვლება შედეგად მიღებულში და მისი გარდაქმნა, მივიღებთ იმპულსურ პასუხს. მარტივად ჟღერს, ყველას შეუძლია სცადოს. მე ამას არ გავრისკავ, რადგან, როგორც უკვე აღვნიშნეთ, ლაპლასის გარდაქმნა მკაცრია, განსაკუთრებით პირიქით. მოდით, ეს უკანასკნელ საშუალებად დავტოვოთ და ჩვენ თვითონ ვეძებთ უფრო მარტივ გზებს იმის მისაღებად, რასაც ვეძებთ. რამდენიმე მათგანია.
პირველ რიგში, შეგვიძლია გავიხსენოთ ბუნების კიდევ ერთი საოცარი ფაქტი - ამპლიტუდა-სიხშირე და იმპულსის მახასიათებლები ერთმანეთთან დაკავშირებულია ფურიეს კეთილი და ნაცნობი ტრანსფორმაციით. ეს ნიშნავს, რომ ჩვენ შეგვიძლია ნებისმიერი სიხშირის რეაგირება მოვახდინოთ ჩვენს გემოვნებაზე, ავიღოთ მისგან შებრუნებული ფურიეს გარდაქმნა (თუმცა უწყვეტი, თუნდაც დისკრეტული) და მივიღოთ იმპულსური პასუხი სისტემისგან, რომელიც ახორციელებს მას. უბრალოდ გასაოცარია!
ამასთან, აქ პრობლემა არ გაკეთდება. პირველი, იმპულსური პასუხი, რომელიც ჩვენ მივიღეთ, სავარაუდოდ უსასრულო იქნება (მე არ განვმარტავ იმის ახსნას, თუ რატომ; ასე მუშაობს სამყარო), ასე რომ, ჩვენ მოგვიწევს ნებაყოფლობითი გადაწყვეტილება მივიღოთ მისი შეწყვეტის შესახებ გარკვეულ მომენტში (ნულის ტოლი ამ წერტილის მიღმა). მაგრამ ეს ასე არ იმუშავებს - ამის შედეგად, როგორც თქვენ მოელოდით, მოხდება გაანგარიშებული ფილტრის სიხშირეზე რეაგირების დამახინჯება - გახდება ტალღოვანი და სიხშირის შემცირება ბუნდოვანია.
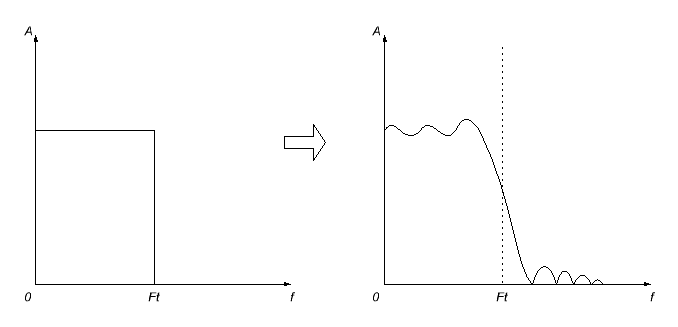
ამ ეფექტების შემცირების მიზნით, შემცირების იმპულსის რეაგირებისთვის გამოიყენება გამარტივების ფანჯრის სხვადასხვა ფუნქციები. შედეგად, სიხშირეზე რეაგირება, როგორც წესი, კიდევ უფრო ბუნდოვანია, მაგრამ უსიამოვნო (განსაკუთრებით გამტარ ზოლში) რხევები ქრება. 
სინამდვილეში, ასეთი დამუშავების შემდეგ, ჩვენ ვიღებთ ოპერაციულ იმპულსურ რეაგირებას და შეგვიძლია ციფრული ფილტრის შექმნა.
გაანგარიშების მეორე მეთოდი კიდევ უფრო მარტივია - ყველაზე პოპულარული ფილტრების იმპულსური პასუხები დიდი ხანია ჩვენთვის ანალიტიკური ფორმით არის გამოხატული. ის რჩება მხოლოდ თქვენი მნიშვნელობების ჩანაცვლება და შედეგის შესაბამისად ფანჯრის ფუნქციის გამოყენება. ასე რომ თქვენ არც კი გჭირდებათ რაიმე გარდაქმნების დათვლა.
და, რა თქმა უნდა, თუ მიზანი არის კონკრეტული სქემის ქცევის მიბაძვა, შეგიძლიათ მიიღოთ იმპულსის პასუხი სიმულატორში:

აქ მე მივმართე პულსი 100500 ვოლტ (დიახ, 100,5 კვ) ხანგრძლივობით 1 მკმ RC ჩართვისთვის და მივიღე მისი იმპულსური პასუხი. ცხადია, რომ სინამდვილეში ამის გაკეთება არ შეიძლება, მაგრამ სიმულატორში ეს მეთოდი, როგორც ხედავთ, შესანიშნავად მუშაობს.
5. შენიშვნები.
ზემოხსენებული იმპულსური პასუხის შემცირების შესახებ, რა თქმა უნდა, ეხებოდა ე.წ. სასრული იმპულსის რეაგირების (FIR / FIR) ფილტრები. მათ აქვთ მრავალი ღირებული თვისება, ხაზოვანი ფაზის ჩათვლით (იმპულსის რეაგირების გარკვეულ პირობებში), რაც არ იძლევა სიგნალის დამახინჯებას ფილტრაციის დროს, ასევე აბსოლუტურ სტაბილურობას. ასევე არსებობს უსასრულო იმპულსის რეაგირების მქონე ფილტრები (IIR / IIR ფილტრები). ისინი ნაკლებად ინტენსიურია რესურსებით გათვლებით, მაგრამ მათ აღარ აქვთ ჩამოთვლილი უპირატესობები.
შემდეგ სტატიაში, იმედი მაქვს, პრაქტიკული ციფრული ფილტრის განხორციელების მარტივი მაგალითი გაჩვენებთ.
ლექცია ნომერი 10
სასრული იმპულსის რეაგირების ციფრული ფილტრები
ფიზიკურად რეალიზებადი სასრული იმპულსის რეაგირების ფილტრის (FIR ფილტრი) გადაცემის ფუნქცია შეიძლება იყოს წარმოდგენილი
(10.1).
გამოხატვის (10.1) შეცვლისას ვიღებთ FIR ფილტრის სიხშირეზე რეაგირებას სახით
![]() (10.2),
(10.2),
სად ![]() - ამპლიტუდა-სიხშირის მახასიათებელი (AFC) ფილტრი,
- ამპლიტუდა-სიხშირის მახასიათებელი (AFC) ფილტრი,
![]() - ფაზის სიხშირის მახასიათებელი (PFC) ფილტრი
- ფაზის სიხშირის მახასიათებელი (PFC) ფილტრი
ფაზის დაგვიანება ფილტრი განისაზღვრება, როგორც
![]() (10.3).
(10.3).
ჯგუფური დაგვიანება ფილტრი განისაზღვრება, როგორც
![]() (10.4).
(10.4).
FIR ფილტრების გამორჩეული თვისება არის მუდმივი ფაზის და ჯგუფური შეფერხებების განხორციელების შესაძლებლობა, ე.ი. ხაზოვანი ფაზის პასუხი
(10.5),
სადაც ა მუდმივია. თუ ეს პირობა დაკმაყოფილებულია, ფილტრში გამავალი სიგნალი არ ამახინჯებს მის ფორმას.
იმ პირობების გამოსაყვანად, რომლებიც ხაზოვან ფაზურ რეაგირებას უზრუნველყოფს, ჩვენ ვწერთ FIR ფილტრის სიხშირეზე რეაგირებას, გათვალისწინებით (10.5)
![]() (10.6).
(10.6).
ამ თანასწორობის რეალური და წარმოსახვითი ნაწილების გათანაბრება, მივიღებთ
 (10.7).
(10.7).
მეორე განტოლების დაყოფით პირველზე, მივიღებთ
 (10.8).
(10.8).
დაბოლოს, შეგიძლიათ დაწეროთ
 (10.9).
(10.9).
ამ განტოლებას აქვს ორი ამოხსნა. პირველია \u003d 0 განტოლებას შეესაბამება
 (10.10).
(10.10).
ამ განტოლებას აქვს უნიკალური ამოხსნა, რომელიც შეესაბამება თვითნებურსh (0) (sin (0) \u003d 0) და h (n) \u003d 0 n– სთვის \u003e 0 ეს ამოხსნა შეესაბამება ფილტრს, რომლის იმპულსურ რეაქციას აქვს თავდაპირველი ერთი ნულოვანი რაოდენობა. ასეთი ფილტრი პრაქტიკულ ინტერესს არ წარმოადგენს.
მოდით ვიპოვნოთ სხვა გამოსავალი. ამ შემთხვევაში, მრიცხველების და მნიშვნელების ჯვარედინად გამრავლება (10.8) -ში, მივიღებთ
(10.11).
აქედან ჩვენ გვაქვს
![]() (10.12).
(10.12).
რადგან ამ განტოლებას აქვს ფურიეს სერიის ფორმა, მისი ამოხსნა, თუ ის არსებობს, უნიკალურია.
ადვილი მისახვედრია, რომ ამ განტოლების ამოხსნა უნდა აკმაყოფილებდეს პირობებს
(10.13),
(10.14).
(10.13) პირობიდან გამომდინარეობს, რომ თითოეული ფილტრის შეკვეთისთვისნ მხოლოდ ერთი ფაზის დაგვიანებააა , რომლის დროსაც შესაძლებელია ფაზის რეაგირების მკაცრი სწორხაზოვნების მიღწევა. (10.14) მდგომარეობიდან გამომდინარეობს, რომ ფილტრის იმპულსური რეაქცია სიმეტრიული უნდა იყოს წერტილისთვის უცნაურინ და ინტერვალის შუა წერტილთან შედარებით (სურათი 10.1).
 |
ასეთი ფილტრის სიხშირეზე რეაგირება (უცნაურიან ) შეიძლება დაიწეროს როგორც
(10.15).
ჩანაცვლება მეორე ოდენობითm \u003d N -1- n, მივიღებთ
(10.16).
მას შემდეგ, რაც h (n) \u003d h (N -1- n) ), მაშინ ორი ჯამი შეიძლება გაერთიანდეს
 (10.17).
(10.17).
შემცვლელი, მივიღებთ
(10.18).
თუ აღვნიშნავთ
 (10.19),
(10.19),
შემდეგ შეგვიძლია საბოლოოდ დავწეროთ
 (10.20).
(10.20).
ამრიგად, ხაზოვანი ფაზის რეაგირების მქონე ფილტრისთვის გვაქვს
 (10.21).
(10.21).
იმ შემთხვევაშიც კინ ანალოგიურად გვექნება
 (10.22).
(10.22).
ჩანაცვლება მეორე ჯამში, მივიღებთ
 (10.23).
(10.23).
ჩანაცვლების გაკეთება, მივიღებთ
(10.24).
დანიშვნის გზით
![]() (10.25),
(10.25),
საბოლოოდ ექნება
 (10.26).
(10.26).
ამრიგად, FIR ფილტრისთვის წრფივი ფაზის რეაგირებით და თანაბარი თანმიმდევრობითN შეიძლება დაიწეროს
 (10.27).
(10.27).
შემდეგში, მარტივად, ჩვენ განვიხილავთ მხოლოდ უცნაური ბრძანების მქონე ფილტრებს.
ფილტრის გადაცემის ფუნქციის სინთეზის დროს, საწყისი პარამეტრები, როგორც წესი, მოთხოვნებია სიხშირის რეაგირებისთვის. FIR ფილტრების სინთეზის მრავალი მეთოდი არსებობს. მოდით განვიხილოთ ზოგიერთი მათგანი.
ვინაიდან ნებისმიერი ციფრული ფილტრის სიხშირეზე რეაგირება სიხშირის პერიოდული ფუნქციაა, ის შეიძლება წარმოდგენილი იყოს როგორც ფურიეს სერია
![]() (10.28),
(10.28),
სადაც არის ფურიეს სერიის კოეფიციენტები
 (10.29).
(10.29).
ჩანს, რომ ფურიეს სერიის კოეფიციენტებით (ნ ) ემთხვევა ფილტრის იმპულსის რეაგირების კოეფიციენტებს. ამიტომ, თუ ფილტრის საჭირო სიხშირის რეაგირების ანალიტიკური აღწერა ცნობილია, შესაძლებელია მარტივად განისაზღვროს მისგან იმპულსის რეაგირების კოეფიციენტები და მათგან ფილტრის გადაცემის ფუნქცია. ამასთან, პრაქტიკაში ეს შეუძლებელია, რადგან ასეთი ფილტრის იმპულსურ რეაგირებას უსასრულო სიგრძე აქვს. გარდა ამისა, ასეთი ფილტრი ფიზიკურად ვერ ხვდება, რადგან იმპულსური რეაქცია იწყება -¥ , და არცერთი სასრული შეფერხება არ გახდის ამ ფილტრის ფიზიკურად რეალიზებას.
მოცემული სიხშირის რეაქციის დაახლოების FIR ფილტრის მიღების ერთ-ერთი შესაძლო მეთოდია უსასრულო ფურიეს სერიისა და ფილტრის იმპულსური პასუხის შემცირება, ვთქვათ რომh (n) \u003d 0 ამისთვის. შემდეგ
 (10.30).
(10.30).
გადაცემის ფუნქციის ფიზიკური მიზანშეწონილობაH (ზ ) გამრავლებით მიიღწევაH (z) ჩართულია.
 (10.31),
(10.31),
სად
(10.32).
გადაცემის ფუნქციის ამ მოდიფიკაციით, ფილტრის ამპლიტუდის მახასიათებელი არ იცვლება და ჯგუფის დაგვიანება იზრდება მუდმივი მნიშვნელობით.
მაგალითად, მოდით გამოვთვალოთ დაბალი გამშვები FIR ფილტრი ფორმის სიხშირის რეაგირებით
 (10.33).
(10.33).
(10.29) შესაბამისად, ფილტრის იმპულსის რეაგირების კოეფიციენტები აღწერილია გამოხატულებით
 (10.34).
(10.34).
ახლა (10.31) –დან შეგიძლიათ მიიღოთ გამოხატვა გადაცემის ფუნქციისთვის
 (10.35),
(10.35),
სად
(10.36).
გამოთვლილი ფილტრის ამპლიტუდის მახასიათებლები სხვადასხვან წარმოდგენილია ნახაზზე 10.2.

სურათი 10.2
ტალღა გასასვლელ ზოლში და გაჩერების ზონაში ხდება ფურიეს სერიის ნელი კონვერგენციის გამო, რაც, თავის მხრივ, განპირობებულია ფუნქციის შეწყვეტის გამო გამტარ ზოლის გათიშვის სიხშირეზე. ეს ტალღები ცნობილია, როგორც გიბსის ტალღა.
სურათი 10.2 გვიჩვენებს, რომ იზრდებან ტალღური სიხშირე იზრდება და ამპლიტუდა მცირდება როგორც ქვედა, ასევე მაღალ სიხშირეებზე. ამასთან, გასასვლელ ზოლში ბოლო ტალღის ამპლიტუდა და გაჩერების ზოლში პირველი ტალღა პრაქტიკულად უცვლელი რჩება. პრაქტიკაში, ასეთი ეფექტები ხშირად არასასურველია, რაც მოითხოვს გიბსის პულსაციების შემცირების გზების მოძებნას.
შემცირებული იმპულსის პასუხით (ნ ) შეიძლება წარმოდგენილი იყოს როგორც საჭირო უსასრულო იმპულსის რეაგირების პროდუქტი და ზოგიერთი ფანჯრის ფუნქციები w (n) სიგრძის n (სურათი 10.3).
![]() (10.37).
(10.37).
 |
ფურიეს სერიის მარტივი შეკვეცის განხილვის შემთხვევაში, ჩვენ ვიყენებთ მართკუთხა ფანჯარა
 (10.38).
(10.38).
ამ შემთხვევაში, ფილტრის სიხშირეზე რეაგირება შეიძლება წარმოდგენილი იყოს როგორც რთული კონვოლუცია
 (10.39).
(10.39).
ეს ნიშნავს, რომ ეს იქნება საჭირო მახასიათებლის "ბუნდოვანი" ვარიანტი.
პრობლემა შემცირდება ფანჯრის ფუნქციების პოვნაში, რომელსაც შეუძლია შეამციროს გიბსის ტალღა იმავე ფილტრის არჩევითობით. ამისათვის თქვენ ჯერ უნდა შეისწავლოთ ფანჯრის ფუნქციის თვისებები მართკუთხა ფანჯრის მაგალითის გამოყენებით.
მართკუთხა ფანჯრის ფუნქციის სპექტრი შეიძლება დაიწეროს როგორც
 (10.40).
(10.40).
მართკუთხა ფანჯრის ფუნქციის სპექტრი ნაჩვენებია ნახაზზე 10.4.

სურათი 10.4
მას შემდეგ, რაც, სპექტრის ძირითადი წილის სიგანე აღმოჩნდება.
გვერდითი წილის არსებობა ფანჯრის ფუნქციის სპექტრში იწვევს გიბსის ტალღების გაზრდას ფილტრის სიხშირეზე. გასასვლელ ზოლში მცირე ტალღის მისაღებად და საცობში დიდი შესუსტების მისაღებად აუცილებელია, რომ გვერდითი წნულებით შემოზღუდული ფართობი იყოს მთავარი წილით შემოზღუდული არეალის მცირე ნაწილი.
თავის მხრივ, ძირითადი წილის სიგანე განსაზღვრავს მიღებული ფილტრის გარდამავალი ზონის სიგანეს. ფილტრის მაღალი შერჩევისთვის, მთავარი წილის სიგანე უნდა იყოს რაც შეიძლება მცირე. როგორც ზემოდან ჩანს, მთავარი წილის სიგანე იკლებს ფილტრის რიგის ზრდასთან ერთად.
ამრიგად, შესაფერისი ფანჯრის ფუნქციების თვისებები შეიძლება ჩამოყალიბდეს შემდეგნაირად:
- ფანჯრის ფუნქცია უნდა შეიზღუდოს დროში;
- ფანჯრის ფუნქციის სპექტრი საუკეთესოდ უნდა მიუახლოვდეს სიხშირეზე შეზღუდულ ფუნქციას, ე.ი. აქვს მინიმალური ენერგია ძირითადი წილის გარეთ;
- ფანჯრის ფუნქციის სპექტრის მთავარი წილის სიგანე უნდა იყოს რაც შეიძლება ნაკლები.
ყველაზე ხშირად გამოყენებული ფანჯრის ფუნქციებია:
1. მართკუთხა ფანჯარა. ზემოთ განხილული.
2. ჩაქუჩის ფანჯარა.
 (10.41),
(10.41),
სად
როდესაც ამ ფანჯარას ჰენის ფანჯარა ეწოდება (დაკიდება).
3. შავკანიანი ფანჯარა.
 (10.42).
(10.42).
4. ბარტლეტის ფანჯარა.
 (10.43).
(10.43).
მითითებული ფანჯრის ფუნქციების გამოყენებით აშენებული ფილტრების მაჩვენებლები შეჯამებულია ცხრილში 10.1.
|
ფანჯარა |
მთავარი წილის სიგანე |
ტალღის ფაქტორი,% |
||
N \u003d 11 |
N \u003d 21 |
N \u003d 31 |
||
|
მართკუთხა |
22.34 |
21.89 |
21.80 |
|
|
ჰანინგი |
2.62 |
2.67 |
2.67 |
|
|
ჩაქუჩით |
1.47 |
0.93 |
0.82 |
|
|
Შავი კაცი |
0.08 |
0.12 |
0.12 |
|
ტალღური ფაქტორი განისაზღვრება, როგორც მაქსიმალური გვერდითი წილის ამპლიტუდის შეფარდება მთავარი ბორცვის ამპლიტუდისა და ფანჯრის ფუნქციის სპექტრში.
რეალური ფილტრების გაანგარიშებისას საჭირო ფილტრის შეკვეთის და ფანჯრის შესაფერისი ფუნქციის ასარჩევად შეგიძლიათ გამოიყენოთ მონაცემები ცხრილში 10.2.
|
გარდამავალი |
არათანაბარი გადაცემა (დბ) |
შესუსტება ბარიერები (დბ) |
|
|
მართკუთხა |
|||
|
ჰანინგი |
|||
|
ჩაქუჩით |
|||
|
Შავი კაცი |
როგორც ცხრილი 10.1-დან ჩანს, ფანჯრის ფუნქციის სპექტრში ტრიალების ფაქტორსა და ძირითადი წილის სიგანეს შორის არსებობს გარკვეული კავშირი. რაც უფრო დაბალია ტალღის კოეფიციენტი, მით უფრო ფართოა მთავარი წილის სიგანე და, შესაბამისად, გარდამავალი ზონა ფილტრის სიხშირის რეაქციაში. გასასვლელ ზოლში დაბალი ტალღის უზრუნველსაყოფად საჭიროა ფანჯრის არჩევა შესაფერისი ტალღური კოეფიციენტით და გარდამავალი ზონის საჭირო სიგანის გაზრდა ფილტრის N ბრძანებით.
ამ პრობლემის მოგვარება შესაძლებელია კაიზერის მიერ შემოთავაზებული ფანჯრის გამოყენებით. კაიზერის ფანჯრის ფუნქციას აქვს ფორმა
 (10.44),
(10.44),
სადაც a არის დამოუკიდებელი პარამეტრი, ![]() , I 0 არის პირველი ტიპის Bessel- ის ნულოვანი რიგის ფუნქცია, რომელიც განისაზღვრება გამოხატულებით
, I 0 არის პირველი ტიპის Bessel- ის ნულოვანი რიგის ფუნქცია, რომელიც განისაზღვრება გამოხატულებით
 (10.45).
(10.45).
კაიზერის ფანჯრის მიმზიდველი თვისება არის ტალღური კოეფიციენტის მცირე მნიშვნელობებიდან დიდი მნიშვნელობებში შეუფერხებლად შეცვლის შესაძლებლობა, როდესაც მხოლოდ ერთი პარამეტრი a შეიცვლება. ამ შემთხვევაში, რაც შეეხება სხვა ფანჯრის ფუნქციებს, ძირითადი წილის სიგანის კონტროლი შესაძლებელია ფილტრის ბრძანებით N.
რეალური ფილტრის შექმნისას დაყენებული ძირითადი პარამეტრებია:
გამტარობა - w p;
დაბრკოლების ზოლი - w a;
მაქსიმალური დასაშვები ტალღა გამტარ ზოლში - A p;
მინიმალური შესუსტება გაჩერების ზოლში - A a;
-შერჩევის სიხშირე -w ს
ეს პარამეტრები ილუსტრირებულია ნახაზზე 10.5. ამ შემთხვევაში, გამტარ ზოლში მაქსიმალური ტალღა განისაზღვრება, როგორც
![]() (10.46),
(10.46),
და მინიმალური შესუსტება გაჩერების ზოლში, როგორც
კაიზერის ფანჯრით ფილტრის გაანგარიშების შედარებით მარტივი პროცედურა მოიცავს შემდეგ ნაბიჯებს:
1. ფილტრის h (n) იმპულსური რეაქცია განისაზღვრება იმ პირობით, რომ სიხშირეზე რეაგირება იდეალურია
 (10.48),
(10.48),
სადაც (10.49).
2. პარამეტრი d შეირჩევა, როგორც
![]() (10.50),
(10.50),
სად  (10.51).
(10.51).
3. A a და A p ნამდვილი მნიშვნელობა გამოითვლება ფორმულებით (10.46), (10.47).
4. აირჩიეთ პარამეტრი a as
 (10.52).
(10.52).
5. აირჩიეთ პარამეტრი D, როგორც
 (10.53).
(10.53).
6. ფილტრის ბრძანების ყველაზე მცირე უცნაური მნიშვნელობა შეირჩევა პირობიდან
![]() (10.54),
(10.54),
 (10.57)
(10.57)
მიჰყვება იმას
ვინაიდან ფილტრის იმპულსის რეაგირების ნიმუშებია მისი გადაცემის ფუნქციის კოეფიციენტები, მდგომარეობა (10.59) ნიშნავს, რომ ფილტრის ყველა კოეფიციენტის კოდები შეიცავს მხოლოდ ფრაქციულ ნაწილს და ნიშნის ბიტს და არ შეიცავს მთელ ნაწილს.
ფილტრის კოეფიციენტების ფრაქციული ნაწილის ბიტების რაოდენობა განისაზღვრება ფილტრის გადაცემის ფუნქციის კვანტიზირებული კოეფიციენტებით დაკმაყოფილების პირობით, მითითებული მოთხოვნების მითითებით გადაცემის ფუნქციასთან კოეფიციენტების ზუსტი მნიშვნელობებით.
ფილტრის შეყვანის სიგნალების ნიმუშების აბსოლუტური მნიშვნელობები ჩვეულებრივ ნორმალიზდება ისე, რომ
თუ ანალიზი ხორციელდება FIR ფილტრისთვის ხაზოვანი ფაზის რეაქციით, მაშინ მისი გამომავალი სიგნალის გამოთვლის ალგორითმი შეიძლება იყოს შემდეგი:
სად არის ფილტრის კოეფიციენტები მომრგვალებული s k- ზე.
ეს ალგორითმი შეესაბამება ფილტრის 10.5 ნახაზზე ნაჩვენები ფილტრის ბლოკ დიაგრამას.
 |
ამ ალგორითმის განხორციელების ორი გზა არსებობს. პირველ შემთხვევაში, გამრავლების ყველა ოპერაცია ზუსტად შესრულებულია და არ ხდება პროდუქტების დამრგვალება. ამ შემთხვევაში, პროდუქტის სიტყვის სიგრძე უდრის s- ს + s k, სადაც s არის შეყვანის სიგნალის სიგანე, ხოლო s k არის ფილტრის კოეფიციენტების სიგანე. ამ შემთხვევაში, ნახაზი 10.5-ზე ნაჩვენები ფილტრის ბლოკ-დიაგრამა ზუსტად შეესაბამება რეალურ ფილტრს.
ალგორითმის განხორციელების მეორე გზით (10.61), გამრავლების ოპერაციის თითოეული შედეგი მრგვალდება, ე.ი. პროდუქტები გამოითვლება გარკვეული შეცდომით. ამ შემთხვევაში საჭიროა ალგორითმის (10.61) შეცვლა, რათა გაითვალისწინოთ შეცდომა პროდუქტის დამრგვალებით
თუ ფილტრის გამომავალი სიგნალის ნიმუშის გამოთვლა ხდება პირველი მეთოდით (პროდუქტების ზუსტი მნიშვნელობებით), მაშინ გამომავალი ხმაურის ვარიაცია განისაზღვრება, როგორც
![]() (10.66),
(10.66),
იმ დამოკიდებულია შეყვანის სიგნალის მრგვალი გამორთვის ხმაურის და ფილტრის კოეფიციენტების მნიშვნელობებზე. აქედან შეგიძლიათ იპოვოთ შეყვანის სიგნალის ბიტების საჭირო რაოდენობა, როგორც
 (10.67).
(10.67).
S და s k ცნობილი მნიშვნელობებიდან შეიძლება განისაზღვროს გამომავალი სიგნალის კოდის ფრაქციული ნაწილისთვის საჭირო ბიტების რაოდენობა, როგორც
თუ გამომავალი სიგნალის ნიმუშის გამოანგარიშება ხდება მეორე მეთოდის შესაბამისად, როდესაც თითოეული პროდუქტი მრგვალდება s ბიტამდე, მაშინ თითოეული მულტიპლიკატორის მიერ წარმოქმნილი დამრგვალების ხმაურის ვარიაცია შეიძლება გამოიხატოს პროდუქტის სიგანეზე,
გამოდის SN და გამოდის სიგნალი-ხმაურის შეფარდება ფილტრის გამოსასვლელთან. დეციბელებში შეყვანის სიგნალის დინამიური დიაპაზონის მნიშვნელობა განისაზღვრება შემდეგნაირად
![]() (10.74),
(10.74),
სადაც მაქსიმალური და მინ არის ფილტრის შეყვანის სიგნალის მაქსიმალური და მინიმალური ამპლიტუდები.
ფილტრის გამოსასვლელთან სიგნალისა და ხმაურის თანაფარდობა, გამოხატული დეციბელებით, განისაზღვრება, როგორც
![]() (10.75),
(10.75),
განსაზღვრავს ფილტრის გამოსასვლელი სინუსოიდალური სიგნალის სიმძლავრის ძირ-საშუალო კვადრატულ მნიშვნელობას A min ამპლიტუდით და
(10.77)
განსაზღვრავს ხმაურის ენერგიას ფილტრის გამოსასვლელში. (10.75) და (10.76) –დან A \u003d 1 ვიღებთ გამონათქვამს ფილტრის გამომავალი ხმაურის ვარიაციისთვის
![]() (10.78).
(10.78).
ფილტრის გამომავალი ხმაურის ვარიანტის ეს მნიშვნელობა შეიძლება გამოყენებულ იქნას ფილტრის შეყვანის და გამომავალი სიგნალების სიგანეების გამოსათვლელად.
მოდით განვიხილოთ ციფრული ფილტრების უმარტივესი - მუდმივი პარამეტრების მქონე ფილტრები.
შეყვანის სიგნალი მიეწოდება ციფრული ფილტრის შეყვანას ციფრული მნიშვნელობების თანმიმდევრობის სახით, ინტერვალით (ნახ. 4.1, ა). ციფრული ფილტრში ყოველი შემდეგი სიგნალის მნიშვნელობის მიღებისას გამოითვლება გამომავალი სიგნალის შემდეგი მნიშვნელობა.ანგარიშების ალგორითმები შეიძლება ძალიან მრავალფეროვანი იყოს; გაანგარიშების დროს, შეყვანის სიგნალის ბოლო მნიშვნელობის გარდა,
შემავალი და გამომავალი სიგნალების წინა მნიშვნელობები: ციფრული ფილტრის გამოსასვლელი სიგნალი ასევე რიცხვითი მნიშვნელობების თანმიმდევრობაა, შემდეგ ინტერვალით. ეს ინტერვალი იგივეა ციფრული სიგნალის დამუშავების მთელი მოწყობილობისთვის.

ფიგურა: 4.1. სიგნალი ციფრული ფილტრის შესასვლელთან და გამომავალთან
ამიტომ, თუ ციფრული ფილტრის შეყვანაზე გამოიყენება ერთი პულსის სახით უმარტივესი სიგნალი (ნახ .4.2, ა)
![]()
შემდეგ გამომავალზე მივიღებთ სიგნალს ციფრული მნიშვნელობების დისკრეტული თანმიმდევრობის სახით, შემდეგ ინტერვალით
ჩვეულებრივ ანალოგურ სქემებთან ანალოგიით, ამ საპასუხო სიგნალს დავარქვათ ფილტრის იმპულსის რეაგირება (ნახ. 4.2, ბ). ანალოგური წრის იმპულსური პასუხისგან განსხვავებით, ფუნქცია განზომილებიანია.

ფიგურა: 4.2. ერთი პულსი და ციფრული ფილტრის იმპულსის პასუხი
მოდით მივმართოთ თვითნებური დისკრეტული სიგნალი ფილტრის შეყვანაზე ნახ. 4.1, ა), რომელიც წარმოადგენს დისკრეტული მნიშვნელობების ერთობლიობას
ფილტრის გამოსასვლელზე პირველი ელემენტის მოქმედების შედეგად წარმოიქმნება თანმიმდევრობა გამრავლებული თანმიმდევრობაზე გამრავლებული და მარჯვნივ გადატანილი თანხით და ა.შ.

ამრიგად, გამომავალი სიგნალი განისაზღვრება, როგორც შეყვანის სიგნალის დისკრეტული კონვოლუცია და იმპულსის რეაგირება. ამ მხრივ, ციფრული ფილტრები ჩვეულებრივი სქემების მსგავსია, სადაც გამომავალი ტოლია შეყვანის და იმპულსის რეაგირების კონვოლუციის.
ფორმულა (4.1) არის ციფრული გაფილტვრის ალგორითმი. თუ ფილტრის იმპულსური რეაქცია აღწერილია თანმიმდევრობით, რომელიც წევრთა სასრული რაოდენობითაა, მაშინ ფილტრის განხორციელება შესაძლებელია როგორც სქემა ნაჩვენები ნახ. 4.3. აქ ასო აღნიშნავს სიგნალის დაგვიანების ელემენტებს გარკვეული დროით (თითო უჯრედზე); -ელემენტები, რომლებიც ამრავლებენ სიგნალს შესაბამის ფაქტორზე.
სქემა ნაჩვენებია ნახატზე. 4.3 არ არის ციფრული ფილტრის სქემა; ეს დიაგრამა წარმოადგენს ციფრული ფილტრაციის ალგორითმის გრაფიკულ გამოსახულებას და გვიჩვენებს სიგნალის დამუშავების დროს შესრულებული არითმეტიკული მოქმედებების თანმიმდევრობას.

ფიგურა: 4.3. არარეკურსიული ციფრული ფილტრის წრე
ციფრული ფილტრებისთვის, რომლებიც ამუშავებენ სიგნალებს აბსტრაქტული რიცხვითი მიმდევრობების სახით, ცნება „დროის შეფერხება“ მთლად სწორი არ არის. ამიტომ, ელემენტები, რომლებიც აყოვნებენ სიგნალს თითო უჯრედზე, ჩვეულებრივ აღინიშნება ციფრული ფილტრის სქემებზე, სიმბოლოთი, რომელიც აღნიშნავს ტრანსფორმაციის ენაზე სიგნალის დაგვიანებას. შემდეგში, ჩვენ ვიცავთ ამ აღნიშვნას.
დავუბრუნდეთ ციფრული ფილტრის სქემას, რომელიც ნაჩვენებია ნახაზზე. 4.3. ფილტრებს, რომლებიც იყენებენ მხოლოდ შეყვანის სიგნალის მნიშვნელობებს, ეწოდება მარტივი ან არა-რეკურსიული.
არარეკურსიული ფილტრის ალგორითმის წერა მარტივია, თუ ფილტრის იმპულსური რეაქცია ცნობილია. ალგორითმის პრაქტიკული განხორციელებისათვის აუცილებელია იმპულსური პასუხი შეიცავდეს ტერმინების სასრულ რაოდენობას. თუ იმპულსური პასუხი შეიცავს უსასრულო რაოდენობის ტერმინებს, მაგრამ ისინი სწრაფად იკლებს სიდიდეს, მაშინ ჩვენ შეგვიძლია შემოვიფარგლოთ ტერმინების სასრული რაოდენობით, უარი ვუთხრათ მათ, რომელთა მნიშვნელობები მცირეა. თუ იმპულსის რეაქციის ელემენტები არ შემცირდება სიდიდით, არარეკურსიული ფილტრის ალგორითმი აღმოჩნდება არარეალიზებული.

ფიგურა: 4.4. -ჯაჭვი
მაგალითად, განვიხილოთ უმარტივესი ციფრული ფილტრი, რომელიც მსგავსია -ჯაჭვას (ნახ. 4.4). -ჯაჭვის იმპულსურ პასუხს ფორმა აქვს
![]()
შესაბამისი ციფრული ფილტრის იმპულსური პასუხის დასაწერად, გამონათქვამი უნდა ჩანაცვლდეს, ამასთან, -ჯაჭვის იმპულსური პასუხი განზომილებიანია და ციფრული ფილტრის იმპულსური რეაგირება უნდა იყოს უგანზომილებიანი. ამიტომ, ჩვენ გამოვტოვებთ გამოხატვის ფაქტორს (4.2) და ციფრული ფილტრის იმპულსურ რეაგირებას ფორმაში ვწერთ
![]()
ასეთი იმპულსური პასუხი შეიცავს უსასრულოდ ბევრ ტერმინს, მაგრამ მათი ღირებულება ექსპონენციურად იკლებს და შეგიძლიათ შემოიფარგლოთ მხოლოდ ტერმინებით
ახლა თქვენ შეგიძლიათ დაწეროთ გამოხატვა სიგნალისთვის ფილტრის გამოსასვლელში
ეს გამოთქმა ასევე არის ციფრული ფილტრის ალგორითმი. ამ ფილტრის დიაგრამა ნაჩვენებია ნახატზე. 4.5.
ციფრული ფილტრების პროცესების ანალიზის მეორე მიდგომა მსგავსია ჩვეულებრივი ანალოგური სქემების ანალიზის ოპერატორის მეთოდისა, მხოლოდ ლაპლასის გარდაქმნის ნაცვლად გამოიყენება -ტრანსფორმა.

ფიგურა: 4.5. არა-რეკურსიული ციფრული ფილტრის დიაგრამა მსგავსია -ჯაჭვისა
მოდით განვსაზღვროთ ციფრული ფილტრის პარამეტრი, ელექტრული წრის გადაცემის ფუნქციის მსგავსი. ამისათვის გამოიყენეთ ციფრული ფილტრის იმპულსის რეაგირების -ვერსია:

ფუნქციას სისტემის ფილტრის ფუნქცია ეწოდება.
გამოხატვის (4.1) შესაბამისად, ციფრული ფილტრის გამოსასვლელი სიგნალი ტოლია შეყვანის სიგნალის დისკრეტული კონვოლუციისა და ფილტრის იმპულსური რეაქციისა. კონვოლუციის-ტრანსფორმაციის თეორემის გამოყენებაზე ამ გამონათქვამზე ვიღებთ იმას, რომ გამომავალი სიგნალის ტრანსფორმაცია ტოლია შეყვანის სიგნალის ტრანსფორმაციისა, გამრავლებული სისტემის ფილტრის ფუნქციაზე:
![]()
ამრიგად, სისტემის ფუნქცია ასრულებს ციფრული ფილტრის გადაცემის ფუნქციის როლს.
მაგალითად, მოდით ვიპოვოთ პირველი რიგის ციფრული ფილტრის სისტემის ფუნქცია, რომელიც მსგავსია -ჯაჭვისა:

ციფრული ფილტრების საშუალებით სიგნალების გადასვლის ანალიზის მესამე მეთოდი მსგავსია დიფერენციალური განტოლებების კლასიკური მეთოდისა. მოდით განვიხილოთ ეს მეთოდი წესრიგის ჯაჭვების მაგალითის გამოყენებით.
1-ლი რიგის უმარტივესი ანალოგური სქემა არის ჯაჭვი (იხ. სურათი 4.4), სიგნალების გავლა, რომლის მეშვეობითაც აღწერილია დიფერენციალური განტოლებით
![]()
დისკრეტული სქემისთვის, დიფერენციალური განტოლების (4.8) ნაცვლად, უნდა დაიწეროს განსხვავების განტოლება, სადაც შეყვანილი და გამომავალი სიგნალები მითითებულია დროის დისკრეტული მომენტებისთვის და წარმოებული პროდუქტის ნაცვლად უნდა გამოჩნდეს მიმდებარე სიგნალის მნიშვნელობების სხვაობა. 1 რიგის დისკრეტული ჯაჭვისთვის, განსხვავების განტოლება შეიძლება დაიწეროს საკმაოდ ზოგადი ფორმით
ჩვენ მივმართავთ განტოლებას - ტრანსფორმაციას
საიდანაც ვხვდებით სისტემის ფილტრის ფუნქციას
![]()
ფორმულა (4.10) საკმაოდ ზოგადი გამოხატულებაა 1-ლი რიგის ციფრული ფილტრის სისტემის ფუნქციისთვის. როდესაც, ეს ემთხვევა ადრე მიღებულ გამოთქმას (4.7) ციფრული ფილტრის სისტემის ფუნქციონირებისთვის, რომელიც ეკვივალენტურია -ჯაჭვისა.
მოდით ვიპოვოთ ციფრული ფილტრაციის ალგორითმი, რომელიც შეესაბამება სისტემის ფუნქციას (4.10). ამისათვის ჩვენ ამოხსნით განტოლებას (4.9) მიმართ
ამ ალგორითმის ეკვივალენტური წრე ნაჩვენებია ნახატზე. 4.6. არარეკურსიულ ფილტრთან შედარებით (იხ. ნახ. 4.5), აქ დამატებულია ერთგვარი "უკუკავშირი", რაც ნიშნავს, რომ გამომავალი სიგნალის მნიშვნელობები გამოიყენება შემდეგში

ფიგურა: 4.6. რეკურსიული ციფრული ფილტრის სქემა მსგავსია -ჯაჭვისა
გათვლები. ამ ტიპის ფილტრებს რეკურსიულს უწოდებენ.
ალგორითმი (4.11) შეესაბამება ფილტრს, რომელიც მთლიანად ექვივალენტურია ადრე განხილულ არაორკურსიულ ფილტრთან. მაგრამ გამოსასვლელი სიგნალის ერთი მნიშვნელობის დასადგენად არარეკურსიული ფილტრის ალგორითმის გამოყენებით (4.4), საჭიროა ოპერაციების შესრულება, ხოლო რეკურსიული ფილტრის ალგორითმის გამოყენებისას (4.11) მხოლოდ ორი ოპერაციაა საჭირო. ეს არის რეკურსიული ფილტრების მთავარი უპირატესობა. გარდა ამისა, რეკურსიული ფილტრები საშუალებას იძლევა სიგნალის დამუშავება უფრო მაღალი სიზუსტით, ვინაიდან ისინი იძლევა იმპულსური პასუხის უფრო სწორად განხორციელებას მისი "კუდის" გაუქმების გარეშე. რეკურსიული ფილტრები საშუალებას გაძლევთ დანერგოთ ალგორითმები, რომლებიც ზოგადად შეუძლებელია არაორკურსიული ფილტრების საშუალებით. მაგალითად, ფილტრით, რომელიც მუშაობს ნახაზის სქემის შესაბამისად. 4.6, არსებითად, იდეალური აკუმულატორ-ინტეგრატორია და აქვს ფორმის იმპულსური რეაქცია. ასეთი მახასიათებლის მქონე ფილტრის განხორციელება არ შეიძლება რეკურსიულ წრეში.
განხილული მაგალითებიდან ჩანს, რომ აზრი არა აქვს რეკურსიული ალგორითმების გამოყენებას გრძელი იმპულსური რეაგირების მქონე ციფრული ფილტრების შესაქმნელად. ამ შემთხვევებში უფრო აზრი აქვს რეკურსიული ფილტრების გამოყენებას.
არა-რეკურსიული ალგორითმების გამოყენების სფეროა ციფრული ფილტრების განხორციელება მცირე ტერმინების იმპულსის რეაგირებით. მაგალითად არის მარტივი დიფერენცირება, რომლის გამომავალი სიგნალი ტოლია შეყვანის სიგნალის ნამატის:
ასეთი ციფრული ფილტრის დიაგრამა ნაჩვენებია ნახატზე. 4.7.

ფიგურა: 4.7. უმარტივესი ციფრული დიფერენცირების სქემა
ახლა განვიხილოთ ზოგადი ციფრული ფილტრი, რომელიც აღწერილია განტოლებით
ეს განტოლება შეიძლება ჩაითვალოს როგორც ბრძანების სხვაობის განტოლება და როგორც ციფრული ფილტრაციის ალგორითმი, თუ მას სხვაგვარად გადავწერთ, კერძოდ

ფიგურა: 4.8. რეკურსიული ციფრული შეკვეთის ფილტრის სქემა
ალგორითმი (4.13) შეესაბამება სქემას, რომელიც ნაჩვენებია ნახაზზე. 4.8. მოდით იპოვოთ ასეთი ფილტრის სისტემის ფუნქცია. ამისათვის გამოიყენეთ განტოლება - ტრანსფორმაცია:
გამოხატვა (4.14) საშუალებას იძლევა დამყარდეს კავშირი ფილტრის წრის ელემენტების რხევებსა და სისტემის ფუნქციას შორის. კოეფიციენტები სისტემის ფუნქციის მრიცხველში განსაზღვრავს კოეფიციენტების მნიშვნელობებს at
(ფილტრის არარეკურსიულ ნაწილში), ხოლო მნიშვნელში კოეფიციენტები განსაზღვრავს ფილტრის რეკურსიულ ნაწილს.
48 ციფრული ფილტრი სასრული იმპულსის რეაგირებით. გამოსათვლელი ფილტრების გაანგარიშება.
სასრული იმპულსის რეაგირების ფილტრი (არარეკურსიული ფილტრი, FIR ფილტრი) ან FIR- ფილტრი (FIR აბრევიატურა საბოლოო იმპულსის პასუხად) - წრფივი ციფრული ფილტრების ერთ-ერთი ტიპი, რომლის დამახასიათებელი მახასიათებელია მისი იმპულსის რეაგირების დროით შეზღუდული (დროის გარკვეული მონაკვეთიდან იგი ხდება ზუსტად ნულოვანი). უკანა უკუკავშირის გამო ასეთ ფილტრს უწოდებენ არა-რეკურსიულსაც. ასეთი ფილტრის გადაცემის ფუნქციის მნიშვნელი არის გარკვეული მუდმივა.
სხვაობის განტოლება, რომელიც აღწერს ფილტრის შეყვანის და გამომავალ სიგნალებს შორის ურთიერთობას: სად პ- ფილტრის შეკვეთა, x(ნ) - შეყვანის სიგნალი, y(ნ) არის გამომავალი სიგნალი და ბ მე - ფილტრის კოეფიციენტები. სხვა სიტყვებით რომ ვთქვათ, გამომავალი სიგნალის ნებისმიერი ნიმუშის ღირებულება განისაზღვრება მასშტაბური მნიშვნელობების ჯამით პწინა ნიმუშები. სხვანაირად შეიძლება ითქვას: ფილტრის გამოსვლის მნიშვნელობა დროის ნებისმიერ მომენტში არის შეყვანის მყისიერი მნიშვნელობის საპასუხოდ და თანდათანობით დამსხვრეული რეაგირების ჯამი. პწინა სიგნალის ნიმუშები, რომლებიც კვლავ ახდენენ გავლენას გამომავალზე (შემდეგ პ-ანგარიშებით, იმპულსის გარდამავალი ფუნქცია ნულის ტოლი ხდება, როგორც უკვე აღვნიშნეთ, ამიტომ ყველა ტერმინი შემდეგ პასევე ნულის ტოლი ხდება). მოდით დავწეროთ წინა განტოლება უფრო ტევად ფორმაში:

ფილტრის ბირთვის საპოვნელად დააყენეთ
x(ნ) = δ( ნ)
სადაც δ ( ნ) არის დელტა ფუნქცია. შემდეგ FIR ფილტრის იმპულსური პასუხი შეიძლება დაიწეროს შემდეგნაირად:

იმპულსური პასუხის Z- გარდაქმნა გვაძლევს FIR ფილტრის გადაცემის ფუნქციას:

] Თვისებები
FIR ფილტრს აქვს მრავალი სასარგებლო თვისება, რაც ზოგჯერ უფრო სასურველია გამოიყენოს ვიდრე IIR ფილტრი. აქ არის რამოდენიმე მათგანი:
FIR ფილტრები ძლიერია.
FIR ფილტრები არ საჭიროებს უკუკავშირის განხორციელებას
FIR ფილტრების ფაზა შეიძლება გაკეთდეს ხაზოვანი
პირდაპირი ფორმის FIR ფილტრი
FIR ფილტრების განხორციელება შესაძლებელია სამი ელემენტის გამოყენებით: მულტიპლიკატორის, დამატებლისა და დაგვიანების ერთეულის გამოყენებით. ნახატზე ნაჩვენები ვარიანტია ტიპის 1 FIR ფილტრების პირდაპირი განხორციელება.

პირდაპირი ფორმის FIR ფილტრის განხორციელება
სამაგალითო პროგრამა
ქვემოთ მოცემულია FIR ფილტრის პროგრამის მაგალითი, დაწერილი C:
/ * FIR ფილტრი 128 ონკანისთვის * /
float fir_filter (float input)
სტატიკური ათწილადი ნიმუში;
acc \u003d 0,0 f; /* აკუმულატორი */
/ * გამრავლება და დაგროვება * /
ამისთვის (i \u003d 0; i< 128; i++) {
acc + \u003d (h [i] * ნიმუში [i]);
/ * გამომავალი * /
/ * დაგვიანებული სიგნალის კომპენსაცია * /
ამისთვის (i \u003d 127; i\u003e 0; i--)
ნიმუში [i] \u003d ნიმუში;
49 მონაცემთა გამარტივება. მოძრაობს საშუალოდ.
50 მონაცემთა გამარტივება. დამარბილება პარაბოლებით.
51 მონაცემთა გამარტივება. სპენსერის გამარტივება.
52 მონაცემთა გამარტივება. საშუალო ფილტრაცია.
საშუალო მოძრაობა, კურდღლების დამარბილება, სპენსერის დამარბილება, საშუალო ფილტრაცია
ფიზიკური პროცესების პარამეტრების დროულად ნელა შეცვლის მეთოდების შემუშავებისას მნიშვნელოვანი ამოცანაა აღმოფხვრას ხმაურის ზემოქმედება ან შემთხვევითი ჩარევა, რომლებიც ზედმეტი ზემოქმედება ხდება დამუშავებულ სიგნალზე პირველადი გადამყვანიდან.
ამ ეფექტის აღმოსაფხვრელად შეგიძლიათ გამოიყენოთ მონაცემთა დაგლუვება. ამის ერთ-ერთი მარტივი გზაა საშუალო არითმეტიკა. როდესაც გამოიყენება, დისკრეტული ფუნქციის თითოეული მნიშვნელობა (დამუშავებული მონაცემთა მასივი) გამოითვლება გამოხატვის შესაბამისად:
სად არის საშუალო არითმეტიკული წერტილების რაოდენობა (კენტი მთელი რიცხვი);
ფუნქციის მნიშვნელობა გადაცემამდე დამუშავებამდე;
არსებობს დამარბილების სხვა, საკმაოდ ეფექტური მეთოდები, მაგალითად, მეორე ხარისხის პარაბოლა ხუთი, შვიდი, ცხრა და თერთმეტი წერტილის მიხედვით, გამონათქვამების შესაბამისად:
ან მეოთხე ხარისხის პარაბოლა შვიდი, ცხრა, თერთმეტი და ცამეტი წერტილით:
პრაქტიკულ გამოყენებებში სხვა ეფექტური მეთოდები კარგ შედეგს იძლევა, მაგალითად, 15 პუნქტიანი სპენსერის დამარბილება:
შეცვალეთ რთული გამონათქვამი ამ გამონათქვამებში, სადაც შეგიძლიათ განსაზღვროთ შესაბამისი ტრანსფორმაციის გადაცემის ფუნქცია.
საშუალო არითმეტიკისთვის
ფრჩხილებში გამოხატვა არის გეომეტრიული პროგრესია მნიშვნელობით, ამიტომ ეს გამოხატვა შეიძლება წარმოდგენილ იქნას როგორც:
 .
.
ეს ფორმულა წარმოადგენს დაბალი გამავლობის ფილტრის გადაცემის მახასიათებელს და აქედან ჩანს, რომ რაც უფრო მეტი ტერმინებია ჩართული საშუალოზე, მით მეტია მაღალი სიხშირის ხმაურის კომპონენტების ჩახშობა სიგნალში (იხ. სურათი 6.1).
ამასთან, დროის ტენდენციების დამუშავებისას სიხშირის კონცეფცია განსხვავდება სიგნალების დამუშავების ანალოგიური კონცეფციისგან. ეს გამოწვეულია იმით, რომ დროის ტენდენციების შესწავლისას არა მათი სიხშირის კომპოზიციაა საინტერესო, არამედ ცვლილების სახეობა (ზრდა, კლება, მდგრადობა, ციკლურობა და ა.შ.)
ეგრეთ წოდებული ევრისტიკური ალგორითმების გამოყენება ასევე ეფექტურია მონაცემთა გასწორებისთვის.
ერთ-ერთი მათგანია მედიანური ფილტრაცია. განზომილების მოცურების დროის ფანჯარაში მისი განხორციელებისას, როდესაც მთელი რიცხვი არის უცნაური რიცხვი, ცენტრალურ ელემენტს ანაცვლებს მიმდევრობის შუა ელემენტი, რომლებიც ალაგებულია მნიშვნელობებით ზრდადი თანმიმდევრობით, გაბრტყელებული სიგნალის მონაცემთა მასივის ელემენტებით, რომლებიც მოხვდება დროის ფანჯარაში. საშუალო ფილტრაციის უპირატესობა არის იმპულსური ხმაურის ამოღების შესაძლებლობა, რომლის ხანგრძლივობა არ აღემატება, პრაქტიკულად შეუფერხებლად შეცვლილი სიგნალების დამახინჯების გარეშე. ხმაურის ჩახშობის ამ მეთოდს არ გააჩნია მკაცრი მათემატიკური დასაბუთება, მაგრამ გამოთვლების სიმარტივემ და მიღებული შედეგების ეფექტურობამ განაპირობა მისი ფართო გამოყენება.

სურათი 6.1 - გადაცემის მახასიათებლების დიაგრამა
საშუალო არითმეტიკული მოქმედებები m \u003d 5, 7, 9, 11-ისთვის
კიდევ ერთი საინტერესო დაგლუვების ალგორითმი არის საშუალო საშუალო. მისი არსი შემდეგია. მოცურების დროის ფანჯარაში, ზომები (- უცნაური მთელი რიცხვი), მონაცემთა მასივის ელემენტები ალაგდება ზრდადი თანმიმდევრობით, შემდეგ კი პირველი და ბოლო ელემენტები ამოღებულია შეკვეთილი თანმიმდევრობიდან (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
ეს მეთოდი საშუალებას გაძლევთ აღკვეთოთ იმპულსური და რადიოსიხშირული ჩარევა, ასევე მიაღწიოთ სიგნალის კარგ გამარტივებას.
| " |