Mindez azzal kezdődött, hogy a barátom barátja barátja segítséget nyújtott ezekkel a fettekkel. Jedi pletykái eljutottak előttem, feliratkoztam a megjegyzésekben a linkre. Segíteni. Nos, remélem.
Ez a történet a harmadik, vagy a kurzus emlékeiről mentél bennem, amikor én magam átadtam a TSO-knek, és megerőszakoltam egy cikket az érdeklődők számára, hogy a digitális szűrők hogyan dolgoznak, de akik természetesen megijednek a hegyes képletek és a pszichedelia Képek (már nem beszélek tankönyvekről).
Általánosságban elmondható, hogy tapasztalataimban a tankönyvek helyzetét a jól ismert kifejezés írja le arról, hogy a fák nem láthatók az erdőben. Aztán azt mondjuk, hogy mikor fogsz megijeszteni a Z-konverziót és a formulákat a polinomok felosztásával, amelyek gyakran hosszabbak, mint két táblán, és a téma érdeklődése rendkívül gyorsan elfogy. Egyszerűen kezdjük, hogy megértsük, hogy megértsük, mi történik, teljesen opcionális, hogy hosszú komplex kifejezéseket festjen.
Tehát egy kezdetre néhány egyszerű alapfogalom.
1. Impulzus jellemző.
Tettem, van egy doboz négy következtetéssel. Nem vagyunk olyan koncepció, amelyen belül van, de pontosan tudjuk, hogy két bal oldali kimenet a bejárat, és a két jobb a kijárat. Próbáljunk nagyon rövid impulzust alkalmazni egy nagyon nagy amplitúdóra, és nézd meg, mi lesz a kijáratnál. Nos, miért, olyan, mint ebben a quadrupolimakerben, nem világos, mert nem világos, hogy leírja, és így legalább látni fog.
Itt kell mondani, hogy a rövid (általában a beszéd végtelenül rövid) az impulzus nagy (általában beszéd, végtelen) amplitúdó az elméletben Delta funkciónak nevezik. By the way, a vicces dolog az, hogy az integrál erről végtelen A funkciók egyenlőek. Ilyen normalizáció.
Szóval, amit láttunk egy quadrupolimaker kijáratánál, egy delta funkciót küldött, hívott impulzus jellemző Ez a négyágyat. Bár azonban nem világos, hogy mit segít nekünk, de emlékezzünk arra, hogy a kapott eredményt, és továbblépjünk a következő érdekes koncepcióra.
2. Vágás.
Ha röviden beszélünk, akkor a konvolúció egy matematikai művelet, amely csökkenti a funkciók termékének integrálását:
![]()
Ez látható, ahogy látható, csillag. Azt is látjuk, hogy amikor egy konvolúció, az egyik funkció a "közvetlen" sorrendben történik, és a "visszafelé" haladunk. Természetesen az emberiség értékesebbé tétele, egy konvolúció diszkrét esete, mint bármely integrál, összefoglalás:

Úgy tűnik, hogy néhány szomorú matematikai absztrakció. Valójában azonban a konvolúció talán a világ legcsodálatosabb jelensége, meglepően rosszabb, mint egy személy megjelenése a fényért, az egyetlen különbség, hogy a gyermekek a legtöbb emberből származnak a legtöbb szélsőséges esetekben évekig Míg arról, hogy mi a konvolúció, és milyen hasznos és csodálatos, a föld népességének hatalmas része nem ismeri fel az életüket.
Tehát ennek a műveletnek a hatalma, hogy ha F bármilyen tetszőleges bemeneti jel, és g a négyfajta impulzus jellemzője, e két funkció konvolúciójának eredménye hasonló lesz ahhoz, amit kapnánk, áthaladunk az F-ben ez a négypólusú.
Ez az, hogy az impulzus jellemző a növekvő hatás tekintetében egy négyágyas tulajdonság teljes tulajdonsága, és a bemeneti jel bitjei lehetővé teszik, hogy visszaállítsa a kimeneti jelet, amely megfelel. Ami engem illet, csak félelmetes!
3. Szűrők.
Egy impulzus jellemző és egy konvolúcióval sok érdekes dolgot hozhat létre. Például, ha a jel hangos, akkor a reverb, az echo, a kórus, a flanger és a sokat szervezheti egymást; Megkülönböztetheti és integrálhatja ... Általában létrehozhat semmit. Számunkra most a legfontosabb dolog az, hogy természetesen a szűrőket is könnyen beszerzi a konvolúcióval.
Valójában egy digitális szűrő, és egy bemeneti jel fúró, amely a kívánt szűrőnek megfelelő impulzus jellemzővel rendelkezik.
Természetesen az impulzus jellemzőnek valahogyan kell lennie. Természetesen már rájöttünk, hogy mikor mérjük meg, de ilyen feladatban egy kicsit egy kicsit - ha már összegyűjtöttük a szűrőt, miért mérik még valamit, használhatod, ahogy ez. Igen, és emellett a digitális szűrők legfontosabb értéke, hogy azok a tulajdonságokkal rendelkeznek (vagy nagyon nehéz elérhetők) a valóságban - például egy lineáris fázisban. Tehát semmilyen módon nem lehet mosni, csak számolni kell.
4. Pulzus-jellemző megszerzése.
Ezen a helyen a legtöbb publikáció a témában, a szerzők elkezdenek önteni a Z-transzformációk és a polinomok frakcióinak olvasójába, és végül zavarja. Nem fogom ezt megtenni, csak röviden magyarázd el, miért és miért a gyakorlatban a progresszív nyilvánosság számára nem sok szükséges.
Tegyük fel, hogy eldöntöttük, mit szeretnénk a szűrőn, és egy egyenletet készített, amely leírja. Továbbá, annak érdekében, hogy egy impulzus jellemzőt találjon, helyettesítheti a delta funkciót a származtatott egyenlethez, és megkaphatja a kívánt értéket. Az egyetlen probléma az, hogyan kell csinálni, az időben delta-funkcióért ról rőla régiót egy ravasz rendszer adja, és általában minden végtelen. Tehát ebben a szakaszban minden olyan félelmetes lesz.
Itt történik, és ne feledje, hogy van olyan dolog, mint a Laplace transzformáció. Önmagában ez nem egy font ömlött. Az egyetlen ok, amiért rádiómérnöki szenved, az a tény, hogy az érvelés terén az átmenet, amelyre ez az átalakulás, néhány dolog valóban könnyebbé válik. Különösen ugyanaz a delta funkció nagyon könnyen kifejezhető, ami annyi bajt szolgáltatott az időtartományban - csak egy egység!
Z-konverzió (aka laurent transzformáció) - Laplace konverziós változat diszkrét rendszerekhez.
Vagyis a Laplace transzformáció (vagy a Z-konverzió szükség esetén) alkalmazása a kívánt szűrőt leíró függvényhez, a beérkezett egységbe helyettesítve, és visszaállunk, egy impulzus jellemzőt kapunk. A hangok könnyen szeretnék próbálni. Nem fogok kockáztatni, mert amint azt már említettük, a Laplace átalakulása kemény dolog, különösen az ellenkezője. Hagyjuk a szélsőséges esetre, és egyszerűbb módokat keresünk a kívánt módon. Számos közülük vannak.
Először is, emlékszel egy másik csodálatos természetre - az amplitúdó-frekvencia és impulzus jellemzői összekapcsolódnak egy jó és ismerős Fourier transzformációval. Ez azt jelenti, hogy bármilyen választ adhatunk az ízlésedre, a Fourier fordított átalakulását (legalább folyamatos, akár diszkrét), és megkapja a rendszer impulzus jellemzőit, hogy végrehajtja. Ez csak csodálatos!
Itt azonban nem lesz probléma. Először is, az impulzus jellemző, amit kapunk, a legvalószínűbb lesz végtelenül (nem fogok magyarázni, miért; a világ annyira elrendezve van), ezért egy bizonyos ponton meg kell vágnunk (a nulla-os értéket). De ez nem lesz egyszerűen ennek eredményeként, amint azt várni kell, a kiszámított szűrő ACHM torzítása lesz - hullámos lesz, és a frekvenciavágás meghal.
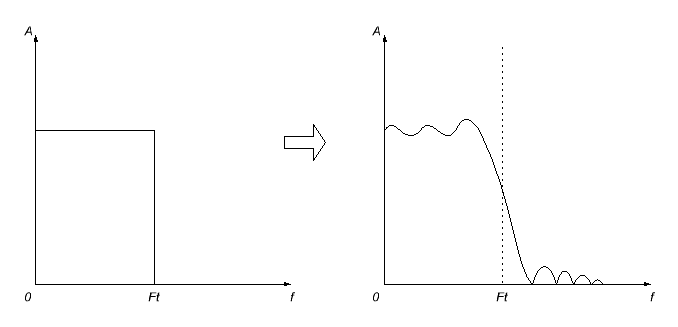
A hatások minimalizálása érdekében különböző simító ablakfunkciók vonatkoznak egy rövidített impulzus jellemzőre. Ennek eredményeképpen a válasz általában még inkább elmosódott, de eltűnik a kellemetlen (különösen a sávszélességben) oszcillációban. 
Valójában, az ilyen kezelés után egy dolgozó impulzus jellemzőt kapunk, és képes egy digitális szűrőt létrehozni.
A második számítási módszer még könnyebb - a legnépszerűbb szűrők impulzus jellemzői régóta kifejezve az analitikai formában. Csak az értékek helyettesítésére szolgál, és az ablakfunkció eredményére vonatkozik. Tehát nem is tudsz semmilyen transzformációt is figyelembe venni.
Természetesen, ha a cél az, hogy az egyes rendszer viselkedését emulálja, lehetséges, hogy az impulzus jellemzője a szimulátorban:

Itt voltam a bemeneti RC-lánc impulzushoz 100 500 V-os feszültséggel (igen, 100,5 kV), amelynek időtartama 1 μs, és megkapta az impulzus jellemzőjét. Nyilvánvaló, hogy ez nem történik a valóságban, hanem a szimulátorban ez a módszer, amint azt látod, nagyszerűen dolgozik.
5. Megjegyzések.
A fenti fellebbezés az impulzus jellemző rövidítéséről természetesen az úgynevezett. Szűrők véges impulzus jellemzővel (FIR / KI szűrők). Vannak egy csomó értékes tulajdonságuk, beleértve a lineáris fázist (bizonyos feltételek mellett egy impulzus jellemző előállításához), amely a szűrés, valamint az abszolút stabilitás, valamint az abszolút stabilitás hiányát biztosítja. Vannak szűrők végtelen impulzus jellemzővel (IR / BIH szűrők). Ezek kevésbé erőforrás-intenzívek a számítások értelmében, de már nem szerepelt az előnyök.
A következő cikkben remélem, hogy szétszereljük a digitális szűrő gyakorlati megvalósításának egyszerű példáját.
10. előadási szám.
"Digitális szűrők véges impulzus jellemzővel"
A fizikailag megvalósított digitális szűrő átviteli funkciója véges impulzus jellemzővel (KIH szűrő) ábrázolható
(10.1).
A kifejezés (10.1) cseréje esetén a QIH szűrő frekvenciaválaszát kapjuk
![]() (10.2),
(10.2),
hol ![]() - amplitúdó-frekvencia jellemző (ACH) szűrő
- amplitúdó-frekvencia jellemző (ACH) szűrő
![]() - fázisfrekvencia-jellemző (FCH) szűrő.
- fázisfrekvencia-jellemző (FCH) szűrő.
Fázis késleltetés a szűrő definiálása
![]() (10.3).
(10.3).
Csoportos késleltetés a szűrő definiálása
![]() (10.4).
(10.4).
A QC szűrők megkülönböztető jellemzője az állandó fázis és csoport késedelmek végrehajtásának lehetősége, azaz Lineáris fch
(10.5),
hol egy. - Állandó. Ha ez a feltétel teljesül, a szűrőn áthaladó jel nem torzítja az űrlapot.
A lineáris FCH-t tartalmazó feltételek megjelenítéséhez írja le a QC szűrő frekvenciaválaszát, figyelembe véve (10.5)
![]() (10.6).
(10.6).
Az egyenlőség érvényes és képzeletbeli részei egyenlő
 (10.7).
(10.7).
A második egyenlet megosztása az elsőre, kapunk
 (10.8).
(10.8).
Végül le tudsz írni
 (10.9).
(10.9).
Ez az egyenletnek két megoldása van. Előszöra. \u003d 0 megfelel az egyenletnek
 (10.10).
(10.10).
Ez az egyenlet egy olyan megoldással rendelkezik, amely megfelel az önkényesnekh (0) (sin (0) \u003d 0) és h (n) \u003d 0 n \u003e 0. Ez a megoldás megfelel a szűrőnek, amelynek impulzus jellemzője, amelynek egyetlen nonzero számlálása az idő kezdeti pillanatában. Az ilyen szűrő gyakorlati érdeklődést jelent.
Egy másik döntés megtalálja. Ugyanakkor, keresztirányban több számláló és denominátorok (10.8)
(10.11).
Innen van
![]() (10.12).
(10.12).
Mivel ez az egyenlet tekintete egy Fourier sorozat, annak megoldása, ha létezik, az egyetlen.
Könnyű látni, hogy az egyenlet megoldása meg kell felelnie a feltételeknek
(10.13),
(10.14).
Az állapotból (10.13) következik, hogy a szűrő minden sorrendjébenN. Csak egy fázis késleltetés vana. Amelyen az FFH szigorú linearitása érhető el. Az állapotból (10.14) következik, hogy a szűrő impulzus jellemzőinek szimmetrikusnak kell lennie a páratlan ponthoz képestN. , és az intervallum középpontjához képest (10.1. Ábra).
 |
Egy ilyen szűrő frekvenciaváltsága (páratlanN. ) írható
(10.15).
Csere a második összegbenm \u003d n -1- n, kap
(10.16).
Óta h (n) \u003d h (n -1- n) ), akkor két összeg kombinálható
 (10.17).
(10.17).
Helyettesítő, kapunk
(10.18).
Ha jelöli
 (10.19),
(10.19),
akkor végül rögzíthetsz
 (10.20).
(10.20).
Így egy lineáris fch szűrőnk van
 (10.21).
(10.21).
Az isN. Hasonlóképpen, mi lesz
 (10.22).
(10.22).
Cserélje ki a második összeget, kapunk
 (10.23).
(10.23).
Csere, kap
(10.24).
Jelzett
![]() (10.25),
(10.25),
végül leszünk
 (10.26).
(10.26).
Így egy QIH szűrő lineáris fch és egyenletes sorrendbenN rögzíthető
 (10.27).
(10.27).
A jövőben az egyszerűségért csak furcsa rendeléssel rendelkező szűrőket tekintünk.
A szűrő átviteli funkciójának szintézisében a kezdeti paraméterek általában a frekvenciaváltság követelményei. A KIH szűrők szintézisének sok technikája van. Tekintsük néhányat.
Mivel bármilyen digitális szűrő frekvenciaváltsága periodikus frekvencia funkció, akkor a Fourier soraként ábrázolható
![]() (10.28),
(10.28),
ahol a Fourier sorozat együtthatók egyenlőek
 (10.29).
(10.29).
Látható, hogy a Fourier sorozat együtthatókh (N. ) Egybeesik a szűrőimpulzus jellemzőinek együtthatókkal. Ezért, ha egy analitikai leírást a kívánt frekvencia válaszát a szűrő ismert, akkor könnyen meghatározhatja az együtthatóit az impulzus jellemző, és rájuk - az átviteli függvény a szűrő. A gyakorlatban azonban ez nem valósul meg, mivel az ilyen szűrő impulzus jellemzője végtelen hosszúságú. Ezenkívül egy ilyen szűrőt fizikailag impulzus jellemzőnek kell végrehajtani -¥ És a végső késedelem nem fogja végrehajtani ezt a szűrőt fizikailag megvalósítani.
A KIH-szűrő megszerzésének egyik lehetséges módszere, a megadott frekvenciaváltság közelítése a Fourier végtelen sorának és a szűrő impulzus jellemzőjének csonkítása, hiszih (n) \u003d 0-at. Azután
 (10.30).
(10.30).
Az átviteli funkció fizikai megvalósíthatóságaH (Z. ) érhető el sokszorosítássalH (z) be.
 (10.31),
(10.31),
hol
(10.32).
Az átviteli funkció ilyen módosításával a szűrő amplitúdója nem változik, és a csoport késlelteti a folyamatos értéket.
Például kiszámítjuk az alacsony frekvenciájú kiszűrőt a frekvenciaváltással
 (10.33).
(10.33).
A (10.29) szerint a szűrőimpulzus jellemzőinek együtthatóit a kifejezés írja le
 (10.34).
(10.34).
Most (10.31) érhető el egy kifejezést a hajtómű funkcióhoz
 (10.35),
(10.35),
hol
(10.36).
A számított szűrő amplitúdó jellemzői különbözőekN. A 10.2. Ábrán bemutatott.

10.2
A pulzálás sávszélességben és késleltetési sávokban fordul elő a Fourier sorozat lassú konvergenciája miatt, amely viszont a sávszélesség frekvenciáján lévő függvény jelenlétének köszönhető. Ezek a hullámok ismertek pulzáló gibbs.
A 10.2. Ábra azt mutatja, hogy növekszikN. A pulzációs frekvencia növekszik, és az amplitúdó mind az alsó, mind a felső frekvenciákon csökken. Az utolsó pulzálás amplitúdója azonban a sávszélességben és az első ripple a késedelem stroke szinte változatlan marad. A gyakorlatban az ilyen hatások gyakran nemkívánatosak, ami megköveteli a Gibbs hullámok csökkentésének módját.
Csonkított impulzus jellemzőh (N. ) a szükséges végtelen impulzus jellemző és néhány termék terméke ablakfunkciók w (n) n hosszúságú (10. ábra).
![]() (10.37).
(10.37).
 |
A Fourier sorozat egyszerű csonkításának szempontjából négyszögletes ablak
 (10.38).
(10.38).
Ebben az esetben a szűrő frekvenciaváltsága komplex konvolúcióként jeleníthető meg
 (10.39).
(10.39).
Ez azt jelenti, hogy a kívánt jellemző "homályos" változata lesz.
A feladat csökken, hogy megtalálja az ablakok funkcióit, hogy csökkentse a Gibbs impulzusokat ugyanazzal a szűrőszelektivitással. Ehhez először meg kell vizsgálni az ablakfunkció tulajdonságait a téglalap alakú ablak példáján.
A téglalap alakú ablakfunkció spektruma írható
 (10.40).
(10.40).
A téglalap alakú ablak funkciójának spektrumát a 10.4. Ábrán mutatjuk be.

10.4.
Mivel a fő szirompektrum szélessége egyenlő.
Az oldalsó szirmok jelenléte az ablakfüggvény spektrumában a Gibbs impulzusok növekedéséhez vezet a frekvencia-válaszban. Ahhoz, hogy a kis pulzálás a sávszélesség és a nagy csillapítás zenekar a lökete a késés, az szükséges, hogy a területen korlátozza oldalán szirmok tesz egy kis részét a területen korlátozza a fő szirom.
A fő szirom szélessége határozza meg a kapott szűrő átmeneti zónájának szélességét. A szűrő nagy szelektivitásához a főszirom szélessége a lehető legkisebbnek kell lennie. Amint az előbbiből látható, a fő szirom szélessége csökken a szűrő sorrendjének növelésével.
Így a megfelelő Windows funkciók tulajdonságai a következőképpen alakíthatók ki:
- az ablak funkciót időben kell korlátozni;
- az ablakfunkció spektrumának leginkább a frekvencia által korlátozott függvényt kell megközelítenie, azaz minimális energiája van a fő sziromon kívül;
- az ablakfunkció fő szirompektrumának szélessége kicsi.
A leggyakrabban használja a következő Windows funkcióit:
1. Téglalap alakú ablak. Fent megfontolták.
2. Hamming ablak (Hamming).
 (10.41),
(10.41),
hol.
Ezzel az ablakkal Hanna ablak (hanning).
3. Blackman ablak (Blackman).
 (10.42).
(10.42).
4. Bartlett ablak (Bartlett).
 (10.43).
(10.43).
A megadott ablakfunkciók használatával beépített szűrőjelzők a 10.1 táblázatra csökkentek.
|
Ablak |
A fő szirom szélessége |
Pulzációs együttható,% |
||
N \u003d 11. |
N \u003d 21. |
N \u003d 31. |
||
|
Négyszögletes |
22.34 |
21.89 |
21.80 |
|
|
Hangolás |
2.62 |
2.67 |
2.67 |
|
|
Kalapács |
1.47 |
0.93 |
0.82 |
|
|
Fekete ember |
0.08 |
0.12 |
0.12 |
|
A pulzálás együtthatót úgy definiáljuk, mint az arány a maximális amplitúdója az oldalsó szirom, hogy az amplitúdó a fő szirom spektrumában az ablak funkciót.
A szűrő szükséges sorrendjének és a legmegfelelőbb ablakfunkció kiválasztásához a valódi szűrők kiszámításakor használhatja a 10.2.
|
Átmeneti |
Egyenetlenség Áthaladó (db) |
Csillapítás B. brokes (db) |
|
|
Négyszögletes |
|||
|
Hangolás |
|||
|
Kalapács |
|||
|
Fekete ember |
Amint az a 10.1. Táblázatból látható, van egy bizonyos kapcsolat a ferde-együttható és a fő szirom szélessége között az ablakfunkció spektrumában. Minél kisebb a hullámos együttható, annál nagyobb a főszirom szélessége, ezért az átmeneti zóna a frekvencia-válaszban. Az alacsony hullámok biztosítása a sávszélességben, ki kell választania egy megfelelő hullámos együtthatóval rendelkező ablakot, és biztosítja az átmeneti zóna szükséges szélességét, hogy megnövelje a szűrőt N.
Ez a probléma megoldható a Kaiser által kínált ablak segítségével. A KAISER ablak funkciónak van nézete
 (10.44),
(10.44),
ahol A független paraméter, ![]() , I 0 - Bessel funkció az elsőfajta nulla sorrendben
, I 0 - Bessel funkció az elsőfajta nulla sorrendben
 (10.45).
(10.45).
A KAISER ablak vonzó tulajdonsága a kis értékekből a nagy értékekből származó ripple együttható zökkenőmentes változásai, amikor csak egy paramétert változtatnak. Ebben az esetben, mint más Windows funkciók esetében, a fő szirom szélessége a szűrő sorrendjével állítható be.
A valódi szűrő fejlesztésében meghatározott fő paraméterek:
Sávszélesség - w p;
Törött sáv - w a;
Maximális megengedhető pulzálás a sávszélességben - A P;
Minimális csillapítás a késedelem löketében - A;
-mintavételi frekvencia -s.
Ezeket a paramétereket a 10.5. Ábrán szemléltetjük. Ugyanakkor a sávszélesség maximális ripple meghatározása
![]() (10.46),
(10.46),
és minimális csillapítás a késedelem stroke-ban
A szűrő kiszámításának viszonylag egyszerű eljárása a Kaizer ablakkal a következő lépéseket tartalmazza:
1. A H (n) szűrő impulzus jellemzőit meghatározzuk, feltéve, hogy a frekvencia-válasz ideális
 (10.48),
(10.48),
ahol (10.49).
2. A D paraméter van kiválasztva
![]() (10.50),
(10.50),
hol  (10.51).
(10.51).
3. Az A és A P valódi érték jelenleg érvényes a képletek (10.46), (10.47) szerint.
4. A. paraméter
 (10.52).
(10.52).
5. D. paraméter
 (10.53).
(10.53).
6. A szűrő sorrendjének legkisebb furcsa értéke az állapotból
![]() (10.54),
(10.54),
 (10.57)
(10.57)
ezt követi
Mivel a szűrő jellemző minták az átviteli funkciójának együtthatók, akkor az állapot (10.59) azt jelenti, hogy az összes szűrő együttható kódja csak egy frakcionált rész és egy jelkibocsátás, és nem tartalmaz egy teljes részt.
A kisülések száma a tört része a szűrő együtthatók határozzuk meg a feltétel kielégítéséhez az átviteli függvény a szűrő kvantált együtthatók által meghatározott követelményeket a közelítés a referencia áttétel a pontos értékek az együtthatók.
A szűrő bemeneti jelek mintáinak abszolút értékeit általában normalizálják, így
Ha az elemzés elvégzésére irányuló Qih szűrő lineáris FCH az algoritmus kiszámításához a kimeneti jel lehet a következő.
hol - a szűrő S K koefficienseire kerekítve.
Ez az algoritmus megfelel a szűrő blokkdiagramjának, a 10.5. Ábrán látható.
 |
Ennek az algoritmusnak két módja van. Az első esetben az összes szorzási művelet pontosan történik, és a munkák kerekítése hiányzik. Ebben az esetben a munkák mérete S + S K, ahol S in a bemeneti jel kiürítése, és az S K a szűrő együtthatók kisülése. Ebben az esetben a 10.5. Ábrán látható szűrő blokkdiagramja pontosan megfelel az igazi szűrőnek.
Az algoritmus (10.61) végrehajtásának második módjában a szorzási művelet mindegyik eredménye lekerekítés, azaz A munkákat valamilyen hiba alapján számítják ki. Ebben az esetben meg kell változtatni az algoritmust (10.61), hogy figyelembe vegye a hibát, kerekítési munkákat
Ha a visszaszámlálás értékeket a szűrő kimeneti jel számítjuk ki az első módszer (pontos értékei munkák), majd a diszperziót a kimeneti zaj definiáljuk
![]() (10.66),
(10.66),
azok. Attól függ, hogy a bemeneti jel és a szűrő együtthatók értékeinek megszüntetésétől függ. Innen megtalálhatja a szükséges számú bemeneti kibocsátásokat
 (10.67).
(10.67).
Az S IN és S K ismert értékei szerint meghatározhatja a kimeneti kód frakciójához szükséges kisülések számát
Ha az értékek a kimenő jel számít szerint számítjuk a második módszer, ha minden egyes termék van kerekítve, hogy az SD kisülések, a diszperzió a zaj a kerekítés által létrehozott minden egyes szorzók fejezhető a mentesítési a munka mint
DR és jel-zaj arány az SNR kimenet kimenetén. A decibelek bemeneti jelének dinamikus tartományának értékét úgy határozzák meg, hogy
![]() (10.74),
(10.74),
ha egy max és egy perc a szűrő bemeneti jel maximális és minimális amplitúdója.
A szűrő, a decibelben expresszált szűrőjelben lévő jel-zaj arány meghatározása
![]() (10.75),
(10.75),
meghatározza a kimeneti sinusoidal jelszűrő jel átlagos négyzetértékét, amplitúdóval, és
(10.77)
meghatározza a szűrő kimenetének zajelhitelét. (10,75) és (10,76) egy max \u003d 1-en kapunk expressziót a szűrő kimeneti zajának diszperziójához
![]() (10.78).
(10.78).
Ez a szűrő kimeneti zaj diszperziójának értéke használható a bemeneti és kimeneti szűrőjelek kiáramlásának kiszámításához.
Fontolja meg a legegyszerűbb digitális szűrőket - állandó paraméterekkel rendelkező szűrők.
A bemeneti jelet a digitális szűrő bemenetbe táplálják az intervallumot követő numerikus értékek szekvenciájaként (4.1. Ábra, A). Ha a digitális szűrő összes következő jelértékét kiszámítják, a számítási algoritmus kimeneti jelének következő értéke lehet a legkülönbözőbb; A számítási folyamatban az utolsó bemeneti jel mellett a bemeneti jel használható.
a bemeneti és kimeneti jelek korábbi értékei: A digitális szűrő kimenetén lévő jel szintén az intervallumot követő numerikus értékek szekvenciáját is jelenti. Ez az intervallum az egész digitális jelfeldolgozó eszköz számára.

Ábra. 4.1. Bemeneti jel és a digitális szűrő kimeneten
Ezért, ha a legegyszerűbb jelet egy egységimpulzus formájában adja meg a digitális szűrő bemenethez (4.2. Ábra, A)
![]()
ezután a kimeneten egy jelet kapunk a numerikus értékek diszkrét sorrendjének formájában
A hagyományos analóg áramkörökkel analógiával, ezt a válaszjelt egy impulzusszűrővel jellemeztük (4.2. Ábra, b). Az analóg áramkör impulzusjellemzőivel ellentétben a funkció dimenziómentes.

Ábra. 4.2. A digitális szűrő egyetlen impulzus és impulzus jellemzői
Adjunk tetszőleges diszkrét jelet a szűrő bemenetre. 4.1, a), amely diszkrét értékek
A szűrő kimenetének első elemének hatása alatt egy szekvenciával megszorozva szekvenciát szorozunk, és nagyságrendben, stb.

Így a kimeneti jel diszkrét bemeneti jel és impulzus jellemző. Ebben a tekintetben a digitális szűrők hasonlóak a hagyományos áramkörökhöz, ahol a kimeneti jel megegyezik a bemeneti jelekkel és az impulzus jellemzővel.
A (4.1) képlet digitális szűrő algoritmus. Ha a szűrőimpulzus jellemzőt egy véges számú tagú szekvencia írja le, akkor a szűrő az 1. ábrán bemutatott sémaként valósítható meg. 4.3. Itt a levél jelzi a jel késleltetésének elemeit az idő alatt (cellánként); - olyan elemek, amelyek a jelet a megfelelő arányhoz szorozzák.
Az 1. ábrán bemutatott ábra. 4.3, nem egy digitális szűrő elektromos diagramja; Ez a rendszer egy digitális szűrő algoritmus grafikus képe, és a jelfeldolgozás során elvégzett aritmetikai műveletek sorozata látható.

Ábra. 4.3. Digitális digitális szűrési séma
A digitális szűrők esetében az absztrakt numerikus szekvenciák formájában történő feldolgozási jelek, a "késleltetés" fogalma nem teljesen helyes. Ezért, elemek, hogy késlelteti a jelet per sejt digitális szűrő diagramok általában megjegyezte jelölő szimbólum jel késleltetési a konverziót. A jövőben betartjuk ezt a megnevezést.
Visszatérjünk az 1. ábrán bemutatott digitális szűrő diagramjához. 4.3, Ilyen szűrők, ahol csak a bemeneti értékeket használják kiszámítására, egyszerű vagy nem neurisztikusnak nevezik.
A nem ejektorszűrő algoritmusa könnyen rögzíthető, ha az impulzusszűrő impulzus jellemzője ismert. Az algoritmus gyakorlati megvalósításához szükséges, hogy az impulzus jellemzője véges számú tagot tartalmazza. Ha az impulzus jellemzője végtelen számú tagot tartalmaz, de gyorsan csökken a nagyságrendben, akkor csak a véges számú tagokra korlátozódik, amelyek kicsiek. Ha az impulzus jellemző elemei nem csökkennek nagyságrendben, akkor a nem ejektor szűrő algoritmusa nem realizált.

Ábra. 4.4. -lánc
Például fontolja meg a legegyszerűbb digitális szűrőt -cepi-hoz hasonló (4.4. Ábra). Impulzus jellemző -pontok
![]()
A megfelelő digitális szűrő impulzus-jellemzőjének rögzítéséhez a expresszióban ki kell cserélni, azonban a fedélzet impulzus jellemzője dimenzióval rendelkezik, és a digitális szűrő impulzus jellemzője méret nélkülinek kell lennie. Ezért csökkentjük a multiplikált a kifejezésben (4.2), és írjuk a digitális szűrő impulzus jellemzőjét
![]()
Az ilyen impulzus jellemző végtelenül sok tagot tartalmaz, de értékük csökken az exponenciális törvény, és csak a tagokra korlátozódik, így ezt választja
Most rögzítheti a szűrő kimenet kifejezését
Ez a kifejezés egyidejűleg a digitális szűrő algoritmus. A szűrő diagramja az 1. ábrán látható. 4.5.
A digitális szűrők folyamatainak elemzésének második megközelítése hasonló a hagyományos analóg áramkörök elemzési módszeréhez, csak a laptóz-átalakítás-átalakítás helyett.

Ábra. 4.5. A nem-ejtő digitális szűrő rendszere hasonló a -KEP-hez
Határozza meg a digitális szűrő paramétert, hasonlóan az elektromos áram átviteli funkciójához. Ehhez alkalmazza - feldolgozza a digitális szűrő impulzus jellemzőjére:

A funkciót a szűrő rendszerfunkciójának nevezik.
Összhangban a kifejezést (4.1), a jel a digitális szűrő kimenet egyenlő egy diszkrét konvolúció a bemeneti jel, és a szűrő impulzus jellemző. Ehhez az expresszióhoz képest a tétel-konvertálás, akkor kapjuk meg, hogy a kimeneti jel konverziója megegyezik a bemeneti jel átalakításával, szorozva a szűrőrendszer funkcióval:
![]()
Így a rendszerfunkció a digitális szűrő átviteli funkciójának szerepét játssza le.
Például megtaláljuk az első rendű digitális szűrő rendszerfunkcióját, hasonlóan a -cepi:

A jelek áthaladásának a digitális szűrőkön keresztül történő elemzésének harmadik módja hasonló a differenciálegyenletek klasszikus módszeréhez. Tekintsük ezt a módszert a soros áramkör példájára.
Az 1. sorrend legegyszerűbb analóg lánca a - (lásd 4.4 ábra), a jelek áthaladása, amelyen keresztül a differenciálegyenlet írja le
![]()
A különálló egyenlet helyett (4.8) helyett különbséget kell rögzíteni, ahol a bemeneti és kimeneti jelek diszkrét pillanatokra és a származék helyett a diszkrét pillanatokra vannak beállítva, a szomszédos jelértékek különbsége . Az 1. sorrend diszkrét láncára a különbségegyenletet meglehetősen általános formában rögzíthetjük.
Alkalmazza a konverziós egyenletre
ahol megtalálja a szűrő rendszerfunkcióját
![]()
A (4.10) képlet meglehetősen gyakori expresszió az 1. sorrend digitális szűrő rendszerének funkciójához. Amikor egybeesik a korábban kapott expressziót (4.7) egy digitális szűrő rendszerfunkciójához, ami egyenértékű -ci.
Megtaláljuk a rendszerfunkciónak megfelelő digitális szűrő algoritmust (4.10). E célból a (4.9) egyenlethez viszonyítva
Az algoritmus egyenértékű sémáját az 1. ábrán mutatjuk be. 4.6. A nem-neurisztikus szűrőhöz képest (lásd 4.5 ábra) itt adtunk hozzá egy különös "visszajelzési láncot", ami azt jelenti, hogy a kimeneti értékeket az alábbiakban használják

Ábra. 4.6. Rekurzív digitális szűrő rendszere, amely hasonló a -cepi-hoz
számítások. Ez a típusú szűrők rekurzív.
Az algoritmus (4.11) megfelel a szűrőnek, amely teljesen megfelel az előzőleg nem E-szűrőnek. De ahhoz, hogy meghatározzuk egy értéket a kimeneti jel segítségével nem ejective szűrő (4.4) algoritmus (4.4), műveletre van szükség, és ha a rekurzív szűrő algoritmus (4,11), csak két művelet. Ez a rekurzív szűrők fő előnye. Ezenkívül a rekurzív szűrők lehetővé teszik a nagyobb pontossággal rendelkező jel feldolgozását, mivel lehetővé teszik, hogy jobban beilleszkedjen egy impulzus-jellemzőt a "farok" elismerése nélkül. Rekurzív szűrők lehetővé teszik az algoritmusok végrehajtását, általában nem rendszerezett szűrők alkalmazásával. Például egy szűrővel, amely az 1. ábra szerint működik. 4.6, lényegében egy ideális meghajtó-integrátor és egy impulzus jellemző forma egy szűrő ilyen tulajdonság egy nem szisztémás rendszert nem lehet végrehajtani.
A figyelembe vett példák azt mutatják, hogy nincs értelme alkalmazni a nem ejtő algoritmusokat a digitális szűrők létrehozására egy nagy hosszúságú pulzáló jellemzőkkel. Ezekben az esetekben célszerűbb rekurzív szűrők használata.
A nem szisztémás algoritmusok hatóköre a digitális szűrők impulzusos jellemzővel, amely kis számú tagot tartalmaz. A példa a legegyszerűbb differenciálódás, amelynek jele, amelynek kimenete megegyezik a bemeneti jel növekményével:
Az ilyen digitális szűrő diagramját az 1. ábrán mutatjuk be. 4.7.

Ábra. 4.7. A legegyszerűbb digitális különbség rendszere
Fontolja meg most egy közös formájú digitális szűrőt, amelyet az egyenlet írja le
Ez az egyenlet különbségi egyenletnek és digitális szűrő algoritmusnak tekinthető, ha egyébként átírja, nevezetesen

Ábra. 4.8. A rekurzív digitális forma szűrő rendszere
Az algoritmus (4.13) megfelel az 1. ábrán bemutatott ábrán látható diagramnak. 4.8. Keresse meg az ilyen szűrő rendszerfunkcióját. Ehhez alkalmazzuk az átalakítási egyenletre:
A kifejezés (4.14) lehetővé teszi, hogy linket hozzon létre a szűrőáramkörök láncai és a rendszer funkció között. A rendszerfunkciós számok együtthatók meghatározzák az együtthatók értékeit
(A szűrő nem keresztmetszete részében), és a denominátorban lévő együtthatók határozzák meg a szűrő rekurzív részét.
48 Digitális szűrők véges impulzus jellemzővel. KIH szűrők kiszámítása.
Szűrő véges impulzus jellemzővel (Nem idegi szűrő, KIH szűrő) vagy FIR szűrő (FIR Socre. véges Impulse Response - véges impulzus jellemző) - az egyik típusú lineáris digitális szűrők, jellemző tulajdonsága, amely a korlátozott ideig annak hajtóimpuizusának (néhány alkalommal válik pontosan nullára ). Az ilyen szűrőt a visszajelzés hiánya miatt nem neurisztikusnak nevezik. Az ilyen szűrő átviteli funkciójának nevezője bizonyos állandó.
A szűrő bemeneti és kimeneti jelei közötti kapcsolatot leíró különbség egyenlet: ahol P.- a szűrő sorrendje, x.(n.) - bemenet, y.(n.) - kimeneti jel, és b. ÉN. - Szűrő együtthatók. Más szóval, a kimeneti jel bármely referenciájának értékét a skálázott értékek összege határozza meg. P.korábbi minták. Másik egyébként megmondhatod: A szűrő kimeneti értékét bármikor a bemenet pillanatnyi értékére adott válasz értéke és az összes fokozatosan leeső válasz összege P.előző jelminták, amelyek még mindig befolyásolják a kimenetet (után) P.- az impulzus átmeneti funkció áramlása nulla lesz, amint azt már említettük, így az összes tag után P.-HO is egyenlő lesz nulla). Az előző egyenletet több tartályba írjuk:

Annak érdekében, hogy megtaláljuk a szűrő magját
x.(n.) = δ( n.)
ahol δ ( n.) - Delta funkció. Ezután a KIH szűrő impulzus jellemzője rögzíthető:

Az impulzus jellemző Z-átalakítása megadja a QIH szűrő átviteli funkcióját:

] Tulajdonságok
A KIH szűrő számos hasznos tulajdonsággal rendelkezik, amelyek miatt néha előnyösebben használható, mint egy BIA szűrő. Itt van néhány közülük:
A KIH szűrők stabilak.
A kivitel során KIH szűrők nem igényelnek visszajelzést.
Fázisú kIH szűrők lineárisak lehetnek
Közvetlen szűrőforma
A szűrők három elem segítségével valósíthatók meg: szorzó, adder és késleltetési egység. Az ábrán látható változat az 1. típusú KIH szűrők közvetlen megvalósítása.

A szűrő közvetlen formájának végrehajtása
Példa Program
Az alábbiakban egy példa a C-ben írt KIH szűrőprogramra:
/ * Szűrő 128 csapra * /
float fir_filter (úszó bemenet)
statikus float minta;
acc \u003d 0,0f; /* Akkumulátor */
/ * Szorzás felhalmozódással * /
mert (i \u003d 0; i< 128; i++) {
aCC + \u003d (H [I] * minta [i]);
/* Kimenet */
/ * A késleltetési jel eltolása * /
mert (i \u003d 127, i\u003e 0, én--)
minta [i] \u003d minta;
49 Az adatok simítása. Csúszó átlagolás.
50 adat simítás. A parabolami simítás.
51 Adat simítás. Spencer simítás.
52 Az adatok simítása. Mediai szűrés.
Csúszó átlagolás, simítás az utazásokkal, simítás Spencer, medián szűrés
Amikor módszerek kidolgozása paramétereinek meghatározására fizikai folyamatok, lassan változik az időben, egy fontos feladata, hogy megszüntesse a hatását zajhatások vagy véletlenszerű zavarok, amelyek nyugszanak a feldolgozható jelet kapott kimenetén az elsődleges átalakító.
Az ilyen hatás kiküszöböléséhez adatokat alkalmazhat. Az ilyen simítás egyik legegyszerűbb módja az aritmetikai átlagolás. Amikor alkalmazzák, a diszkrét funkció (adat feldolgozható) értékét a kifejezésnek megfelelően kell kiszámítani:
hol - az aritmetikai átlagolás (páratlan egész szám) pontjai száma;
A feldolgozás előtti értékfüggvény;
Egyéb, meglehetősen hatékony módja a simítás, például a második fokú parabolami öt, hét, kilenc és tizenegy pontban a kifejezéseknek megfelelően:
vagy parabolami negyedik fokozat hét, kilenc, tizenegy és tizenhárom pont:
Gyakorlati alkalmazásokban más hatékony módszerek, például a Spencer 15 pontos simítása, jó eredményeket adnak:
Ezeknek a kifejezéseknek a helyettesítése a komplex kiállítóhoz, ahol egy sebességváltó funkciót és nem megfelelő konverziót határozhat meg.
Az aritmetikai átlagoláshoz
A zárójelben lévő kifejezés a denominátor geometriai progressziója, ezért ez a kifejezés ábrázolható:
 .
.
Ez a képlet az alacsony frekvenciájú szűrő átviteli jellemzője, és látható, hogy minél nagyobb az összetevők vesznek részt az átlagolásban, annál nagyobb a jele a zaj nagyfrekvenciás komponensei a jelben (lásd a 6.1 ábrát).
Azonban az ideiglenes tendenciák feldolgozásában bekövetkező frekvencia szemantikai koncepciója eltér a hasonló koncepciótól a jelek feldolgozása során. Ezt azzal magyarázza, hogy az ideiglenes tendenciák tanulmányozása során az érdeklődés nem a frekvenciaösszetételük, hanem a változás típusa (növekedés, csökkenés, állandóság, ciklikusság stb.).
Ez is meglehetősen hatékonyan az adatok simításához. Alkalmazás, úgynevezett heurisztikus algoritmusok.
Az egyikük mediánszűrés. A dimenzióval rendelkező csúszó ideiglenes ablakban egy kis páratlan számú, a központi elemet a központi elemet a szekvencia átlagos eleme váltja fel, amelyet a növekvő értékek sorrendje, a simított jel adatsorának elemei az időablakban. Az előnye, hogy a medián szűrés képes eltávolítani impulzus interferencia időtartama nem haladja meg, szinte torzítás nélkül simán változó jeleket. A zaj elnyomásának módja nem rendelkezik szigorú matematikai igazolással, de a számítások egyszerűsége és a kapott eredmények hatékonysága széles körben elterjedt.

6.1 ábra - Gate Charts
az aritmetikai átlagolás m \u003d 5, 7, 9, 11
Egy másik érdekes simító algoritmus a medián átlagolás. A lényege a következő. A csúszó idő ablakban a dimenzió (- teljes páratlan szám), az adatgyűjtő elemei növekvő sorrendben vannak megrendelésre, majd a megrendelt sorrendből az akadémiai és utolsó elemek eltávolításra kerülnek a megrendelt sorrendből.<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как
Ez a módszer lehetővé teszi az impulzus és a rádiófrekvenciás interferencia elnyomását, valamint a jelek jó simítását.
| " |