1st year, higher mathematics, we study matrices and basic actions on them. Here we systematize the main operations that can be performed with matrices. Where to start acquaintance with matrices? Of course, from the simplest things - definitions, basic concepts and simplest operations. We assure that the matrices will be understood by everyone who devotes at least a little time to them!
Definition of a matrix
Matrix Is a rectangular table of elements. Well, in simple terms - a table of numbers.
Usually matrices are indicated by uppercase Latin letters. For example, the matrix A , matrix B etc. Matrices can be of different sizes: rectangular, square, there are also row matrices and column matrices, called vectors. The size of the matrix is \u200b\u200bdetermined by the number of rows and columns. For example, let's write a rectangular matrix of size m on n where m - the number of lines, and n - the number of columns.
Elements for which i \u003d j (a11, a22, .. ) form the main diagonal of the matrix, and are called diagonal.
What can you do with matrices? Add / subtract, multiply by a number, multiply among themselves, transpose... Now about all these basic operations on matrices in order.
Matrix addition and subtraction operations
We warn you right away that you can only add matrices of the same size. The result is a matrix of the same size. Adding (or subtracting) matrices is easy - just add their respective elements ... Let's give an example. Let's add two matrices A and B, two by two.
Subtraction is performed by analogy, only with the opposite sign.
Any matrix can be multiplied by an arbitrary number. To do this, you need to multiply each of its elements by this number. For example, let's multiply the matrix A from the first example by the number 5:
Matrix multiplication operation
Not all matrices can be multiplied among themselves. For example, we have two matrices - A and B. They can be multiplied by each other only if the number of columns of matrix A is equal to the number of rows of matrix B. In this case each element of the resulting matrix, standing in the i-th row and j-th column, will be equal to the sum of the products of the corresponding elements in the i-th row of the first factor and the j-th column of the second... To understand this algorithm, let's write down how two square matrices are multiplied:
And an example with real numbers. Let's multiply matrices:
Matrix transpose operation
Matrix transpose is an operation where the corresponding rows and columns are swapped. For example, let's transpose the matrix A from the first example:
Matrix determinant
Determinant, but determinant is one of the basic concepts of linear algebra. Once upon a time, people invented linear equations, and behind them they had to invent a determinant. As a result, you have to deal with all this, so, the last spurt!
A determinant is a numerical characteristic of a square matrix, which is needed to solve many problems.
To calculate the determinant of the simplest square matrix, you need to calculate the difference between the products of the elements of the main and secondary diagonals.
The determinant of a matrix of the first order, that is, consisting of one element, is equal to this element.
What if the matrix is \u200b\u200bthree by three? This is more complicated, but you can cope.
For such a matrix, the value of the determinant is equal to the sum of the products of the elements of the main diagonal and the products of elements lying on triangles with an edge parallel to the main diagonal, from which the product of the elements of the secondary diagonal and the product of elements lying on the triangles with an edge of the parallel secondary diagonal are subtracted.
Fortunately, it is rarely necessary to calculate determinants of large matrices in practice.
Here we have covered the basic operations on matrices. Of course, in real life you can never even come across a hint of a matrix system of equations, or vice versa - to face much more difficult cases when you really have to break your head. It is for such cases that there is a professional student service. Ask for help, get a high-quality and detailed solution, enjoy your academic success and free time.
This manual will help you learn how to perform operations with matrices: addition (subtraction) of matrices, transposition of a matrix, multiplication of matrices, finding the inverse matrix. All material is presented in a simple and accessible form, corresponding examples are given, so even an unprepared person can learn how to perform actions with matrices. For self-checking and self-checking, you can download a matrix calculator for free \u003e\u003e\u003e.
I will try to minimize theoretical calculations, in some places explanations “on the fingers” and the use of unscientific terms are possible. Lovers of solid theory, please do not criticize, our task is learn to perform actions with matrices.
For SUPERFAST preparation on the topic (who is "on fire") there is an intensive pdf-course Matrix, determinant and test!
A matrix is \u200b\u200ba rectangular table of any elements... As elements we will consider numbers, that is, numeric matrices. ELEMENT Is a term. It is desirable to remember the term, it will be often encountered, it is not by chance that I used bold type to highlight it.
Designation: matrices are usually denoted by uppercase Latin letters
Example: Consider a two-by-three matrix:
This matrix consists of six elements:
All numbers (elements) inside the matrix exist by themselves, that is, there is no question of any subtraction: 
It's just a table (set) of numbers!
We will also agree do not rearrange numbers, unless otherwise stated in the explanations. Each number has its own location and cannot be shuffled!
The matrix in question has two rows: 
and three columns: 
STANDARD: when talking about the size of the matrix, then first indicate the number of rows, and only then - the number of columns. We have just taken apart a two-by-three matrix.
If the number of rows and columns of the matrix is \u200b\u200bthe same, then the matrix is \u200b\u200bcalled square, eg: 
- "three by three" matrix.
If the matrix has one column or one row, then such matrices are also called vectors.
In fact, we know the concept of a matrix since school, consider, for example, a point with coordinates "x" and "game":. Essentially, the coordinates of a point are written in a one-by-two matrix. By the way, here's an example for you why the order of numbers matters: and are two completely different points of the plane.
Now let's go directly to the study actions with matrices:
1) First action. Removing the minus from the matrix (adding the minus to the matrix).
Back to our matrix 
... As you may have noticed, there are too many negative numbers in this matrix. This is very inconvenient from the point of view of performing various actions with the matrix, it is inconvenient to write so many minuses, and it just looks ugly in design.
Move the minus out of the matrix, changing the sign of EACH matrix element:
At zero, as you understand, the sign does not change, zero - it is zero in Africa.
Reverse example: 
... It looks ugly.
Let's add a minus to the matrix by changing the sign of EACH matrix element:
Well, it turned out much nicer. And, most importantly, it will be EASIER to perform any actions with the matrix. Because there is such a mathematical folk omen: the more cons, the more confusion and mistakes.
2) Second action. Matrix multiplication by number.
Example:
It's simple, in order to multiply a matrix by a number, you need each the element of the matrix is \u200b\u200bmultiplied by the given number. In this case, the top three.
Another useful example:
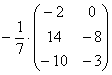- matrix multiplication by a fraction
First, consider what to do DO NOT:
It is NOT NECESSARY to enter a fraction into the matrix, firstly, it only complicates further actions with the matrix, and secondly, it makes it difficult for the teacher to check the solution (especially if 
- the final answer of the task).
And especially, DO NOT divide each element of the matrix by minus seven:
From article Math for dummies or where to start, we remember that decimal fractions with a comma in higher mathematics are tried in every possible way to avoid.
The only thing desirable to do in this example is to introduce a minus into the matrix:
But if ALL matrix elements were divisible by 7 without residue, then it would be possible (and necessary!) to divide.
Example:
In this case, you can and NEED TO multiply all elements of the matrix by, since all the numbers in the matrix are divisible by 2 without residue.
Note: in the theory of higher mathematics there is no school concept of "division". Instead of the phrase "divide this by this" you can always say "multiply this by a fraction." That is, division is a special case of multiplication.
3) Third action. Matrix Transpose.
In order to transpose a matrix, you need to write its rows into the columns of the transposed matrix.
Example:
Transpose Matrix
There is only one line here and, according to the rule, it must be written to a column:
- transposed matrix.
A transposed matrix is \u200b\u200busually indicated by a superscript or a top-right stroke.
Step by step example:
Transpose Matrix 
First, we rewrite the first row to the first column:
Then we rewrite the second line into the second column: 
Finally, we rewrite the third line into the third column:
Done. Roughly speaking, to transpose means to turn the matrix to one side.
4) Action four. Sum (difference) of matrices.
The sum of matrices is a simple operation.
NOT ALL MATRIX CAN BE FOLDED. To perform the addition (subtraction) of matrices, it is necessary that they are the same in size.
For example, if a two-by-two matrix is \u200b\u200bgiven, then it can only be added with a two-by-two matrix and no other! 
Example:
Add matrices 
and 
In order to add matrices, it is necessary to add their corresponding elements:
For the difference of matrices, the rule is similar, it is necessary to find the difference of the corresponding elements.
Example:
Find the difference of matrices 
, 
And how to solve this example easier so as not to get confused? It is advisable to get rid of unnecessary minuses, for this we add a minus to the matrix:
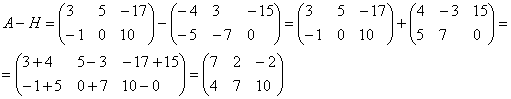
Note: in the theory of higher mathematics there is no school concept of "subtraction". Instead of saying "subtract this from this" you can always say "add a negative number to this." That is, subtraction is a special case of addition.
5) Action five. Matrix multiplication.
What matrices can be multiplied?
For a matrix to be multiplied by a matrix, you need so that the number of columns of the matrix is \u200b\u200bequal to the number of rows of the matrix.
Example:
Is it possible to multiply a matrix by a matrix?
This means that you can multiply these matrices.
But if the matrices are rearranged, then, in this case, multiplication is already impossible!
Therefore, multiplication is not possible:
It is not uncommon to find tasks with a trick, when a student is asked to multiply matrices, the multiplication of which is obviously impossible.
It should be noted that in a number of cases it is possible to multiply matrices either way.
For example, for matrices, and both multiplication and multiplication are possible
Matrix multiplication by number is an operation on a matrix, as a result of which each of its elements is multiplied by a real or complex number. It looks like this in mathematical language:
$$ B \u003d \\ lambda \\ cdot A \\ Rightarrow b_ (ij) \u003d \\ lambda a_ (ij) $$
It is worth noting that the resulting matrix $ B $ should result in the same dimension as the initial matrix $ A $. You can also pay attention to the following fact: $ \\ lambda \\ cdot A \u003d A \\ cdot \\ lambda $, that is, you can swap the multipliers and this will not change the product.
It will be useful to use the operation of multiplying a matrix by a number when moving the common factor outside the matrix. In this case, each element of the matrix is \u200b\u200bdivided by the number $ \\ lambda $, and it is taken out in front of the matrix.
Properties
- Distributive law for matrices: $$ \\ lambda \\ cdot (A + B) \u003d \\ lambda A + \\ lambda B $$ Multiplication of the sum of matrices by a number can be replaced by the sum of the products of each individual matrix by a given number
- Distributive law for real (complex) numbers: $$ (\\ lambda + \\ mu) \\ cdot A \u003d \\ lambda A + \\ mu A $$ Multiplication of a matrix by the sum of numbers can be replaced by the sum of the products of each number by the matrix
- Associative law: $$ \\ lambda \\ cdot (\\ mu \\ cdot A) \u003d (\\ lambda \\ cdot \\ mu) A $$ It is convenient to use if you need to take the common factor out of the matrix in front of it, while multiplying the coefficient already in front of it
- There is a special number $ \\ lambda \u003d 1 $, due to which the matrix remains unchanged $$ 1 \\ cdot A \u003d A \\ cdot 1 \u003d A $$
- Multiplying a matrix by zero leads to the fact that each element of the matrices is zeroed and the matrix becomes zero of the same dimension that it was originally: $$ 0 \\ cdot A \u003d 0 $$
Solution examples
| Example |
| Given $ A \u003d \\ begin (pmatrix) 2 & -1 & 4 \\\\ 0 & 9 & 3 \\\\ - 2 & -3 & 5 \\ end (pmatrix) $ and real $ \\ lambda \u003d 2 $. Multiply number by matrix. |
| Decision |
|
We write down the mathematical operation of multiplication and at the same time remember the rule that says: the matrix is \u200b\u200bmultiplied by a number element by element. $$ \\ lambda \\ cdot A \u003d 2 \\ cdot \\ begin (pmatrix) 2 & -1 & 4 \\\\ 0 & 9 & 3 \\\\ - 2 & -3 & 5 \\ end (pmatrix) \u003d \\ begin (pmatrix) 2 \\ cdot 2 & 2 \\ cdot (-1) & 2 \\ cdot 4 \\\\ 2 \\ cdot 0 & 2 \\ cdot 9 & 2 \\ cdot 3 \\\\ 2 \\ cdot (-2) & 2 \\ cdot (-3) & 2 \\ cdot 5 \\ end (pmatrix) \u003d $$ $$ \u003d \\ begin (pmatrix) 4 & -2 & 8 \\\\ 0 & 18 & 6 \\\\ - 4 & -6 & 10 \\ end (pmatrix) $$ As a result, we see that each number in the matrix has doubled in relation to the initial value. If you can't solve your problem, then send it to us. We will provide a detailed solution. You will be able to familiarize yourself with the course of the calculation and get information. This will help you get credit from the teacher in a timely manner! |
| Answer |
| $$ \\ lambda \\ cdot A \u003d \\ begin (pmatrix) 4 & -2 & 8 \\\\ 0 & 18 & 6 \\\\ - 4 & -6 & 10 \\ end (pmatrix) $$ |
In order to multiply the matrix A by an arbitrary number α, you need the elements of the matrix A multiply by the number α, i.e. the matrix-number product will be as follows:
Example 1. Find Matrix 3 Afor matrix
Decision. In accordance with the definition, we multiply the elements of the matrix A by 3 and get
It was a very simple example of multiplying a matrix by a number with integers. There are also simple examples ahead, but already such where among the factors and elements of matrices there are fractions, variables (letter designations), because the laws of multiplication apply not only for integers, so it is never harmful to repeat them.
Example 2. A by the number α if 
,
.
A by α, not forgetting that when multiplying fractions, the numerator of the first fraction is multiplied by the numerator of the first fraction and the product is written into the numerator, and the denominator of the first fraction is multiplied by the denominator of the second fraction and the product is written into the denominator. When receiving the second element of the first row of the new matrix, the resulting fraction was reduced by 2, this must be done. We get
Example 3. Perform matrix multiplication operation A by the number α if
,
.
Decision. Multiply the elements of the matrix A by α, without getting confused in the letter notation, not forgetting to leave a minus in front of the second element of the second row of the new matrix, and remembering that the result of multiplying a number by its inverse number is one (the first element of the third row). We get
.
Example 4. Perform matrix multiplication operation A by the number α if 
,
.
Decision. Remember that when you multiply a number in a power by a number in a power, the exponents are added. We get
.
This example, among other things, clearly demonstrates that the operations of multiplying a matrix by a number can be read (and written) in reverse order, and this is called putting a constant factor in front of the matrix.
Combined with addition and subtraction of matrices the operation of multiplying a matrix by a number can form various matrix expressions, for example, 5 A − 3B , 4A + 2B .
Properties of multiplying a matrix by a number
(here A, B - matrices, - numbers, 1 - number one)
1. 
2. 
3. 
Properties (1) and (2) connect the multiplication of a matrix by a number with the addition of matrices. There is also a very important connection between multiplying a matrix by a number and multiplying the matrices themselves:
that is, if in the product of matrices one of the factors is multiplied by a number, then the entire product will be multiplied by a number.
This topic will cover such operations as addition and subtraction of matrices, matrix multiplication by a number, matrix multiplication by matrix, matrix transposition. All symbols used on this page are taken from the previous topic.
Addition and subtraction of matrices.
The sum $ A + B $ of matrices $ A_ (m \\ times n) \u003d (a_ (ij)) $ and $ B_ (m \\ times n) \u003d (b_ (ij)) $ is called the matrix $ C_ (m \\ times n) \u003d (c_ (ij)) $, where $ c_ (ij) \u003d a_ (ij) + b_ (ij) $ for all $ i \u003d \\ overline (1, m) $ and $ j \u003d \\ overline (1, n) $.
A similar definition is introduced for the difference of matrices:
The difference $ AB $ of matrices $ A_ (m \\ times n) \u003d (a_ (ij)) $ and $ B_ (m \\ times n) \u003d (b_ (ij)) $ is the matrix $ C_ (m \\ times n) \u003d ( c_ (ij)) $, where $ c_ (ij) \u003d a_ (ij) -b_ (ij) $ for all $ i \u003d \\ overline (1, m) $ and $ j \u003d \\ overline (1, n) $.
Explanation of the entry $ i \u003d \\ overline (1, m) $: show \\ hide
The notation "$ i \u003d \\ overline (1, m) $" means that the $ i $ parameter ranges from 1 to m. For example, the record $ i \u003d \\ overline (1,5) $ says that the $ i $ parameter takes the values \u200b\u200b1, 2, 3, 4, 5.
It is worth noting that addition and subtraction operations are defined only for matrices of the same size. In general, addition and subtraction of matrices are intuitively clear operations, because they mean, in fact, just the addition or subtraction of the corresponding elements.
Example # 1
Three matrices are given:
$$ A \u003d \\ left (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) \\; \\; B \u003d \\ left (\\ begin (array) (ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 \\ end (array) \\ right); \\; \\; F \u003d \\ left (\\ begin (array) (cc) 1 & 0 \\\\ -5 & 4 \\ end (array) \\ right). $$
Can you find the $ A + F $ matrix? Find matrices $ C $ and $ D $ if $ C \u003d A + B $ and $ D \u003d A-B $.
The $ A $ matrix contains 2 rows and 3 columns (in other words, the size of the $ A $ matrix is \u200b\u200b$ 2 \\ times 3 $), and the $ F $ matrix contains 2 rows and 2 columns. The sizes of the matrix $ A $ and $ F $ do not coincide, so we cannot add them, i.e. the $ A + F $ operation for the given matrices is undefined.
The sizes of the matrices $ A $ and $ B $ are the same, i.e. the matrix data contains an equal number of rows and columns, so the addition operation is applicable to them.
$$ C \u003d A + B \u003d \\ left (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) + \\ left (\\ begin (array ) (ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 \\ end (array) \\ right) \u003d \\\\ \u003d \\ left (\\ begin (array) (ccc) -1 + 10 & -2+ ( -25) & 1 + 98 \\\\ 5 + 3 & 9 + 0 & -8 + (- 14) \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (array) \\ right) $$
Find the matrix $ D \u003d A-B $:
$$ D \u003d AB \u003d \\ left (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) - \\ left (\\ begin (array) ( ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 \\ end (array) \\ right) \u003d \\\\ \u003d \\ left (\\ begin (array) (ccc) -1-10 & -2 - (- 25 ) & 1-98 \\\\ 5-3 & 9-0 & -8 - (- 14) \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (ccc) -11 & 23 & -97 \\ : $ C \u003d \\ left (\\ begin (array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (array) \\ right) $, $ D \u003d \\ left (\\ begin (array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ end (array) \\ right) $.
AnswerMultiplying a matrix by a number.
The product of the matrix $ A_ (m \\ times n) \u003d (a_ (ij)) $ by the number $ \\ alpha $ is the matrix $ B_ (m \\ times n) \u003d (b_ (ij)) $, where $ b_ (ij) \u003d \\ alpha \\ cdot a_ (ij) $ for all $ i \u003d \\ overline (1, m) $ and $ j \u003d \\ overline (1, n) $.
Simply put, multiplying a matrix by a certain number means multiplying each element of a given matrix by that number.
Example No. 2
The matrix is \u200b\u200bgiven: $ A \u003d \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) $. Find the matrices $ 3 \\ cdot A $, $ -5 \\ cdot A $ and $ -A $.
{!LANG-987d634ed94c15a31370f162c6a7a9ca!}
$$ 3 \\ cdot A \u003d 3 \\ cdot \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) \u003d \\ left (\\ begin ( array) (ccc) 3 \\ cdot (-1) & 3 \\ cdot (-2) & 3 \\ cdot 7 \\\\ 3 \\ cdot 4 & 3 \\ cdot 9 & 3 \\ cdot 0 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (ccc) -3 & -6 & 21 \\\\ 12 & 27 & 0 \\ end (array) \\ right). \\\\ -5 \\ cdot A \u003d -5 \\ cdot \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (ccc) -5 \\ cdot (-1) & - 5 \\ cdot (-2) & -5 \\ cdot 7 \\\\ -5 \\ cdot 4 & -5 \\ cdot 9 & -5 \\ cdot 0 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) ( ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ end (array) \\ right). $$
The $ -A $ notation is a shorthand for $ -1 \\ cdot A $. That is, to find $ -A $, you need to multiply all the elements of the $ A $ matrix by (-1). In fact, this means that the sign of all elements of the matrix $ A $ will change to the opposite:
$$ -A \u003d -1 \\ cdot A \u003d -1 \\ cdot \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) \u003d \\ : $ 3 \\ cdot A \u003d \\ left (\\ begin (array) (ccc) -3 & -6 & 21 \\\\ 12 & 27 & 0 \\ end (array) \\ right); \\; -5 \\ cdot A \u003d \\ left (\\ begin (array) (ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ end (array) \\ right); \\; -A \u003d \\ left (\\ begin (array) (ccc) 1 & 2 & -7 \\\\ -4 & -9 & 0 \\ end (array) \\ right) $.
AnswerProduct of two matrices.
The definition of this operation is cumbersome and, at first glance, incomprehensible. Therefore, first I will indicate a general definition, and then we will analyze in detail what it means and how to work with it.
The product of the matrix $ A_ (m \\ times n) \u003d (a_ (ij)) $ by the matrix $ B_ (n \\ times k) \u003d (b_ (ij)) $ is the matrix $ C_ (m \\ times k) \u003d (c_ ( ij)) $, for which each element of $ c_ (ij) $ is equal to the sum of the products of the corresponding elements of the i-th row of the matrix $ A $ by the elements of the j-th column of the matrix $ B $: $$ c_ (ij) \u003d \\ sum \\ limits_ (p \u003d 1) ^ (n) a_ (ip) b_ (pj), \\; \\; i \u003d \\ overline (1, m), j \u003d \\ overline (1, n). $$
Let us analyze step-by-step matrix multiplication using an example. However, you should immediately pay attention that not all matrices can be multiplied. If we want to multiply the $ A $ matrix by the $ B $ matrix, then first we need to make sure that the number of columns of the $ A $ matrix is \u200b\u200bequal to the number of rows of the $ B $ matrix (such matrices are often called
agreed {!LANG-69f0e6da9be87b2fd3d70d6670655bd5!}). For example, the matrix $ A_ (5 \\ times 4) $ (the matrix contains 5 rows and 4 columns) cannot be multiplied by the matrix $ F_ (9 \\ times 8) $ (9 rows and 8 columns), since the number of columns of the matrix $ A $ is not equal to the number of rows in the $ F $ matrix, i.e. $ 4 \\ neq 9 $. But you can multiply the matrix $ A_ (5 \\ times 4) $ by the matrix $ B_ (4 \\ times 9) $, since the number of columns in the matrix $ A $ is equal to the number of rows in the matrix $ B $. In this case, the result of multiplying the matrices $ A_ (5 \\ times 4) $ and $ B_ (4 \\ times 9) $ will be the matrix $ C_ (5 \\ times 9) $, containing 5 rows and 9 columns:
Example No. 3
The matrices are given: $ A \u003d \\ left (\\ begin (array) (cccc) -1 & 2 & -3 & 0 \\\\ 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & -5 \\ end (array) \\ right) $ and $ B \u003d \\ left (\\ begin (array) (cc) -9 & 3 \\\\ 6 & 20 \\\\ 7 & 0 \\\\ 12 & -4 \\ end (array) \\ right) $. Find the matrix $ C \u003d A \\ cdot B $.
To begin with, let's immediately determine the size of the $ C $ matrix. Since the matrix $ A $ is $ 3 \\ times 4 $, and the matrix $ B $ is $ 4 \\ times 2 $, the size of the $ C $ matrix is: $ 3 \\ times 2 $:
So, as a result of the product of the matrices $ A $ and $ B $, we should get the matrix $ C $, consisting of three rows and two columns: $ C \u003d \\ left (\\ begin (array) (cc) c_ (11) & c_ ( 12) \\\\ c_ (21) & c_ (22) \\\\ c_ (31) & c_ (32) \\ end (array) \\ right) $. If the designations of the elements raise questions, then you can look at the previous topic: "Matrices. Types of matrices. Basic terms", at the beginning of which the designation of the matrix elements is explained. Our goal is to find the values \u200b\u200bof all elements of the matrix $ C $.
Let's start with $ c_ (11) $. To get the element $ c_ (11) $, you need to find the sum of the products of the elements of the first row of the matrix $ A $ and the first column of the matrix $ B $:
To find the element $ c_ (11) $ itself, you need to multiply the elements of the first row of the matrix $ A $ by the corresponding elements of the first column of the matrix $ B $, i.e. the first element to the first, the second to the second, the third to the third, the fourth to the fourth. We summarize the results obtained:
$$ c_ (11) \u003d - 1 \\ cdot (-9) +2 \\ cdot 6 + (- 3) \\ cdot 7 + 0 \\ cdot 12 \u003d 0. $$
Let's continue the solution and find $ c_ (12) $. To do this, you have to multiply the elements of the first row of the matrix $ A $ and the second column of the matrix $ B $:
Similar to the previous one, we have:
$$ c_ (12) \u003d - 1 \\ cdot 3 + 2 \\ cdot 20 + (- 3) \\ cdot 0 + 0 \\ cdot (-4) \u003d 37. $$
All elements of the first row of matrix $ C $ are found. Move on to the second line, which begins with $ c_ (21) $. To find it, you have to multiply the elements of the second row of the matrix $ A $ and the first column of the matrix $ B $:
$$ c_ (21) \u003d 5 \\ cdot (-9) +4 \\ cdot 6 + (- 2) \\ cdot 7 + 1 \\ cdot 12 \u003d -23. $$
The next element $ c_ (22) $ is found by multiplying the elements of the second row of the matrix $ A $ by the corresponding elements of the second column of the matrix $ B $:
$$ c_ (22) \u003d 5 \\ cdot 3 + 4 \\ cdot 20 + (- 2) \\ cdot 0 + 1 \\ cdot (-4) \u003d 91. $$
To find $ c_ (31) $ we multiply the elements of the third row of the matrix $ A $ by the elements of the first column of the matrix $ B $:
$$ c_ (31) \u003d - 8 \\ cdot (-9) +11 \\ cdot 6 + (- 10) \\ cdot 7 + (-5) \\ cdot 12 \u003d 8. $$
And, finally, to find the element $ c_ (32) $, you have to multiply the elements of the third row of the matrix $ A $ by the corresponding elements of the second column of the matrix $ B $:
$$ c_ (32) \u003d - 8 \\ cdot 3 + 11 \\ cdot 20 + (- 10) \\ cdot 0 + (-5) \\ cdot (-4) \u003d 216. $$
All elements of the matrix $ C $ are found, it remains only to write that $ C \u003d \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right) $ ... Or, to write in full:
$$ C \u003d A \\ cdot B \u003d \\ left (\\ begin (array) (cccc) -1 & 2 & -3 & 0 \\\\ 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & - 5 \\ end (array) \\ right) \\ cdot \\ left (\\ begin (array) (cc) -9 & 3 \\\\ 6 & 20 \\\\ 7 & 0 \\\\ 12 & -4 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right). $$
Answer: $ C \u003d \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right) $.
By the way, there is often no reason to describe in detail the finding of each element of the result matrix. For matrices whose size is small, you can do the following:
$$ \\ left (\\ begin (array) (cc) 6 & 3 \\\\ -17 & -2 \\ end (array) \\ right) \\ cdot \\ left (\\ begin (array) (cc) 4 & 9 \\\\ - 6 & 90 \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (cc) 6 \\ cdot (4) +3 \\ cdot (-6) & 6 \\ cdot (9) +3 \\ cdot (90 ) \\\\ -17 \\ cdot (4) + (- 2) \\ cdot (-6) & -17 \\ cdot (9) + (- 2) \\ cdot (90) \\ end (array) \\ right) \u003d \\ left (\\ begin (array) (cc) 6 & 324 \\\\ -56 & -333 \\ end (array) \\ right) $$
It is also worth noting that matrix multiplication is non-commutative. This means that in general $ A \\ cdot B \\ neq B \\ cdot A $. Only for some types of matrices that are called permutation (or commuting), the equality $ A \\ cdot B \u003d B \\ cdot A $ is true. It is on the basis of the non-commutativity of multiplication that it is required to indicate exactly how we multiply the expression by this or that matrix: to the right or to the left. For example, the phrase "multiply both sides of the equality $ 3E-F \u003d Y $ by the matrix $ A $ on the right" means that we need to obtain the following equality: $ (3E-F) \\ cdot A \u003d Y \\ cdot A $.
Transposed with respect to the matrix $ A_ (m \\ times n) \u003d (a_ (ij)) $ is called the matrix $ A_ (n \\ times m) ^ (T) \u003d (a_ (ij) ^ (T)) $, for elements which $ a_ (ij) ^ (T) \u003d a_ (ji) $.
Simply put, in order to get the transposed matrix $ A ^ T $, you need to replace the columns in the original matrix $ A $ with the corresponding rows according to the following principle: if the first row was, the first column will become; there was a second line - the second column will become; there was a third line - there will be a third column and so on. For example, let's find the transposed matrix to the matrix $ A_ (3 \\ times 5) $:
Accordingly, if the original matrix was $ 3 \\ times 5 $, then the transposed matrix is \u200b\u200b$ 5 \\ times 3 $.
Some properties of operations on matrices.
It is assumed here that $ \\ alpha $, $ \\ beta $ are some numbers, and $ A $, $ B $, $ C $ are matrices. For the first four properties, I indicated the names, the rest can be named by analogy with the first four.
